Lesson 3 Part 1 Locally weighted regression
局部加权紧接着上面的线性回归中参数求解来继续讲吧。还是以上面的房屋价格的预测,它的中心思想是在对参数进行求解的过程中,每个样本对当前参数值的影响是有不一样的权重的。比如上节中我们的回归方程为(这个地方用矩阵的方法来表示Ɵ表示参数,i表示第i个样本,h为在Ɵ参数下的预测值):
我们的目标是让
最小,然后求出来Ɵ,再代入h中就可以得到回归方程了。
但是如果类似以下的样本,他们的对应图如下:

如果用之前的方法,图中线为求出的回归方程,那么在x的取值和真实差别很大,这个情况叫做欠拟合。那么我们怎么办呢?我们的主要思想就是只对x的附近的一些样本进行选择,根据这些样本得到x附近这些样本所推倒出来的回归方程,那么此时我们得到的回归方程就比较拟合样本数据,得到的效果图如下:
我们解的思路如下,加入一个加权因子:
重新构造新的j(x)
Exp是以e为底的指数,这个时候可以知道如果x距离样本很远的时候w(i)=0,否则为1,当我们预测一个值的时候就需要我们重新来计算当前的参数Ɵ的值,然后构造回归方程,计算当前的预测值。
这就是局部加权回归LWR!
τ控制了权值随距离下降的速率
看下我们的matlab程序吧
clc; clear; close all; load datax.dat; load datay.dat; X = [ones(size(datax, 1),1) datax]; Y = datay; m = size(X,1); n = size(X,2)-1; %part a figure(1); hold on; theta = inv(X'*X)*X'*Y; scatter (X(:,2), Y); Xp = -6:0.01:13; Yp = theta(1) + theta(2)*Xp; plot (Xp, Yp); %part b figure(2); hold on; W = zeros(m); t = 0.8; LWRXp = -6:0.01:13; LWRYp = []; for temp = 1:size(LWRXp,2), for i=1:m, W(i,i) = 0.5 * exp(-((LWRXp(temp)-X(i,2))^2)/(2*t*t)); end; theta = inv(X'*W*X)*X'*W*Y; LWRYp(temp) = theta(1)+theta(2)*LWRXp(temp); end; scatter (X(:,2), Y); plot (LWRXp, LWRYp); %part c figure(3); hold on; scatter (X(:,2), Y); W = zeros(m); t_array = [0.1, 0.3, 2,10]; LWRXp = -6:0.01:13; LWRYp = []; for t=1:4, for temp = 1:size(LWRXp,2), for i=1:m, W(i,i) = 0.5 * exp(-((LWRXp(temp)-X(i,2))^2)/(2*t_array(t)*t_array(t))); end; theta = inv(X'*W*X)*X'*W*Y; LWRYp(t,temp) = theta(1)+theta(2)*LWRXp(temp); end; end; plot (LWRXp, LWRYp);
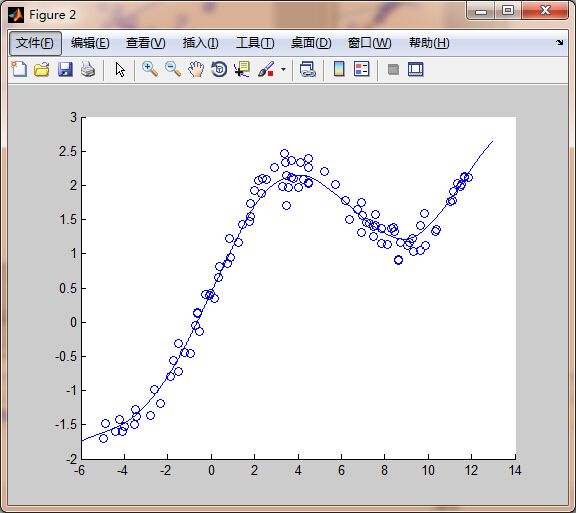
part a的结果就是最小二乘的线性拟合
part b 中 t = 0.8
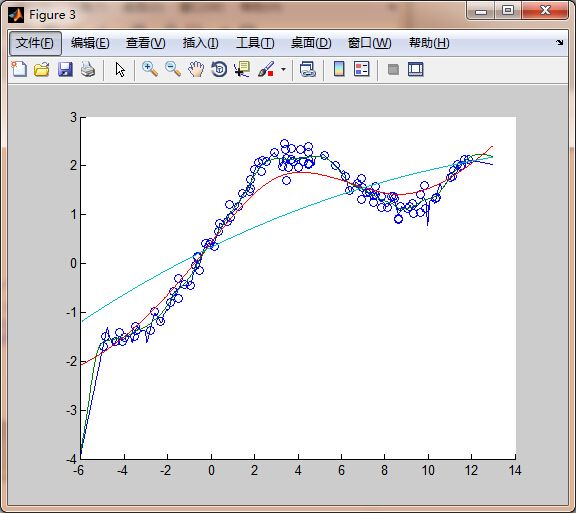
part c用了几种不同的t