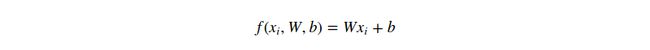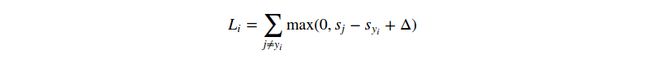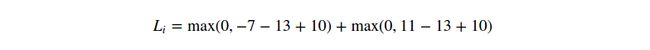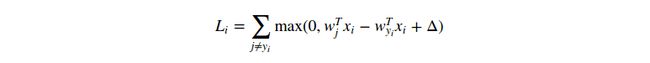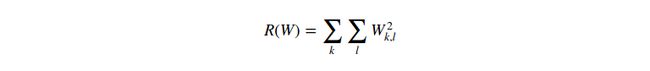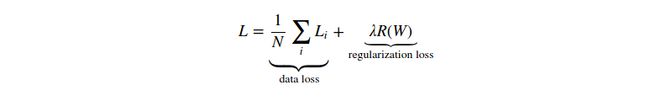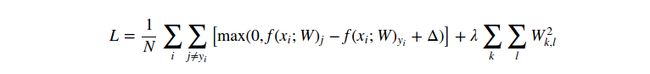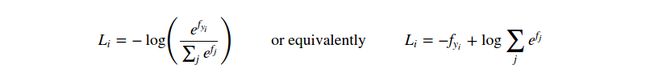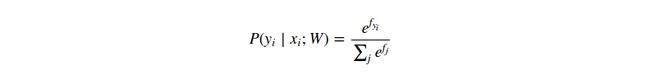Linear Classification: Support Vector Machine, Softmax
原文地址：http://cs231n.github.io/linear-classify/
＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃
内容列表：
１．介绍线性分类器
２．线性成绩函数
３．解释一个线性分类器
４．损失函数
4.1．多类支持向量机
4.2 . Softmax分类器
4.3 . 支持向量机 vs Softmax
５．线性分类器的交互式web例子
６．总结
###############################################3
Linear Classification
上节讲了图像分类的问题，即为一张测试图像用一组训练类别中选择一个类别的任务。另外，我们还描述了最近邻（kNN）分类器，它是通过比较测试图像和训练集图像（已标记）之间的远近关系来判断测试图像类别的。可以看到，最近邻（kNN）分类器有如下缺点：
１）为了和测试数据的比较，分类器必须存储所有训练集数据。这对于存储空间来说是很浪费的，因为数据集可能会很大。
２）因为测试图像需要通过和所有训练图像的比较才能分类，所以在计算上很耗费时间。
Overview. 现在，我们将要开发一个对图像分类更有效的分类器，最后，我们将很自然的扩展到整个神经网络和卷积神经网络。这个分类器主要有两个部分：一个是成绩函数（score function）：通过它我们可以将原始数据转换为对于类的成绩值；另一个是损失函数（loss function）：用于量化预测的图像类别和该测试图像真正类别之间的差异程度。我们将会把这个作为最优化问题，相对于成绩函数的参数来尽量减小损失函数的值。
Parameterized mapping from images to label scores
该分类器的第一个部分就是定义一个成绩函数，用于转换图像像素值到该测试图像相对于每个类的置信度。我们将通过具体的案例来开发这个方法。和往常一样，先假定一个图像训练集
，每一张训练图像都与一个标记（类别）
相对应，其中
，
。因此，我们共有N张训练图像（每张共有D维）以及K个不同的类别。例如，在CIFAR-10上我们共有训练集N=5,000张图像，每张图像有D=32x32x3=3072个像素点，类别数K=10，因此共有10个不同类别（狗，猫，车等）。现在，我们定义成绩函数为
，用于转换原始图像像素值到类成绩。
Linear classifier. 在这个模块，我们从一个最简单的函数开始，这是一个线性匹配函数：
在上面的等式中，我们假定图像
的所有像素点被拉伸为一列向量，大小为[Dx1]。矩阵W（大小为[KxD]）和向量b（大小为[Kx1]）均为函数的参数。在CIFAR-10上，
表示第i个图像的所有像素点拉伸后的一列向量（大小为[3072x1]），W大小为[10x3072]，b大小为[10x1]，所以共有3072个值输入本函数，最终输出10个数字（表示测试图像相对于每类的成绩）。W中的参数经常被称为权重，b也经常被称为偏置向量，因为b虽然影响输出成绩，但没有和实际输入数据
进行交互。所以，经常把术语权重和参数互换使用。
几点注意：
１）单矩阵乘法
表示并行使用10个独立的分类器进行评估（每一类一个），每一个类别就是W的一行参数。
２）输入数据
是固定不变的，但我们可以改变参数W，b的值。我们的目标是设置好参数，使得计算出来的结果和整个训练集的真正类别相匹配。下面会有更详细的讲解关于如何做，但是直观上我们希望匹配正确类别的成绩比匹配不正确类别的成绩高。
３）该分类器的优势是训练数据可以仅用于训练。一旦训练完成后就可以舍弃整个训练集数据而仅保留已学习的参数值。因为测试图像可以仅通过这个分类器函数进行计算，基于得到的成绩就能分类。
４）最后，分类一个测试图像包括一个矩阵乘法以及一个加法，这和之前的比较整个训练集图像相比在速度上有很大的提高。
Interpreting a linera classifier
一个线性分类器计算一张测试图像的成绩是通过加权求和该测试图像3个颜色通道上所有的像素值而得到的。通过权重值的设定，分类器可以“喜欢”或“不喜欢”（依靠每个权重值的符号）图像上某个具体位置的某种颜色。比如，一个图片的边缘部分有许多蓝色，那么它更可能属于“船”的类别（也可能是“水”的类别）。你可以预计到，“船”分类器在蓝色通道上有很多符号为正的权重值（如果存在蓝色就能增加“船”类别的成绩），以及在红／绿通道上有很多负的权重值（出现红色／绿色则会减小“船”类别的成绩）。
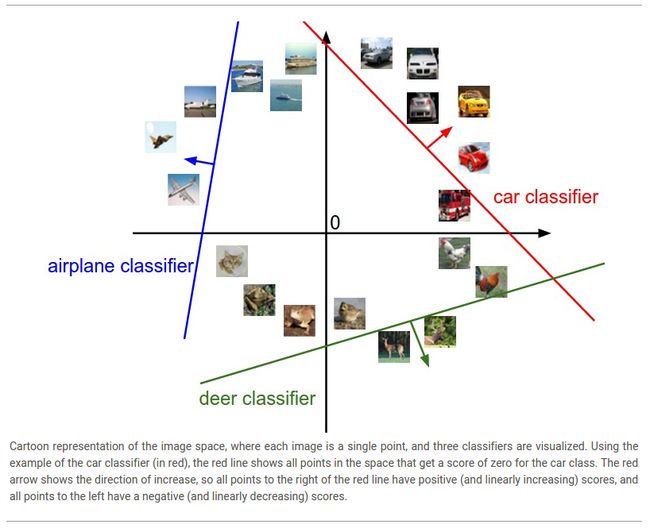
Analogy of images as high-dimensional points. 因为图像被拉伸为一个高维列向量，所以我们可以将每一幅图片看作一个高维空间上的点（比如，CIFAR-10上的图像共有32x32x3=3072个像素，所以可以看出一个3072维空间里的一个点）。类似地，整个数据集就是一组（已标记类别）的点。
因为我们将每一类的成绩都定义为图像所有像素点的加权求和的值，所以每一个类分类器就是该空间上的一个线性函数。虽然我们无法可视化3072维的空间，但如果我们将这些维度定义为2维，那么可视化结果如下：
正如前面所说的，权重矩阵W的每一行就是一个类的分类器。几何解释如下：如果我们改变了W的某一行数据，那么在像素空间中的对应行将会转换到不同的方向。另一方面，偏执向量b可以改变分类器的位置。如果没有b，那么不论W如何，当
时总会得到成绩为０，因为此时所有行都通过原点。
Interpretation of linear classifies as template matching. 权值W的另一种解释就是W的每一行都是一个类的模板（有时也称为蓝本）。一张测试图像相对于每个类别的成绩可以在测试图像和对应类别的模板上使用点积操作获得，从中比较出最好的成绩就是该测试图像的类别。所以线性分类器其实是在进行模板匹配，而这些模板是可以通过学习得到的。另一种思考的方式是我们仍然是在进行最近邻分类，只不过并没有使用所有训练图像，而是每各类仅使用一个模板（模板可以通过学习得到，并且不一定是训练集中已有的图像），并且我们使用（负的）点积操作来代替L1/L2距离操作。
另外，注意到马的模板好像有一只双头马，这是由于数据集中有面向左边的马和面向右边的马。线性分类器整合了这两种马的模式到一个模板上。类似的，车的模板看起来也整合了多种不同的模式到一个模板上，这样，不得不从四面八方，不同颜色来识别。并且，这个模板呈现红色，隐含了在CIFAR-10数据集中有更多的红颜色的车子。由于线性分类器性能太弱，无法正确识别不同颜色的车，但之后的神经网络能够完成这个任务。超前一步：神经网络能够在隐藏层开发中间神经元，可以检测指定的车的类型（比如，面向左边的绿色的车，面向前面的蓝色的车等），并且下一层的神经元通过一个独立的车检测器的加权求和将这些结合成一个更加精确的成绩。
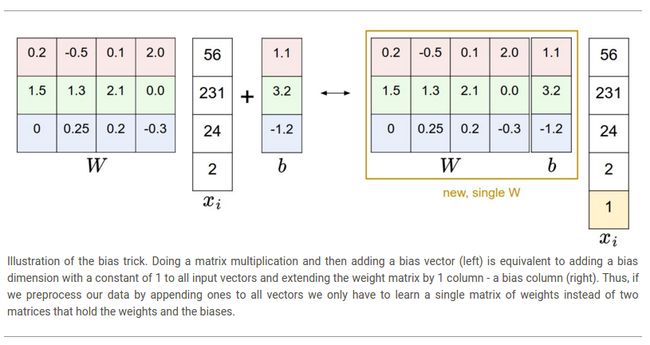
Bias trick. 在继续下面学习之前，我们想要提及一个通用的简化技巧，就是把两个参数W,b转换为一个。之前定义的成绩函数如下：
按照上述格式进行处理略微有些麻烦，因为必须分开保存两组参数（偏置向量b和权值矩阵W）。一个通用的技巧是把两组参数合并在一个矩阵里，即扩展向量
，使其多一维，并且该维默认值为常量１－一个默认偏执维。有了这个额外的一维，新的成绩函数可以简化为一个矩阵乘法：
在CIFAR-10中，
的大小从[3072x1]变为[3073x1]－（额外的一维拥有常量１），权重W的大小由[10x3072]变为[10x3073]。W中额外的一列表示偏置向量b。如下所示：
Image data preprocessing. 在上面的例子中，我们使用原始像素值（范围在[0 ... 255]之间）进行操作。在机器学习中，常用方法是执行输入特征的归一化（在图像案例中，每一个像素被认为是一个特征）。并且，每一个特征的零均值也是很重要的。在图像案例中，这相当于在从训练图像中计算出一个均值图像，然后每个图像都减去这个均值图像，从而使得其像素分布近似为[-127 ... 127]。更进一步的操作是缩放每一个特征使得其取值范围为[-1, 1]。综合上面的方法，零均值中心化可能是更加重要的，在学习理解梯度下降的动态理论后我们才能理解其原因。
Loss function
上一节我们定义了一个函数，用于转换像素值为类的成绩，该函数通过一组权重W来参数化。另外，我们无法改变输入数据
（它们是固定的），但我们可以改变权重值。目的是通过设置权重值，使得在训练数据中预测的类的成绩和正确的结果是一致的。
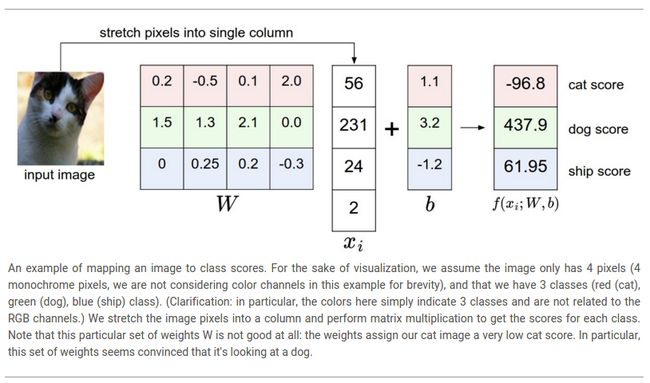
举个例子，之前讲过的检测一只猫的例子，其检测类别为“猫”，“狗”和“船”。可以看到这个例子的记过并不理想：像素描绘的是猫但是“猫”类别的成绩很低（-96.8）而其他类别的成绩很高（“狗”：437.9；“船”：61.95）。我们想要通过一个损失函数（aloss function, or sometimes also referred to as thecost function or theobjective）来衡量我们对于输出结果的满意程度。直观上来说，如果结果不满意，损失函数值应该很高；相反，损失函数值应该很低。
Multiclass Support Vector Machine loss
有好几种定义损失函数的方式。首先我们将要开发一种常用的方法，称为多类支持向量机损失（the Multiclass Support Vector Machhine(SVM) loss）函数。支持向量机损失函数创建的目的是，支持向量机想要在一个固定的间隔
内，每张图像的正确类别的成绩比不正确的类别成绩更高。有时可以把损失函数理解成之前的内容：支持向量机想要好的结果的损失函数值更低。
更详细的说明。回忆之前的第i个例子，我们给予了图像
的像素值以及类别
，然后指定正确类别的下标。成绩函数（score function）得到了像素值然后计算类别成绩
，我们简称为s（成绩的简称）。比如，第j个类别的成绩就是第j个元素：
。第i个例子的多类支持向量机损失函数可以归纳如下：
Example. 让我们用一个例子来看看上述公式是如何操作的。假设我们有3个类别，得到的成绩为
，并且第一个类是正确的类别。并且假定
（一个超参数，将会在后面详细说明）的值为10。用上述公司来求和不正确的类别，可以得到两个子项：
可以看到，第一个子项结果为0，因为[-7-13+10]的结果为负，而阈值函数
的阈值为0，所以结果为0。我们在这一个子项得到结果0，因为正确的类别成绩（１３）比不正确的类别成绩(-7)更大，超过了区间值10。事实上差值为20，但支持向量机仅仅关心10以内的差值；任何超过区间值的差值均赋值为0。第2个子项计算结果为[11-13+10]=8。虽然正确类别的成绩比不正确类别的成绩更高（13>11），但没有超过区间值10，所以输出损失值为8。结果就是，支持向量机损失函数想要正确类别的成绩比任何不正确类别的成绩大，并且至少超过区间值
（delta），否则将会累加损失值。
注意，在上述模块我们使用的是线性成绩函数
，所以我们也可以重写损失函数的格式如下：
其中，
是权重W的第j行。一旦我们改变的成绩函数f的格式，那么上述公式也就无法使用。
在解释本小节之前，我们还将提到一个术语，那就是0阈值函数
，也被称为thehinge loss。有时候还会使用the squared hinge loss（或者叫L2-SVM）来代替，其函数格式为
，that penalizes violated margins more strongly(quadratically instead of linearly)。未平方的标准是更加标准的，但在有些数据集中，使用squared hinge loss有更好的效果。可以通过交叉验证决定。
Regularization. 上面提到的损失函数有一个缺陷。假设我们有一个数据集和一组参数W，使用参数W可以正确分类数据集中的所有图片（即所有的正确分类的成绩都比不正确分类的成绩高，并且高于区间值，所以
）。问题是这组权重值W得到的结果并不是独一无二的：可能还有其他类似的权重值W能够正确分类所有图像（也就是所有图像的损失值为0）。一个简单的验证方法就是如果权重W可以正确分类，假设
，那么权重
也可以正确的分类所有图像，因为这种改变同时拉伸了所有成绩的量级，因此它们的绝对差异同样拉伸了同样量级。举个例子，如果一个正确类别和它最相近的类别之间的差值是15，那么权重W乘以参数2后，新的差值将变为30。
换句话说，我们希望编码一组特定的权重来消除上面的模糊性。我们可以用一个regulariation penalty
来扩展损失函数。最常用的regularization penalty是L2格式，它通过一个基于所有参数的二次惩罚来阻止更大的权重：
在上面的表达式中，我们将会求和所有的参数值的平方。注意，规则化函数并不是作用于数据的，它仅作用于权重。完整的多类支持向量机包括了规则化惩罚函数，所以公狗两个部分：数据损失（thedata loss：基于所有图像的损失值
的平均）和规则化损失（theregularization loss）。格式如下：
或者是扩展格式：
其中N是训练样本的数目。如图所示，我们在损失函数中添加了规则惩罚函数，其权重为一个超参数
。没有简单的方式来设置这个超参数，通过是通过交叉编译来决定的。
将规则化惩罚添加进来会有很多可取得特性，除了我们上面提到的，还有许多我们将会在下节讲解。比如，事实证明拥有了L2格式惩罚后，在支持向量机上会出现最大边距（max margin，如果想要了解更多细节，可以查看CS229的课程笔记）。
每吸引人的特性就是它惩罚了大的权重趋向，有助于提高泛化能力，因为它意味着没有输入维度可仅凭本身就能在最终成绩上获得大的影响。举个例子，假设我们有输入向量
，以及两个权重向量
和
。并且
，所以这两个权重向量和输入数据的点积结果相同，但是权重向量
的L2格式的惩罚是1.0，而权重向量
的L2格式惩罚仅为0.25。所以，相对于L2格式惩罚来说，权重向量
更好，因为它的规则化损失值更低。直观上来说，这是因为权重向量
更小而且更diffuse。因为L2格式惩罚更喜欢更小和更diffuse的权重向量，the final classifier is encouraged to take into account all input dimensions to small amounts rather than a few input dimensions and very strongly。本节后面我们将会看到，它可以提高分类器的泛化性能，可以减小过拟合。
注意，偏置值没有相同的影响，不像权重值，它们无法控制一个输入维度的影响强度。因此，经常只规则化权重W，而不规则化偏置b。然而，在实际中，产生的影响几乎忽略不计。最后，注意由于规则化惩罚的影响，我们无法在所有样本上都实现0损失，仅在W=0的情况下才能出现。
Code. 下面是Python下的损失函数（不含规则化）的实现，有两个版本，非矢量化和矢量化格式：
def L_i(x, y, W):
"""
unvectorized version. Compute the multiclass svm loss for a single example (x,y)
- x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)
with an appended bias dimension in the 3073-rd position (i.e. bias trick)
- y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)
- W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)
"""
delta = 1.0 # see notes about delta later in this section
scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
correct_class_score = scores[y]
D = W.shape[0] # number of classes, e.g. 10
loss_i = 0.0
for j in xrange(D): # iterate over all wrong classes
if j == y:
# skip for the true class to only loop over incorrect classes
continue
# accumulate loss for the i-th example
loss_i += max(0, scores[j] - correct_class_score + delta)
return loss_i
def L_i_vectorized(x, y, W):
"""
A faster half-vectorized implementation. half-vectorized
refers to the fact that for a single example the implementation contains
no for loops, but there is still one loop over the examples (outside this function)
"""
delta = 1.0
scores = W.dot(x)
# compute the margins for all classes in one vector operation
margins = np.maximum(0, scores - scores[y] + delta)
# on y-th position scores[y] - scores[y] canceled and gave delta. We want
# to ignore the y-th position and only consider margin on max wrong class
margins[y] = 0
loss_i = np.sum(margins)
return loss_i
def L(X, y, W):
"""
fully-vectorized implementation :
- X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
- y is array of integers specifying correct class (e.g. 50,000-D array)
- W are weights (e.g. 10 x 3073)
"""
# evaluate loss over all examples in X without using any for loops
# left as exercise to reader in the assignment本节的内容就是支持向量机损失函数采用一种特殊的方法来衡量训练数据的预测结果如何与真正的类别相一致。另外，在训练数据上有一个好的预测结果也等价于将损失减小到最低程度。
Practical Considerations
Setting Delta. 让我们温习一下超参数
以及它的设置。我们应该给它设定什么值？需要交叉验证吗？事实证明这个超参数可以在所有例子中都安全的设为1.0（
）。超参数
和
看起来好像是两个不同的值，但是实际上，它们两个都控制了相同的权衡（they both control the same tradeoff）：在损失函数中数据损失和规则化损失之间的权衡（The tradeoff between the data loss and the regularization loss in the objective）。理解这个的关键在与权重W的量级是直接影响成绩的（包括它们的差值）：当我们减小W的所有权重值时，相应的成绩之间的差值会变得更低；当我们提高了权重，那么成绩差值会变得更大。因此，边距（margin）的确切值（比如，
或者
）看起来是无意义的，因为权重W可以任意的拉伸和缩减差值。所以，唯一真正的权衡就是我们允许权重多大（通过规则化强度
）。
Relation to Binary Support Vector Machine. 在上这门课之前，你可能会有一些关于二类支持向量机的经验，第i个样本的损失函数格式如下：
其中，C是一个超参数，
。不用担心，上述格式其实是我们现在提出的公式的一个特例，当仅需进行２类划分的时候的格式。也就是说，当我们仅需进行２类划分的时候，其损失函数可以简化为上述格式。同时，这个格式的超参数
和我们的格式中的超参数
控制着相同的权衡，其关系为倒数关系
。
Aside：Optimization in primal. 如果你之前学习过有关SVM的知识，那么你可能听过这些术语：核心（kernels），duals，the SMO 算法等。In this class （as is the case with Neural Networks in general）we will always work with the optimization objectives in their unconstrained form. Many of these objectives are technically not differentiable (e.g. the max(x,y) function isn't because it has a kink when x=y), but in practice this is not a problem and it is common to use a subgradient.
Aside: Other Multiclass SVM formulations. It is worth noting that the Multiclass SVM presented in this section is one of few ways of formulating the SVM over multiple classes. Another commonly used form is the One-Vs-All (OVA) SVM which trains an independent binary SVM for each class vs. all other classes. Related, but less common to see in practice is also the All-vs-All (AVA) strategy. Our formulation follows the Weston and Watkins 1999 (pdf) version, which is a more powerful version than OVA (in the sense that you can construct multiclass datasets where this version can achieve zero data loss, but OVA cannot. See details in the paper if interested). The last formulation you may see is a Structured SVM, which maximizes the margin between the score of the correct class and the score of the highest-scoring incorrect runner-up class. Understanding the differences between these formulations is outside of the scope of the class. The version presented in these notes is a safe bet to use in practice, but the arguably simplest OVA strategy is likely to work just as well (as also argued by Rikin et al. 2004 in In Defense of One-Vs-All Classification (pdf)).
Softmax classifier
事实证明SVM是常用的两种分类方法之一。另一个常见的分类器是the Softmax classifier（分类器），它拥有一个不同的损失函数。如果你之前听说过两类逻辑回归分类器，那么Softmax分类器就是它泛化到多类的形式。Softmax分类器给予一个略微直观的输出（归一化类别概率），有一个概率性的解释，我们之后将会提到。在Softmax分类器中，函数
并没有改变，但现在我们可以把这些成绩解释为每一个类的未归一化的逻辑概率，然后用一个交叉熵损失（cross-entropy loss）来代替hinge loss：
在这里我们使用符号
来表示类成绩向量
的第j个元素。和之前一样，完整的损失函数格式是整个训练集的
的均值加上一个规则化惩罚
。函数
称为softmax function（函数）：它得到一组成绩向量（记为
），然后归一化这组向量值，使得向量中的每一个值都在0和1之间，并且向量中的全部值求和为１。完整的交叉熵损失函数包括这个softmax函数。
Information theory view. 在真正的分布
和估计的分布
之间的交叉熵定义如下：
Softmax分类器因此最小化了估计的类概率分布（如前面所示
）和真正分布之间的交叉熵，which in this interpretation is the distribution where all probability mass is on the correct class（i.e. 
contains a single 1 at the 
-th position.）。Moreover, since the cross-entropy can be written in terms of entropy and the Kullback-Leibler divergence as 
, and the entropy of the delta function 
is zero, this is also equivalent to minimizing the KL divergence between the two distributions (a measure of distance). In other words, the cross-entropy objective wants the predicted distribution to have all of its mass on the correct answer.
Probabilistic interpretation. 表达式如下：
这个函数功能为得出图像
属于某一类别
的（归一化）概率，并且通过权重
参数化。To see this, remember that the Softmax classifier interprets the scores inside the output vector f as the unnormalized log probabilities. Exponentiating these quantities therefore gives the (unnormalized) probabilities, and the division performs the normalization so that the probabilities sum to one. In the probabilistic interpretation, we are therefore minimizing the negative log likelihood of the correct class, which can be interpreted as performing Maximum Likelihood Estimation (MLE). A nice feature of this view is that we can now also interpret the regularization term R(W)R(W) in the full loss function as coming from a Gaussian prior over the weight matrix WW, where instead of MLE we are performing the Maximum a posteriori (MAP) estimation. We mention these interpretations to help your intuitions, but the full details of this derivation are beyond the scope of this class.
Practical issues: Numeric stability. 当你在实际生活中编写代码计算Softmax分类器时，由于指数（the exponentials）的关系，中间术语（the intermediate terms）
和
可能会变得很大。除以大的数字可能会变得数字不稳定，所以使用一个归一化技巧是很重要的。如果我们同时在分子和分母上乘以一个常熟C and push it into the sum，我们将得到下面的（数字上是等价的）表达式：
我们可以任意选择C的值，因为这并不会改变结果，但我们可以通过使用这个值来提高计算的数值稳定性（the numerical stability）。常用C的值是
。This simply states that we should shift the values inside the vector 
so that the highest value is zero. 代码如下：
f = np.array([123, 456, 789]) # example with 3 classes and each having large scores p = np.exp(f) / np.sum(np.exp(f)) # Bad: Numeric problem, potential blowup # instead: first shift the values of f so that the highest number is 0: f -= np.max(f) # f becomes [-666, -333, 0] p = np.exp(f) / np.sum(np.exp(f)) # safe to do, gives the correct answer
SVM vs. Softmax
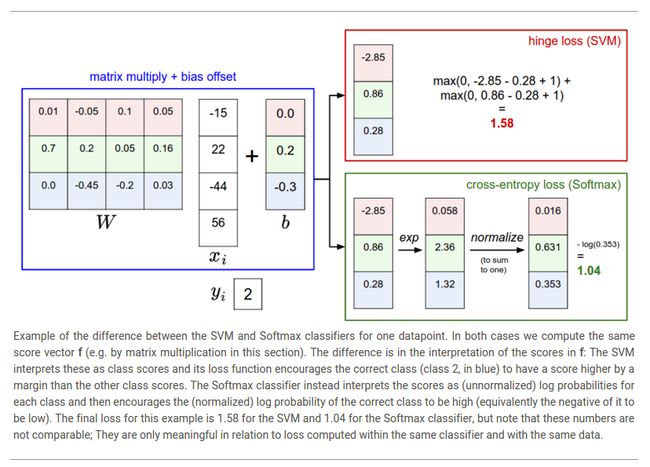
下图可能可以帮助理解Softmax和SVM分类器之间的不同：
Softmax classifier provides "probabilities" for each class. 不像SVM分类器那样computes uncalibrated 并且不容易去解释每个类的成绩，Softmax分类器允许我们去计算每一个可能类别的概率。举个例子，给予一张图片，使用SVM分类器得到成绩为
，分别对应于类别“猫”，“狗”和“船”。然后Softmax分类器计算这三个类别的概率为
这样你就能够直观了解它们分别属于哪个类别的概率。然而，我们使用“概率”这个术语的原因因为它严重依赖于规则化强度
－which you are in charge of as input to the system。举个例子，假设未归一化的逻辑概率为
。那么softmax函数计算如下：
执行的步骤是先进行指数操作，然后归一化。现在，如果规则化强度
更大，那么权重W会因此而变得更小。举个例子，假设权重变为一半
。那么计算如下：
where the probabilities are now more diffuse. 此外，在极限情况下，由于非常高的规则化强度
，那么权重可能会变得非常小，此时输出概率可能会相同。Hence, the probabilities computed by the Softmax classifier are better thought of as confidences where, similar to the SVM, the ordering of the scores is interpretable, but the absolute numbers (or their differences) technically are not.
In practice, SVM and Softmax are usually comparable. 在SVM和Softmax分类器之间的性能差异是非常小的，不同的人对此会有不同的见解。与Softmax分类器相比，SVM分类器 is a more local objective, which could be though of either as a bug or a feature. 比如，给予一个类别成绩
，然后第一个类是正确的。对于SVM分类器来说（e.g. with desired margin of 
），由于正确类别的成绩比其他类别都高，而且已经超出边距，所以会计算得出损失值为0。SVM分类器对于不同成绩的细节并不关心：比如成绩变为
，SVM分类器的损失值还是为0，因为正确类别的成绩比其他类别都高，而且已经超出了边距。但对于Softmax分类器来说并不如此，当成绩为
时，它的损失值比成绩为
更高。换句话说，Softmax分类器永远不会对成绩值满意：正确类别的成绩越高，不正确的类别成绩越低，那么损失值越大。However, the SVM is happy once the margins are satisfied and it does not micromanage the exact scores beyond this constraint. 这可以直观的认为是一个特征：比如，“车”分类器可以更注意于如果分离“小车”和“货车”而不需要去关系“青蛙”类别，因为“青蛙”类别的成绩很低, and which likely cluster around a completely different side of the data cloud.
Interactive web demo
Summary
１）我们定义了一个成绩函数（score function），用于转换图像像素值到类别成绩（在本小节，我们使用线性函数，其依赖于权重W和偏置b）
２）与kNN分类器相比，参数化方法（parametric approach）的好处是一旦学习完参数后，就可以舍弃所有的训练数据。另外，预测一张测试图像的时间很短，因为它仅需和W执行一个矩阵乘法即可，而并不需要和每一张训练图像进行比较。
３）介绍了偏置技巧（the bias trick），可以让我们把偏置向量加入到权重矩阵中，这样仅需执行一个矩阵乘法即可
４）定义了一个损失函数（loss function，介绍了两种在线性分类器上通用的损失函数：the SVM and the Softmax）来衡量给定一组参数，计算得到的结果和真正的结果之间的一致性比较。同时我们发现，有一个好的预测同时也意味着有一个小的损失值。
现在，我们知道了一种可以用一组参数来匹配图像的方式，同时我们知道了两种用来衡量预测质量的损失函数。但是我们如何才能知道那组参数可以得到最好的（最低的）损失值？这个方式就是最优化（optimization），这也是下一节的主题。
Further Reading
１）Deep Learning using Linear Support Vector Machines from Charlie Tang 2013 presents some results claiming that the L2SVM outperforms Softmax.