Fibonacci（斐波那契）数列的递归与非递归实现 python

关于递归算法，可以参考这篇文章 汉诺塔 经典递归算法 in python

Fibonacci数列为：0、1、1、2、3、5、8、13、21......

数列第一项为0，第二项为1，从第三项开始，每一项为相邻前两项之和。

用递归的方法来定义：

• F(0) = 0 
• F(1) = 1
• F(n) = F(n-1) + F(n-2) , n>=2

用递归方法实现代码：

# python 3.4
x = int ( input ("输入一个数：") )
def fibonacci ( n ) :
	if n == 0 : 
		return 0
	elif n == 1 :
		return 1
	else :
		return fibonacci( n - 1 ) + fibonacci( n - 2 )
for i in range ( 0 , x ) :
	print(fibonacci(i))

用非递归方法实现代码： 

# python 3.4
x = int ( input ("输入一个数：") )
arr = [ 0, 1, 1 ]   #计算数组中任意一项，需要用到的变量不超过3个，因此只需要用一个长度为3的数组
for i in range(0 , x ):      
	print ( str(arr[i%3])+"   " )           #第n祥依次放在下标为n%3的数组中
	arr[i%3]=arr[(i+1)%3] + arr[(i+2)%3]    #将该数组看成一个循环链表，则每一项输出后，相应的位置用来放项数比它大3的值，而这个值就是数组的后两项想加

（其实只需要两个变量就ok了）

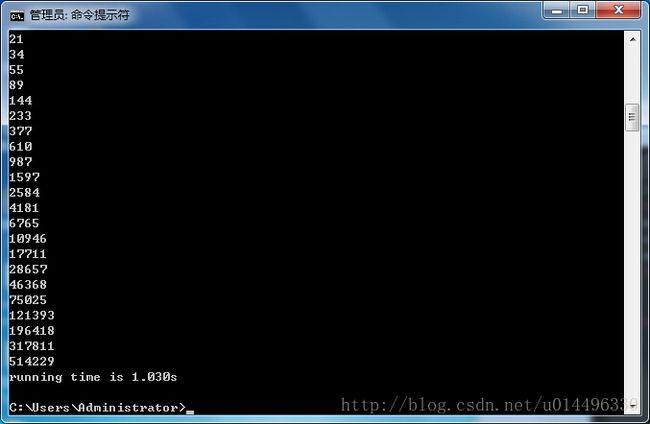
用递归方法程序清晰易懂，但是开销大。分别给两个程序加一个计时语句，看看n = 30 时两个程序运行时间相差多少。

修改后的代码：

# python 3.4
from time import clock
x = int ( input ("输入一个数：") )
clock()
def fibonacci ( n ) :
	if n == 0 :
		return 0
	elif n == 1 :
		return 1
	else :
		return fibonacci( n - 1 ) + fibonacci( n - 2 )
for i in range ( 0 , x ) :
	print(fibonacci(i))
print("running time is %-5.5ss" %clock())

# python 3.4
from time import clock
x = int ( input ("输入一个数：") )
clock()
arr = [ 0, 1, 1 ]   
for i in range(0 , x ):      
	print ( str(arr[i%3])+"   " )         
	arr[i%3]=arr[(i+1)%3] + arr[(i+2)%3]
print("running time is %-5.5ss" %clock())

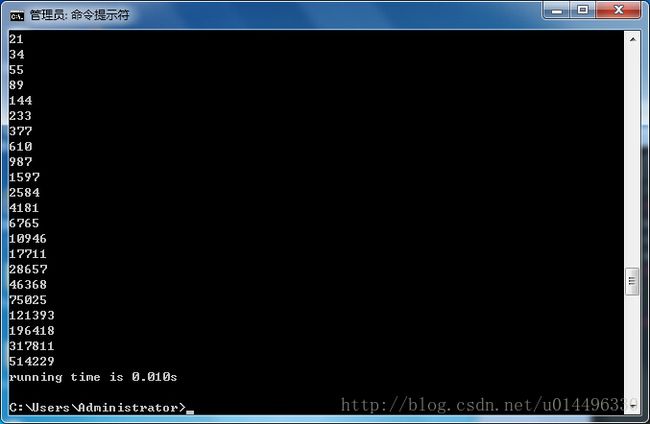
运行结果分别是：

递归方法求解：

非递归方法求解：