实验报告：运用shingling+minhash+lsh方法对文档相似性进行分析

实验报告

实验名称：文档相似性分析

一、实验目的

1．学习利用hadoop处理大数据。

2. 通过实验加强mapreduce编程能力。 

3. 进一步理解shingling+minhash+lsh方法。

 

二、实验内容

1．安装vmware、hadoop、centos操作系统。

2. 使用给定的数据集,完成对文档相似性分析的实验任务。

三、实验环境

centos操作系统、eclipse 

四、实验原理

4.1 shingling

在一堆非常多的文档中，找到相似的文档，或者对文档间的相似性进行评估。

当应用于此类目的的时候，我们最常用的用来表示一篇文档的方法是：shingling。

1. k-shingles

     可以把一篇文档看成一个字符串。那么一篇文档的k-shingle就是在这篇文档中出过现的任何长度为k的字符串。k-shingles就是该篇文档所有k-shingle的集合，在进行处理之前需要去掉文档中不必要的标点符号和多余的空格、换行。那么k的大小决定于什么因素呢？ 与文档的长度和所有的字符个数有关。k的取值一般要满足一个规则：k的取值应该能够满足，任何一个给定的shingle出现在任何给定的文档中的概率都非常低。一般对于邮件类的文档，k取值为5是最为合适的。假设在邮件中一般只会出现字母字符和空格字符。那么将会有27^5=14,348,907个可能的shingles。而一般的Email的字符长度会远小于14million。而在实际的测试中k=5也确实是表现的非常好。而对于长文档，如研究论文等k取9是一个安全的取值。

2. Hashing Shingles

     我们可以选择一个hash函数来将k-shingle映射成为数值，这样对文档的表示形式就是一群整数的集合。

4.2 保持相似度的集合摘要（MinHashing）

   可以发现，文档的shingles集合是非常大的，尽管我们用hash将其映射为4byte或者更大的整数。假设我们有上百万的文档，那么内存中就会放不下这些shingles的集合。

     我们的目标就是把大数据量的shingles集合变换为非常小的代表（称之为签名）。而且这样的签名应该有这样的性质： 能够很容易的对两个签名集合进行比较，并且能够较简单的计算两个签名集合的jaccard距离；而且，签名集合计算出来的的相似度（jaccard距离）应该和实际的相差不大，签名集合越大，越能接近准确值。

     MinHashing就是具有这些性质的获取签名的一种有效方法。 签名一般大概会取几百个左右，每一个值都是原代表集合的一个不同的MinHash值。

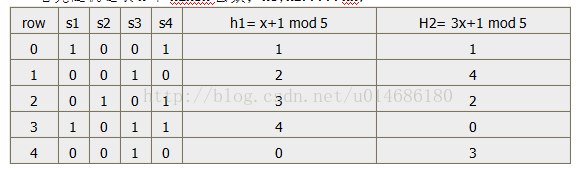
     那么如何计算一个集合的minhash值呢？ 首先，对集合的表示方法进行改变，假设现在三篇文档，我们用下面的方式来表示，称之为characteristic matrix; 左边的一列是所有出现过的元素。这样每一篇文档被表示为0,1集合。

同上，我们取几百个不同的minhash函数对矩阵进行不同的重排，就可以得到每个文档的签名（元素数目和所取得函数数目相同）  若要求一个文档的minhash值，首先对每一列的元素进行同样的重新排列，相当于把最左侧的element的顺序进行重排；然后，每一个文档的一个minhash值就是该列元素中第一’1‘所在位置的元素；（假设上表中就是已经重排后的矩阵，那么s1的该minhash值就是a， s2是c； s3是b；）

分析上边的计算过程，我们可以发现，在实际计算中，我们可以不用真的对所有元素进行重排（对于大数据量文档来说这是一个非常不现实的过程），因为我们只要找到第一个不元素1所在的位置就行了，所需要的只是按照minhash函数的规定一次遍历元素集直到知道元素1为止。

对于如何计算MinHash 签名，书上给出的是这样的方法： 由于对characteristic matrix的行（一般是百万甚至十亿级别的数量）进行重排是非常耗时的。所以我们通过hash函数来模拟重排过程，利用hash函数将行号映射到与行数相同的buckets中；hash的过程可能会有冲突，不过当k非常大而且冲突并不是非常多的时候区别并不是很大。

  首先随机选取n个hansh函数；h1,h2.....hn;

我们用SIG(i,c)用来存储第i个hash函数和第c列数据（文档c的变换表示）的签名值，并且初始化为无穷大。其次没我们对每一行r进行如下处理： 

    1.  计算 h1(r),h2(r)....hn(r);

   2.  对每一列c进行：  如果 c列r行的数值是0，什么也不做；  否则， 对每一个i=1,2,....n 设置SIG(i,c) = min(SIG(i,c), hi(r))；也就是设置为当前的SIG(i,c)值和hi(r)的最小值。 (过程相当于在计算的过程中，不断用重排后位置最靠前且数值为1的行号放在相应的SIG中，从而达到前文所述的求签名值得目的)

  通过上面的方法就可以求得一篇文档的minhan签名。但是尽管我们通过minhash将文档压缩为小的签名值，并且能保证相互间相似度的计算；我们仍不能很有效的找到相似度最高的文档对，因为要比较的文档数目可能非常大。这时候，如果我们的目标找到相似度在一定阈值以上的文档对，或者最相似的文档对；而不是计算所有的文档对的相似度，那么我们就可以采用LSH技术来简化计算。

4.3 LSH(Location Sensitive Hash)

通过上面一步得到的minhash的签名数量还是很大，在在线实时应用中，不可能去一一比较。LSH筛选出有极高相似概率的候选对，进而减少比较的次数。LSH要寻找一个哈希函数f(x,y)，它能够返回x，y是否是一个候选对。由于我们得到了签名矩阵，LSH就是将候选的列放到相同的Bucket中。

LSH选择一个相似度阀值s，如果两个列的签名相符度至少是s，那么就将它们放到同一个Bucket中。原理就这样简单，但是不是太粗糙了呢？

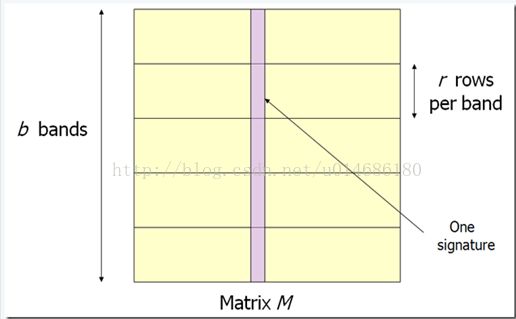
我们将矩阵的行分成b个Band（r行为一个Band）：

 

然后对每个Band做哈希，将她分区的列的一部分哈希到k个Bucket中。现在的候选对就是至少在1个Band中被哈希到同一个Bucket的列。分割之后的工作就是，调制参数b和r使尽可能可多的相似的对放到同一个Bucket，并且尽量减少不相似的对放到同一个Bucket中。

五、实验结果

5.1 Shingling

1.算出数据集总的shingle

先对数据集进行预处理，去掉文档中不必要的标点符号和多余的空格、换行，Shingle长度选择：5，总的shingle数为144794，结果如下图所示：

 

2.把shingle哈希到不同的桶中

桶编号的长度选择比总shingle稍大的145678，针对每个文档中的每个Shingle形成<k,v>对，其中k为文件名，v为shingle的hash值，结果如下图所示：

5.3 MinHashing

对于来自于相同文件的<k,v>,用100个Hash函数进行处理，输出多个<k,v*>，其中k为文件名，v*为minhash，然后再需要将这些相同文件的<k,v*>合并成<k,v**>，结果如下图所示：

 

5.3 LSH

根据上一步MinHashing的输出，选择b为20,r为5，输入<k,[v1,….v100]>, 其中k为文件名，[v1,….v100]为100个minhash值，因为有912个文件，所以桶编号可以设置为比文件总数稍大的999，输出<h*, k>，h*为桶编号，k为落入该桶的所有文件名，结果如下图所示：

对于每个桶h*, 比较落入该桶的文档即可知道这些文档的相似情况。