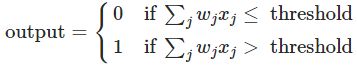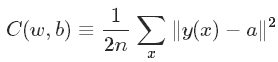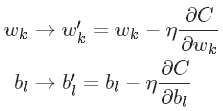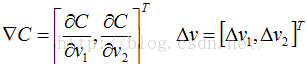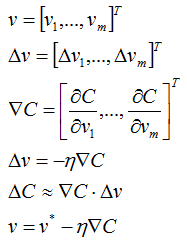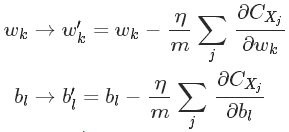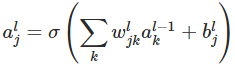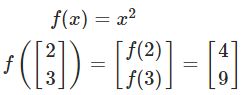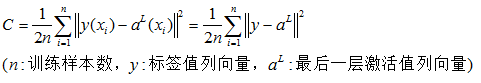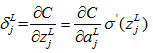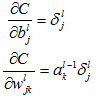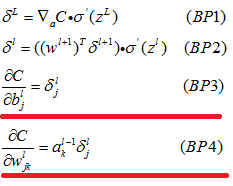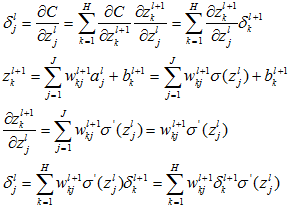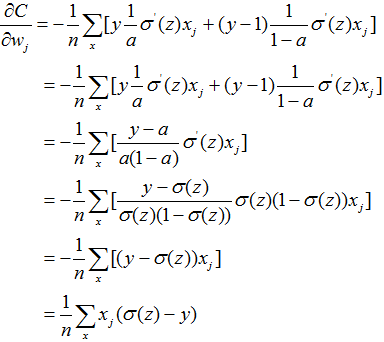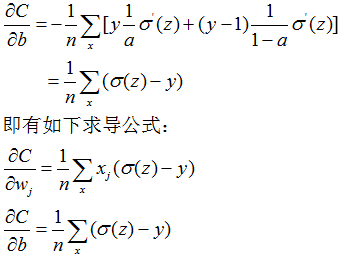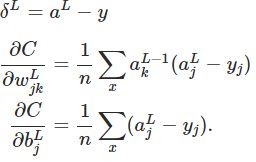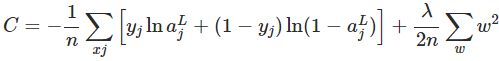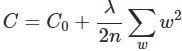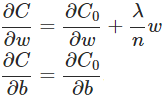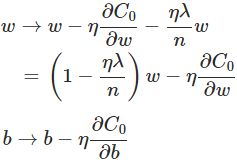神经网络和深度学习-学习总结

1. 简介

    神经网络和深度学习是由Michael Nielsen所写，其特色是：兼顾理论和实战，是一本供初学者深入理解Deep Learning的好书。

2. 感知器与sigmoid神经元

2.1 感知器(Perceptrons)

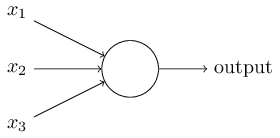
     感知器工作原理：接收一系列二进制输入，经过特定的规则计算之后，输出一个简单的二进制。

     

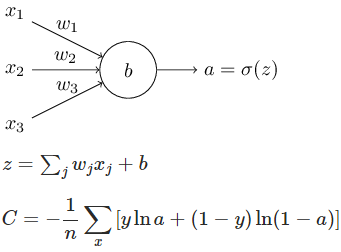
     计算规则：通过引入权重(weights)表示每个输入对于输出的重要性，则有

    

    记 w⋅x=∑jwjxj ，b=-threshold，则有

    

    其w是权重，b是偏差。

2.2 Sigmoid神经元(Sigmoid Neurons)

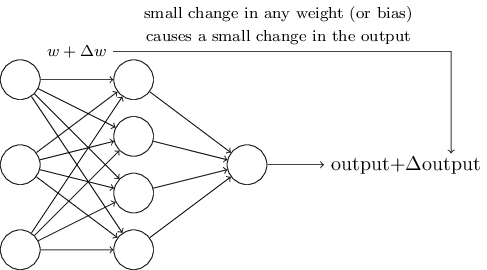
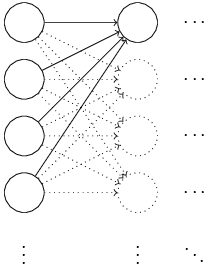
    为了使学习变得可能，需要具备的【学习特征】：权重或偏差有较小的变化，导致输出也有较小的变化。如下图所示：

        

      感知器网络存在的缺陷是：某个感知器较小的权重或偏差变化，可能导致输出在0与1之间进行翻转。所以包含感知器的网络不具备【学习特征】。

   幸运的是：Sigmoid神经元具有此【学习特征】，即其较小的权重或偏差变化，导致其输出变化较小。

   Sigmoid函数：

       

   Sigmoid神经元输出：

        

    感知器与sigmoid神经元的差别：

     1） 感知器只输出0或1

     2）sigmoid神经元不只输出0或1，而可输出[0,1]之间的任意值

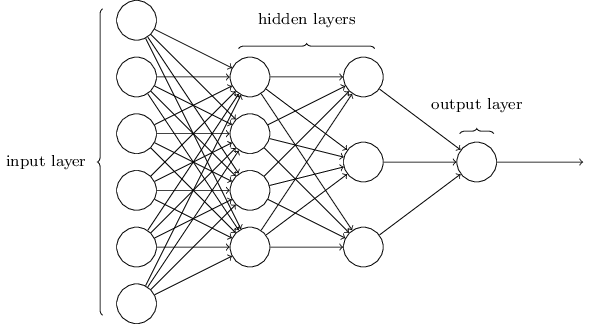
3. 神经网络架构

    

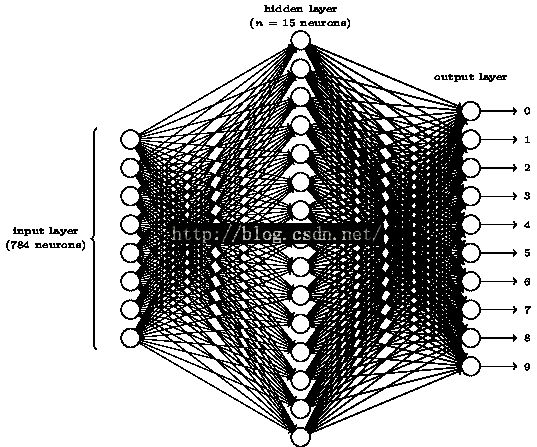
3.1 手写数字识别

    

    训练图像大小为28x28，每个训练图像有一个手写数字。

    在输出层，如果第一个神经元被激活(即其输出接近1)，则此网络认为此手写数字为0；

           如果第二个神经元被激活(即其输出接近1)，则此网络认为此手写数字为1；

           其它以此类推。

3.2 算法描述

    设x表示训练图像，则x是一个28x28=784维列向量。

    表示输入图片x是数字6   。

    需要寻找一个算法来发现w和b，使其输出接近标签值，为了量化接近程序，定义如下成本函数：

    

    w：所有权重的集合

    b：所有偏差的集合

    n：训练样本数

    a： 输出向量(其值依赖x,w,b)

    x：一幅训练图像

    ||v||：表示向量的范数，即向量的长度

    C：二次成本函数(mean squared error or MSE)

    如果接近于0，表示y(x)接近输出a，即学习效果很好。

    此成本函数中，w和b为变量。

    注：hidden layers和output layer中的每个神经元对应一个组w、b。

3.2.1 学习目标

    如何找到满足要求的w和b：答案是梯度下降法(Gradient Descent)

    1）最小化二次成本函数

    2）检测分类的准确性

    学习目标：在训练神经网络中，找到使二次成本最小的w和b的集合。

3.2.2 梯度下降更新规则

   

    ：表示学习速度（Learning Rate)

     此规则用于在神经网络中学习参数w和b。

3.2.3 算法推导（梯度下降法： gradient descent）

    要求极小值，先讨论具有2个变量的简单情况，然后再推广：

    

    令，为梯度向量，则有：

    

     现在的问题是如何选择，使负数，则有：

     

      则v的更新规则为：

      

      按此规则，一步一步跌代，C值不断减少，直到全局最小值。

      总之，梯度下降法是：重复计算梯度，然后向相反的方向移动（即下坡最快最陡的方向），如下图所示：

      

      上面讨论了只有两个变量的情况，现在推广到m个变量的情况，对应公式如下：

      

3.2.4 随机梯度下降法(Stochastic Gradient Descent)

       为不减少计算量，把n个学习样本分成很多组，每组有m个学习样本，每次只计算一个组，则有如下推导：

      

        则w和b的更新规则为：

        

        注：如果m=1，则为在线学习(online)。

3.2.5 w和b的数量

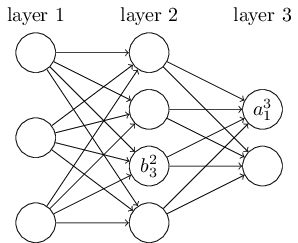
     对于hidden layers和输出层的神经元，每个神经元对应一个w向量和一个b，w向量的维数是其输入神经元的数量。第一层神经元没有w和b，其值直接输出。

     第一层就表示原始图像数据，这些数据不经任何处理，直接作为Xj参与第二层的运算，第二层首先基于每个Xj，计算其z(z=wx+b)，然后计算出sigmoid(z)，以此类推。直到最后一层，利用BP算法，先计算最后一层w和b的梯度，然后以此向前，直到计算出第二层的梯度为止。

4. BP算法(反向传播算法)

     BP(Backpropagation Algorithm) ：是一个计算成本函数梯度的算法。

     需要基于每个训练样本计算每一层的w和b的梯度，从而更新每一层的w和b。 

      BP的真正目标：是计算每个样本的偏导数：和。

4.1 定义标记符号

             

      

       则有激活值的如下公式：

       

       函数向量化有如下形式：

      

      即函数对向量的每个元素分别计算，然后生成对应的向量。

      则上面的函数向量表示为：

      

      记，则有

4.2 公式推导过程

4.2.1 计算激活值

     

4.2.2 最后一层(L层)的二次成本函数

    

4.2.3 单个训练样本(x)的二次成本函数

    

4.2.4 定义误差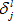

    

4.2.5 定义输出层误差

    

4.2.6 求最后一层(L层)激活值的偏导数

      

4.2.7 根据最后一层的误差计算前一层的误差

     

4.2.8 计算目标值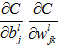

     

4.2.9 BP的四个基本方程式

     

4.3 证明四个基本议程式

4.3.1 证明BP1

      

4.3.2 证明BP2

      

4.4 BP计算过程

      

5. SGD(随机梯度下降)计算过程

    

6. 改进神经网络学习方法

    理想地，期望我们的神经网络能从自己的错误中快速地进行学习。

    神经元通过改变权重和偏差的来进行学习的学习速度由成本函数的偏导数(和)决定，所以学习速度慢的根本原因是：偏导数太小。

6.1 交叉成本函数

    交叉成本函数定义如下：

    

    对权重w的求导结果为（n为训练样本数）：

    

     

      根据上面的求导公式，则避免了在二次成本函数中由导致的学习速度慢问题。

6.2 推广交叉成本函数

      把交叉成本函数推广到具有多个神经元的多层网络中，则交叉成本函数变为：

     

      

     

    与二次成本函数相比，唯一不同的是的计算方法，其它计算方法完全相同。

7. 过拟合和规范化

7.1 过拟合(Overfitting)    

       在神经网络中，过拟合(Overfitting)是一个主要问题。此问题在现代网络中特别突出，因为现代网络有大量的权重和偏差。为了进行有效的训练，我们需要一个检测是否过拟合的方法，以防止过度训练(Overtraining)，并且我们还需要可以减少过拟合效果的技术。

      最直接的检测过拟合的方法是：跟踪测试数据在训练过的网络中的准确性。如测试数据分类的准确性不再改善，我们应当停止训练；或测试数据分类的准确性和训练数据分类的准确性都不再改善，我们应当停止训练。

      如果对训练样本过拟合，则其推广能力就差，导致对新的数据的预测或分类的准确性变差。

7.2 规范化(Regularization)-减少过拟合

      增加训练数据是减少过拟合的方法之一。
      规范化(Regularization)也是减少过拟合的方法之一。有时候被称为权重衰减（weight decay）或者L2 规范化。L2 规范化的思想是增加一个额外的项到成本函数中，这个项叫做规范化项。规范化的交叉熵如下：

      

      >0是规范化参数(regularization parameter)

     

     C0是原来常规的成本函数。 如果较小，我们期望最小化原始成本函数；如果较大，我们期望最小化权重。

     则可得：

     

     可进一步得到：

     

    权重衰减因子：

    针对小批量训练样本(m个)，则有：

    

7.3 为什么规范化可以减少过拟合

   权重越小，复杂度就越低；可以为数据提供更简洁更有力的解释。

     当有异常输入时，小的权重意味着网络输出变化不大，即不易学习到数据中的局部噪声。总而言之，规范化网络基于训练数据的主要规律，从而创建一个相对简单的模型，并且拒绝学习训练数据中的噪声（异常数据）。这样强制网络学习数据的本质规律，并把学到的规律进行更好地推广。

8. 权重初始化

    可加快学习速度。    

    假设输入层有500个神经元，且已经使用归一化的高斯分布初始化了连接第个隐层的权重。如下图所示：

    

    为了简化，设输入层一半神经元值为1，另一半为0。让我们考虑隐层神经元输入的带权和z：

    

       其中500项消去了，因为对应的输xj 为0。所以z 是包含501个归一化的高斯随机变量的和，包含500个权重项和1个偏差项。因此z本身是一个均值为0、标准差为(方差为501)的高斯分布。它是一个非常宽的高斯分布，根本不是非常尖的形状：

     

    注：

       若随机变量X服从一个数学期望为μ、方差为σ^2的高斯分布，记为N(μ，σ^2)。

       正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。

       

       标准正态分布服从N(0,1)
       两个都服从正太分布的变量,例如X服从N(a,b)，Y服从N(c,d)，且X和Y相互独立，则有：

       1）X+Y服从N(a+c,b+d)

       2）X-Y服从N(a-c,b+d)

       即两变量相加减时，期望相应加减，方差始终是相加。

       从上图上可以看出|z|会变得很大，即z>>1或z<<-1。如果这样，隐层神经元的输出就会接近1或者0，即隐层神经元进入饱和状态了。

     

      

学习于：http://neuralnetworksanddeeplearning.com/index.html