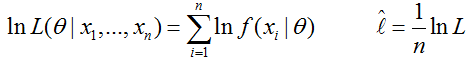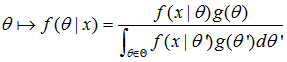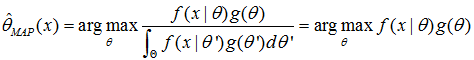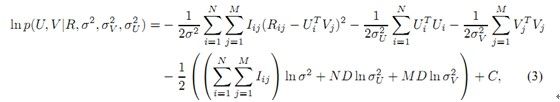基于概率的矩阵分解原理详解（PMF）

上一篇博客讲到了推荐系统中常用的矩阵分解方法， RegularizedMF 是对 BasicMF 的优化，而 PMF 是在 RegularizedMF 的基础上，引入概率模型进一步优化。假设用户 U 和项目 V 的特征矩阵均服从高斯分布，通过评分矩阵已知值得到 U 和 V 的特征矩阵，然后用特征矩阵去预测评分矩阵中的未知值。

若用户 U 的特征矩阵满足均值为0，方差为 σ 的高斯分布，则有如下等式。之所以连乘，是因为 U 的每个观察值 Ui 都是独立同分布的。
p(U|σ2U)=∏Ni=1N(Ui|0,σ2UI)

同理：项目V的特征矩阵满足如下等式：
p(V|σ2V)=∏Ni=1N(Vi|0,σ2VI)

其中 N(x|u,σ2) 表示变量 x 满足均值为u，方差为 σ2 的高斯分布。

假设真实值 R 和预测值 R∗ 之差也符合高斯分布，那么有如下概率分布表示， P(Rij−UTiVj|0,δ2) 通过平移有 P(Rij|UTiVj,δ2)， 那么：

那么评分矩阵 R 的条件概率如下：

P(R|U,V,σ2)=∏Ni=1∏Mj=1[N(Rij|UTiVj,σ2)]Iij

这里 U 和 V 是参数，其余看作超参数（即作为 U和V 的参数-参数的参数，PMF中通过人工调整超参数，后面要写的BPMF是通过MCMC方法自动选出最优超参数的）。假设 U和V 互相独立，可以通过贝叶斯公式得到 R，U，V 的联合分布：

P(U,V|R,σ2,σ2U,σ2V)=P(R|U,V,σ2)P(U|σ2U)P(V|σ2V) =∏Ni=1∏Mj=1[N(Rij|UTiVj,σ2)]Iij∏Ni=1N(Ui|0,σ2UI)∏Mj=1N(Vj|0,σ2iI)

为什么要转换为这种形式呢？这还要从极大似然估计（ MLE ）和最大后验概率（ MAP ）说起。

最大似然估计：假设观察数据满足 F 分布，但是不知道分布参数，那么 MLE 就是根据采样数据来评估出参数，而且假设所有采样（观察的样本数据）都是独立同分布。　
服从参数为 θ 的 F 分布的函数我们用 fD 来表示，然后我们从这个分布中抽出一个具有n个值的采样 X1,X2……Xn ，那么样本的概率表示为：

P(x1,x2,…,xn)=fD(x1,x2,…，xn|θ)

仔细想想，当前样本数据已知，未知参数只有 θ ，我们就要想 θ 为多少才会产生这样的样本呢？我们就要找一个合适的 θ 使得当前的样本数据满足该分布。极大似然估计的目标是在所有可能的θ取值中，寻找一个值使这个采样的“可能性”最大化。通常采用通过求极值的方式求得关于 θ 一元函数的最优值的方式。

求极大似然估计(MLE)的一般步骤是：

1. 由总体分布导出样本的联合概率函数 (或联合密度);

2. 把样本联合概率函数(或联合密度)中自变量看成已知常数,而把参数 看作自变量,得到似然函数L( θ );

3. 求似然函数L( θ ) 的最大值点(常常转化为求ln L( θ )的最大值点) ，即 θ 的MLE;
4. 在最大值点的表达式中, 用样本值代入就得参数的极大似然估计值 .

似然函数：

通常取对数（对数似然），以便将乘化为加：

这样，待估计参数就可以表示为如下形式：

同理若待估计参数有两个，比如样本服从高斯分布，如下式，可以通过求偏导数得到估计值。

这样，PMF为何要转换为 R，U，V 的联合分布，且 U和V 在前面就解释通了， U和V 作为待求参数，要利用 R 里的已知值计算出来（评估），然后为何会转为等式右边，这得需要最大后验概率的知识。

最大后验概率：

最大后验估计，融入了要估计量的先验分布在其中，也就是说待估计量θ本身也满足某概率分布g(θ)（已知）, 称为先验分布。这样根据贝叶斯理论，似然函数有如下表示：（这里f(θ|x)等价l(θ|x)是似然函数，表示已知样本数据x集合，来评估θ的值（条件概率），但后面的等式就只关乎密度函数f了）。

贝叶斯公式大家都懂，这里我就说说分母为啥写成这个形式。此f是关于和θ和x的联合分布密度，不是我么理解的事件ABC，同时发生等。正常来说分母应该是f(x),表示只考虑x这一影响因素，要消除θ的影响，那么我么是通过对θ积分来消除θ，分母的结果最终是等于f（x）的，分子是等于f(θ,x)的。最终，待估参数表达为：

分母的积分结果得到关于f(x)的密度函数，已知的对不。这样，最大后验概率的待估参数就是在最大似然估计的结果后面多乘了个待估参数的先验分布。写到这，大家就该懂了为啥等式右边是那种形式了，在最大似然估计的基础上要添加 U和V 本身的先验分布。

将 R，U，V 的联合密度对数化:

最大化后验概率U和V（最大可能性），等价于求下式的最小值：

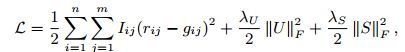
其中：

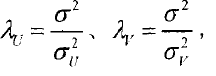
解传统矩阵分解可以采用各种优化方法，对于概率分解，由于最后求的是参数U和V的最大似然估计，因此可以用最大期望法（EM）和马尔可夫链蒙特卡罗算法（MCMC）。这里就不多说了。

PMF也有改进的地方，它没有考虑到评分过程中用户的个人信息，比如有的用户就是喜欢打低分，有的项目（电影）质量就是不高，分肯定高不了等，这样可以采用加入偏置的概率矩阵分解（贝叶斯概率矩阵分解BPMF），将在后面的博客中写出，会给出链接。

补充：联合分布f（x,y），其中x和y无必然联系，x可以理解为老师课讲得好，y理解为课开在周六，那么f表示这节课选课的人数的概率密度，联合分布的概率跟f(x)一样，也是通过积分来求，f(x)求面积，而f(x,y)是求体积。

最大似然估计和最大后验概率是参考了这两篇篇博客：

http://blog.csdn.net/upon_the_yun/article/details/8915283
http://wiki.mbalib.com/wiki/%E6%9C%80%E5%A4%A7%E4%BC%BC%E7%84%B6%E4%BC%B0%E8%AE%A1