POJ 3264 Balanced Lineup (RMQ)
Description
For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. To keep things simple, he will take a contiguous range of cows from the milking lineup to play the game. However, for all the cows to have fun they should not differ too much in height.
Farmer John has made a list of Q (1 ≤ Q ≤ 200,000) potential groups of cows and their heights (1 ≤ height ≤ 1,000,000). For each group, he wants your help to determine the difference in height between the shortest and the tallest cow in the group.
Input
Line 1: Two space-separated integers, N and Q.
Lines 2..N+1: Line i+1 contains a single integer that is the height of cow i
Lines N+2..N+Q+1: Two integers A and B (1 ≤ A ≤ B ≤ N), representing the range of cows from A to B inclusive.
Output
Lines 1..Q: Each line contains a single integer that is a response to a reply and indicates the difference in height between the tallest and shortest cow in the range.
Sample Input
6 3
1
7
3
4
2
5
1 5
4 6
2 2
Sample Output
6
3
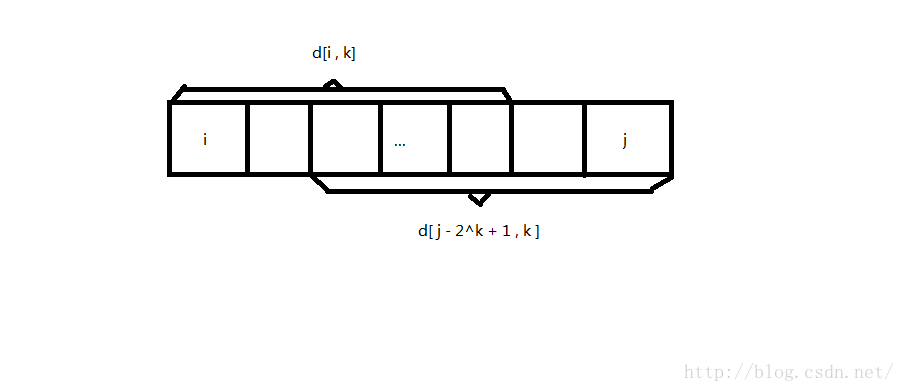
查询时,令 k 为满足 2^k <= R - L + 1 的最大整数,则以 L 开头,以 R 结尾的两个长度为2^k 的区间合起来即覆盖了查询区间[L , R]。由于是取最值,有些元素重复了也没关系。
For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. To keep things simple, he will take a contiguous range of cows from the milking lineup to play the game. However, for all the cows to have fun they should not differ too much in height.
Farmer John has made a list of Q (1 ≤ Q ≤ 200,000) potential groups of cows and their heights (1 ≤ height ≤ 1,000,000). For each group, he wants your help to determine the difference in height between the shortest and the tallest cow in the group.
Input
Line 1: Two space-separated integers, N and Q.
Lines 2..N+1: Line i+1 contains a single integer that is the height of cow i
Lines N+2..N+Q+1: Two integers A and B (1 ≤ A ≤ B ≤ N), representing the range of cows from A to B inclusive.
Output
Lines 1..Q: Each line contains a single integer that is a response to a reply and indicates the difference in height between the tallest and shortest cow in the range.
Sample Input
6 3
1
7
3
4
2
5
1 5
4 6
2 2
Sample Output
6
3
0
这道题裸考范围最值问题,题意给定一些数,给一个区间求这个区间最大值与最小值的差。
RMQ详解:
范围最小值问题(Range Minimum Query,RMQ)。给一个 n 个元素的数组A1,A2,...,An,查询范围(L,R)中的最小值和最大值。
Sparse-Table算法,它预处理时间O(nlogn),但查询只需O(1)。
令 d(i, j) 表示从 i 开始,长度为 2^j 的一段元素中的最小值,则状态转移:d( i , j ) = min{ d( i , j - 1 ), d(i + 2^( j - 1) , j - 1 )},原理如下图:
注意2^j <= n,因此 d 数组的元素个数不超过 nlogn ,而每一项都可以在常数时间计算完毕,故总时间为O(nlogn)。
预处理代码:
void RMQ_init(const vector<int>& A)
{
int n = A.size();
for (int i = 0; i < n; i++)
d[i][0] = A[i]; //初始化
for (int j = 1; (1 << j) <= n; j++)
for (int i = 0; i + (1 << j) - 1 <n; i++) ///i从0开始保证了区间的无缝覆盖
d[i][j] = min(d[i][j - 1], d[i + (1 << (j - 1))][j - 1]);
}
查询时,令 k 为满足 2^k <= R - L + 1 的最大整数,则以 L 开头,以 R 结尾的两个长度为2^k 的区间合起来即覆盖了查询区间[L , R]。由于是取最值,有些元素重复了也没关系。
查询代码:
int RMQ(int L, int R)
{
int k = 0;
while ((1 << (k + 1)) <= R - L + 1) k++; <span style="font-family: Arial, Helvetica, sans-serif;">///如果2^(k+1)<=R-L+1,那么看还可以加1</span>
return min(d[L][k], d[R - (1 << k) + 1][k]);
}
本题代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#define N 50000+10
using namespace std;
int dmax[N][16],dmin[N][16];///2^16>N
vector<int>Q;
void RMQ_init(const vector<int>& A)
{
int n = A.size();
for (int i = 0; i < n; i++)
dmax[i][0]=dmin[i][0]= A[i]; //初始化
for (int j = 1; (1 << j) <= n; j++)
for (int i = 0; i + (1 << j) - 1 <n; i++) ///i从0开始保证了区间的无缝覆盖
{
dmax[i][j] = max(dmax[i][j - 1], dmax[i + (1 << (j - 1))][j - 1]);
dmin[i][j] = min(dmin[i][j - 1], dmin[i + (1 << (j - 1))][j - 1]);
}
}
int RMQ_max(int L, int R)
{
int k = 0;
while ((1 << (k + 1)) <= R - L + 1) k++;///如果2^(k+1)<=R-L+1,那么看还可以加1
return max(dmax[L][k], dmax[R - (1 << k) + 1][k]);
}
int RMQ_min(int L, int R)
{
int k = 0;
while ((1 << (k + 1)) <= R - L + 1) k++;
return min(dmin[L][k], dmin[R - (1 << k) + 1][k]);
}
int main()
{
int n,m,i,a,L,R;
while(~scanf("%d%d",&n,&m))
{
for(i=0; i<n; i++)
{
scanf("%d",&a);
Q.push_back(a);
}
RMQ_init(Q);
while(m--)
{
scanf("%d%d",&L,&R);
printf("%d\n",RMQ_max(L-1,R-1)-RMQ_min(L-1,R-1));///预处理是从0开始的,所以区间边界都减一
}
}
}