ML—EM

华电北风吹
日期：2016-05-07

EM算法是与kmeans极其相似的一个迭代优化算法，主要用于带隐含变量的极大似然估计问题。EM与kmeans一样，能够保证收敛，但不能保证全局收敛，对初始值敏感。

0 . Jensen不等式
在 n 维线性空间里面，如果有 f′′(X)≥0 (即 f(X) 是下凸函数)，则有 E[f(X)]≥f(E[X]) 。

条件更严格一点，要求 f(X) 是严格的下凸函数 (f′′(x)>0) 时， E[f(X)]=f(E[X]) 的充要条件为随机变量 X 是一个单点分布( X 取某个值的概率为1)。
上凸函数结论有此类似的性质。

一、EM算法迭代过程图示
假设有m个相互独立的训练样本 {x(1),x(2),...,x(m)} 服从于一个分布类型已知，但参数未知的分布，并且随机变量 x 的观测值受隐含变量 z 影响,引入概率密度函数 Qi(z) ，来描述隐含变量 z 的分布( ∑zQi(z)=1,Qi(z)≥0 )。如果希望对模型参数进行极大似然估计，就可以利用EM算法，迭代求解。
l(θ)=∑mi=1logp(x(i);θ)=∑mi=1log∑z(i)p(x(i),z(i);θ)(1-1)
直接对1-1式进行极大似然估计问题是很困难的，EM算法利用迭代的思想进行求解。EM算法主要分两步迭代：第一步(E-step)，利用现有的模型参数 θ ，更新每个样本的隐含变量分布 Qi(z) ；第二步(M-step)，利用上一步的每个样本的隐含变量分布 Qi(z) ，进行总体样本的极大似然估计，更新模型参数 θ 。

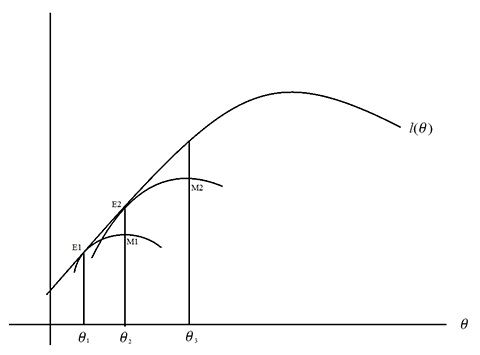
对于初始参数 θ1 ，经过第一次E-step以后，可以找到 l(θ) 的第一个下界(E1处)，然后进行第一个M-step，对 θ 更新，找到 θ2 ，然后继续进行第二个E-step到达E2，…。直到迭代过程收敛。

二、EM算法理论推导
EM算法流程为:
———————————————————————————————–
Algorithm1:
Repeat until convergence
　　　(E-step) For each i, set
　　　　　　 Q(t)i(z(i))=p(z(i)|x(i);θ(t))
　　　(M-step) Set
　　　　　　 θ(t+1):=argmaxθ∑i∑z(i)Q(t)i(z(i))logp(x(i),z(i);θ)Q(t)i(z(i))
———————————————————————————————–
理论推导过程如下：
1) E-step：
看下式，
l(θ)=∑mi=1logp(x(i);θ)

　 　 =∑mi=1log∑z(i)p(x(i),z(i);θ)
　 　
　 　 =∑mi=1log∑z(i)Qi(z(i))p(x(i),z(i);θ)Qi(z(i))

　 　 ≥∑mi=1∑z(i)Qi(z(i))logp(x(i),z(i);θ)Qi(z(i))
(2-1)
公式2-1最后一步的推导用到了前面讲的Jensen不等式(这里 log 函数是严格上凸函数，应用上凸函数的jensen不等式 f(E[X])≥E[f[X]] )。根据Jensen不等式取等号的条件，当满足
p(x(i),z(i);θ)Qi(z(i))=c(2-2)
其中c为常数，便可以得到似然函数在当前参数 θ 下， l(θ) 的下界。在这时 E[f[X]] 达到最大，因此，E-step也被称为期望最大化步。
接下来，根据式2-2，可以知道
Qi(z(i))∝p(x(i),z(i);θ)(2-3)
又因为 ∑zQi(z(i))=1 可以更进一步的有，

Qi(z(i))=p(x(i),z(i);θ)∑zp(x(i),z;θ)

　　　 　 =p(x(i),z(i);θ)p(x(i);θ)
　　　 　
　　　 　 =p(z(i)|x(i);θ)
(2-4)
这里也就是说，在当前参数为 θ 的条件下，要想得到 l(θ) 的下界，只需要使得每个样本的隐含变量 z(i) 的分布是关于 x(i) 的后验分布即可。
2) M-step
在接下来的M-step，只需要根据这一迭代过程中对 x(i) 的隐含变量 z(i) 确定的后验分布 Qi(z(i)) ，利用普通的极大似然估计法即可得到 Qi(z(i)) 给定时，使的 l(θ) 取极大值的 θ^ 。

三、EM算法的收敛性分析
从以上讨论已经看到 l(θ) 受 θ 和 Qi(z) 双重影响。为了叙述方便定义
J(Q,θ)=∑mi=1∑z(i)Qi(z(i))logp(x(i),z(i);θ)Qi(z(i))(3-1)
对于EM算法的迭代过程是否会收敛，只需要看看相邻两次的似然函数值有没有增大即可。因此只需要证明 l(θt)≤l(θt+1) 。由1-1可得 l(θ)=∑mi=1log∑z(i)Qi(z(i))p(x(i),z(i);θ)Qi(z(i)) 。
所以
l(θ(t))=∑mi=1log∑z(i)Qi(z(i))p(x(i),z(i);θ(t))Qi(z(i))(3-2)
所以有，
l(θ(t+1))=∑mi=1log∑z(i)Qi(z(i))p(x(i),z(i);θ(t+1))Qi(z(i))
　　　　　 ≥∑mi=1∑z(i)Qi(z(i))logp(x(i),z(i);θ(t+1))Qi(z(i))
四、混合高斯模型
利用EM算法求解混合高斯模型的极大似然估计是EM算法的一个简单且经典的应用。
求解过程主要包含两步迭代。

五、EM算法其它应用
利用EM迭代求解极大似然估计问题的还有很多，例如混合贝叶斯模型，因子分析，隐马尔科夫模型等。最近也看到一篇将EM应用与社交网络拓扑结构分析的论文。