HDU 1030.Delta-wave【找规律、最短路】【3月15】

Delta-wave

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 7451    Accepted Submission(s): 2873

Problem Description

A triangle field is numbered with successive integers in the way shown on the picture below. 



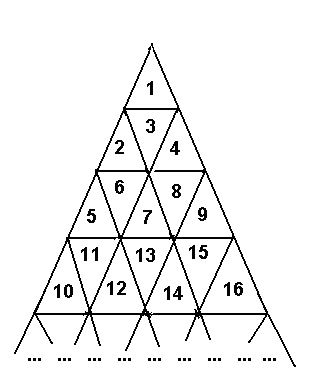
The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route. 

Write the program to determine the length of the shortest route connecting cells with numbers N and M. 

 

Input

Input contains two integer numbers M and N in the range from 1 to 1000000000 separated with space(s).

 

Output

Output should contain the length of the shortest route.

 

Sample Input

   
   
   
   

    
    
    
    6 12 
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    3
   
   
   
   

 

按照如图所示的三角形排列，给你两个三角形的编号，问这两个三角形的最短路。

1）首先，要计算出两个三角形所在的行以及所在行的第几个位置，如果在同一行，直接用两个位置相减便是答案。

2）如果不在同一行，设n(较小的数)在第num1行的第pos1个位置，m在第num2行的第pos2个位置，两个三角形相差hang行。然后计算n所在三角形经过2*hang步能够到达num2行（m所在行）的最远位置，即向左到达num2行pos1位置，向右到达num2行pos1+2*hang位置。

3）判断pos2是否在上述范围内，如果不在，则需要2*hang+偏移量；如果在，则需判断两个三角形是否同正或同倒，同正或同倒则只需2*hang步。否则，若n为正三角形，则需2*hang-1步，若m为正三角形，则需2*hang+1步

代码如下：

#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
    int f[35000][2];
    for(int i = 0; i < 35000; ++i) //记录第i行三角形的起始数字
    {
        f[i][0] = i*i  - 2*i + 2;//起
        f[i][1] = i*i;//终
    }
    int n, m, num1, num2;
    while(scanf("%d %d", &n, &m) != EOF)
    {
        int a = n, b = m;
        n = min(a, b);
        m = max(a, b);
        for(int i = 0; i < 35000; ++i)
        {
            if(f[i][0] <= n && f[i][1] >= n) num1 = i;
            if(f[i][0] <= m && f[i][1] >= m) num2 = i;
        }
        int pos1 = n - f[num1][0] + 1;//计算n在第num1行的第几个位置
        int pos2 = m - f[num2][0] + 1;//计算m在第num2行的第几个位置
        int hang = num2 - num1;//计算n和m相差的行数
        int maxpos = pos1 + 2*hang;//计算n向下2*hang步最右在m所在行的哪个位置
        if(pos2 <= maxpos && pos2 >= pos1)//m所在位置在n向下2*hang步能到的范围内
        {
            int s1, s2;//记录两个三角形的方向
            if(pos1%2 == 1) s1 = 1;//第奇数个三角形是正着的
            else s1 =  -1;
            if(pos2%2 == 1) s2 = 1;//同上
            else s2 = -1;
            if(s1 == s2) cout << 2*hang << endl;//同正或者同倒
            else if(s1 == 1) cout << 2*hang - 1 << endl;//n是正三角，m是倒三角
            else cout << 2*hang + 1 << endl;//n是倒三角，m是正三角
        }
        else//n向下2*hang步到不了m
        {
            if(pos2 < pos1) cout << 2*hang + pos1 - pos2 << endl;//m的位置在n向下2*hang步能到达最远位置的左边
            else cout << 2*hang + pos2 - maxpos << endl;//右边
        }
    }
    return 0;
}