欧拉回路问题(算法导论22.2-8 和22-3)
22.3 欧拉回路的算法来自1873年的Hierholzer,前提是假设图G存在欧拉回路,即有向图任意点的出度和入度相同。从任意一个起始点v开始遍历,直到再次到达点v,即寻找一个环,这会保证一定可以到达点v,因为遍历到任意一个点u,由于其出度和入度相同,故u一定存在一条出边,所以一定可以到达v。将此环定义为C,如果环C中存在某个点x,其有出边不在环中,则继续以此点x开始遍历寻找环C’,将环C、C’连接起来也是一个大环,如此往复,直到图G中所有的边均已经添加到环中。
数据结构如下:
(1) 使用循环链表CList存储当前已经发现的环;
(2) 使用一个链表L保存当前环中还有出边的点;
(3) 使用邻接表存储图G
使用如下的步骤可以确保算法的复杂度为O(E):
(1) 将图G中所有点入L,取L的第一个结点
(2) 直接取其邻接表的第一条边,如此循环往复直到再次到达点v构成环C,此过程中将L中无出边的点删除。环C与环CList合并,只要将CList中的点v使用环C代替即可。
(3) 如果链表L为空表示欧拉回路过程结束,否则取L的第一个结点,继续步骤(2)
22.2-8要求将无向图的每条边恰好按照两个方向各走一次,实际上可以将此无向图看作一个有向图,无向图中的任意一条边(u,v),都扩充成为有向图中的两条边(u,v)和(v,u),根据一笔画的欧拉定理,因为此有向图任意点的出度和入度相同,故此有向图存在欧拉回路,而且可以从任意点开始。
此问题在BFS(宽度优先搜索)章节,刚开始无论如何也无法和BFS联系起来,直到看到22.3中欧拉回路的算法才逐渐明白。算法思路如下:
(1) 与传统的欧拉回路算法类似,只不过此处的环很简单,直接是BFS中的边,注意确保每条边访问一次且仅访问一次;
(2) 当访问结点u时,将环路径中的点u替换为一个小环路径,即所有与u相邻的边且没有被访问过的边,具体来说包括所有的tree edge,同时还有第一次访问的cross edge
举例如下:
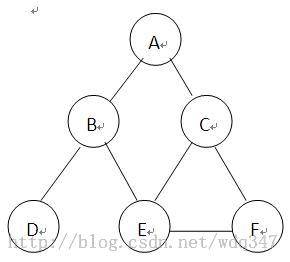
(1) 第一轮BFS,队列中仅在结点A,环路径为A
(2) 第二轮BFS,访问到边A=>B时,环路径为A=>B=>A,再访问到A=>C时,环路径为A=>B=>A=>C=>A,队列中有点B、C,环路径为A=>B=>A=>C=>A
(3) 第三轮BFS,队列中有D、E、F,环路径为A=>(B=>D=>B=>E=>B)=>A=>(C=>E=>C=>F=>C)=>A
(4) 第四轮BFS,队列中为空,最终的环路径为
A=>(B=>D=>B=>(E=>F=>E)=>B)=>A=>(C=>E=>C=>F=>C)=>A