周末来一发之五一周赛
题目链接:http://acm.nefu.edu.cn/JudgeOnline/contestShow.php 传送门:nefu
1. Rotate Circle
题面描述:
Rotate Circle
Problem:A
Time Limit:1000ms
Memory Limit:65535K
Description
I know you are very smart and good at math. But how about the analytic geometry. For example, if I give you a compass and you can easily draw a circle of radius R at point P(x, y). However, I can only give you a circle of radius R at point O(x1, y1) now. How to get a circle whose center at P-point and radius is R. We can ensure that P-point and O-point do not overlap. You can only use one kind of operation to make the circle rotate any angle around any point which at the border of the circle. So you can make the circle rotate to P-point by using the circle at O-point after some operation. What is the minimum number of operation to do this .( operation of rotating around point at border )
Input
There are several test cases. Each test case contains 5 positive integers R , x , y , x1 , y1 as the description in one line. ( R ≤ 1000 , 0 ≤ x ,y ≤100,000,000 and 0 ≤ x1 , y1 ≤ 100,000,000 ). The input will finish with the end of file.
Output
For each the case, your program will output one positive integers indicate the answer.
Sample Input
5 47 72 97 8 4 44 38 32 79
Sample Output
9 6
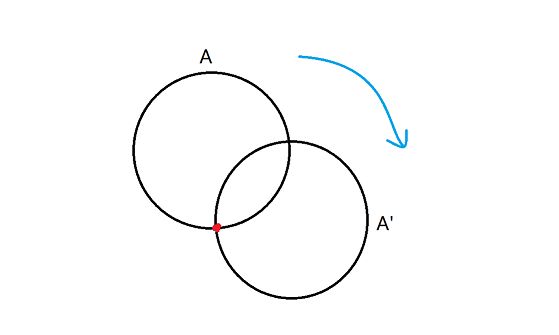
如果说我们有圆规的话,我们很容易就能画出一个已知半径和圆心的圆,但是我们现在只有一个已知其圆心O和半径R的圆所以我们通过绕圆边界上任意一点旋转任意角度的方法,得到一个圆心在点P且半径为R的圆,求最少需要进行旋转的次数。
题目分析:
为了使旋转的次数最少,我们需要沿着OP连线的方向以最大长度进行旋转,即最大长度就是圆的直径,对于最后一次旋转就要比较用心一点,绕着一个点旋转一个合适的角度,恰好可以使圆心落在P点即可。所以需要进行移动的次数就等于|OP|/R向下取整在加1.
代码实现:
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int main()
{
long long x,y,x1,y1;
int r;
long long num=0;
while(scanf("%d%lld%lld%lld%lld",&r,&x,&y,&x1,&y1)!=EOF)
{
long long d=(long long)sqrt((x1-x)*(x1-x)+(y1-y)*(y1-y));
num=(long long)d/(2*r);
printf("%lld\n",num+1);
}
return 0;
}
2. Cut The Cake:
题面:
Cut The Cake
Problem:F
Time Limit:1000ms
Memory Limit:65535K
Description
Today is Julia's birthday, she was so delightful that she decided to buy a big cake and celebrate with her friends. The cake is circular in shape. Now a total of n people will eat the cake, so Julia cut the cake equally into n shares. But m persons say they want to eat the cake too. So now there are n + m people want to eat the cake. Please answer, how many times at least can Julia cut n pieces of cakes equally into n+m pieces? (Julia can only cut from the center of the circle to circumference, put several pieces of cakes together can be seen as one piece)
Input
a number t will be input on the first line, then t lines will be follow. Each line will contain two integers n and m. 1<=t <=10000, 1<=n,m<=1000
Output
For each case, output the minimum times of cut in one line.
Sample Input
2 2 1 3 1
Sample Output
2 3
蛋糕需要平均分,一开始有n个人,后来又来了m个人,问从n个人到n+m个人还需要再切几刀蛋糕。
题目分析:
我们规定,从蛋糕圆心到蛋糕边缘的半径为一刀,且一个人的时候我们也把蛋糕切了一刀,且这一刀并没有把蛋糕分开。找规律,通过需要均分的度数来确定需要的刀数,比如,原来有6个人(60度一块),又来了9个人(40度一块),可以重复的刀数为120度,240度,360度(0度),所以需要切的刀数为6+9-gcd(6,9)。所以,此题所需刀数为m+n-gcd(m,n)。
代码实现:
#include <iostream>
using namespace std;
int gcd(int a,int b)
{
if(!b)
return a;
else
return gcd(b,a%b);
}
int main()
{
int t;
int n,m;
cin>>t;
while(t--)
{
cin>>n>>m;
m=m+n;
if(m%n==0)
cout<<m-n<<endl;
else
{
if (gcd(m,n)==1)
cout<<m-1<<endl;
else
cout<<m-gcd(m,n)<<endl;
}
}
return 0;
}
3.Lazy People:
题面:
Lazy People
Problem:I
Time Limit:1000ms
Memory Limit:65535K
Description
On a flat map, there are n straight lines ,which divide the map into many regions, two regionsare adjacent if and only if they have a common boundary edges. Walk from one region to its adjacent region cost exactly only one unit of energy.You can’t walk from one to another if this two regions is not adjacent. SmallSmallBule's home is on Point P. Every day,he needs to go to school which is located at Point Q, P and Q are located in different regions. Since SmallSmallBlue is very lazy,he wants to know what is the minimum units of energy to be cost to go to school from home. Now,he needs your help to calculate the answer.
Input
the first line has a number T,(T<=22),which is the number of testcases. for each testcase,the first line has two integers xs,ys(-10^6<=xs,ys<=10^6),,which is the location of SmallSmall blue's home. the second line has two integers xh,yh(-10^6<=xh,yh<=10^6),which is the location of school. the third line has a number n(n<=400),which is the number of straight lines. then the next n lines,each line has three integers,ai,bi,ci,(-10^6<=ai,bi,ci<=10^6) which are to represent the straight line ai*x+bi*y+c=0.
Output
for each testcase,you need to output one line which contains only one integer, which is the minimum units of energy to be cost to go from home to school.
Sample Input
2 2 2 -2 -2 2 0 2 0 2 0 0 3 3 -3 -3 3 0 2 0 1 0 1 1 0 -1
Sample Output
2 3
Hint
In the first test case,two lines is x=0 and y=0, home is (2,2), school is (-2,-2), so he needs to use up 2 units of energy.(he uses up first unit of energy by arriving at the first region which (-1,1) or (1,-1) belongs to, and uses up second unit of energy by arriving at the second region which the school belongs to)
题目大意:
已知家的坐标和学校的坐标,还有n条直线,可以把整个二维直角坐标系划分成多个部分,每跨一次区域都会消耗一格能量,求最少消耗的能量数。
题目分析:
判断家和学校这条线段和n条直线的交点个数即可,判断方法即为把两个点的坐标带入直线方程中去,如果两个值相乘==0,则说明存在一个在直线上的点,若结果<0,则说明两点在直线两侧,若结果>0,则说明两点在直线同侧。
特别注意:此题注意数据范围,由于方程系数和坐标点的范围都是10^6以内,但是把点带入坐标以后得到的就是一个long long类型才能存的下的数了,所以我们必须在long long范围内进行数据计算,否则会WA的。
代码实现:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
long long a[420],b[420],c[420];
int main()
{
long long T;
long long xs,ys,xh,yh;
long long n;
scanf("%lld",&T);
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
while(T--)
{
scanf("%lld%lld%lld%lld",&xs,&ys,&xh,&yh);
scanf("%lld",&n);
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
for(int i=0;i<n;i++)
{
scanf("%lld%lld%lld",&a[i],&b[i],&c[i]);
}
int num=0;
for(int i=0;i<n;i++)
{
if(((a[i]*xs+b[i]*ys+c[i])*(a[i]*xh+b[i]*yh+c[i]))<0)
{
num++;
}
}
printf("%d\n",num);
}
return 0;
}
4. Max a&b:
Max a&b
Problem:B
Time Limit:3000ms
Memory Limit:65536K
Description
Now give you n positive integers. You can select two integers from n integers, and calucate the (a&b). ‘&’ is a binary operator.For example, 5&6=4. Now I need you calculate the maximum value of (a&b).
Input
There are multiple test cases. For each test case.The first line contains one integer n(n<=300000), which indicates the number of integers. The following n lines. The ith line contains one positive integer ai.(ai<=10^9)
Output
For each test case, your program will output the maximum value of a&b.
Sample Input
3 2 8 10
Sample Output
8
给出n个数,求任意两个数相与的最大值。
题目分析:
按从高位到地位的贪心来处理即可,此题数据比较水,这个代码不是很强壮,如:若两个最大数的&为0的话,代码没有输出,但是能过,不幸中的万幸了。当然还有待改进,具体思路就是,先排序,然后再从最大的开始处理,把每个数的二进制位数记录下来,(由于数据为10^9即为2^30次方左右,所以不会超时)如果最大的两个数二进制位数相同,则经过&操作后,必然有所得结果最大;如果两个最大数的位数不相等,那么经过&操作之后所得结果的位数就不一定是多少位了,所以要和倒数第二个和倒数第三个这两个数的&之后的结果进行比较,不但要比较位数,还要比较结果,这样以此类推下去。
代码实现:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
long long a[300010];
int bit[300010];
int main()
{
int n;
long long maxx,t;
int b;
long long x;
int xb;
while(scanf("%d",&n)!=EOF)
{
memset(a,0,sizeof(a));
memset(bit,0,sizeof(bit));
for(int i=0; i<n; i++)
{
scanf("%lld",&a[i]);
}
//cout<<"dsyhfg"<<endl;
sort(a,a+n);
for(int i=0;i<n;i++)
{
t=a[i];
while(t>0)
{
t/=2;
bit[i]++;
}
}
for(int i=n-1; i>=0; i--)
{
if(bit[i]==bit[i-1])
{
printf("%lld\n",a[i]&a[i-1]);
break;
}
else
{
maxx=a[i]&a[i-1];
b=0;
t=maxx;
while(t>0)
{
t/=2;
b++;
}
x=a[i-1]&a[i-2];
t=x;
xb=0;
while(t>0)
{
t/=2;
xb++;
}
if(b>xb)
{
//cout<<"111hdgfj"<<endl;
printf("%lld\n",maxx);
break;
}
else if(b==bit[n-2])
{
//cout<<"222hdgfj"<<endl;
if(x>maxx)
{
maxx=x;
b=xb;
}
}
else if(b<bit[n-2])
{
//cout<<"333hdgfj"<<endl;
maxx=x;
b=xb;
}
}
}
}
return 0;
}