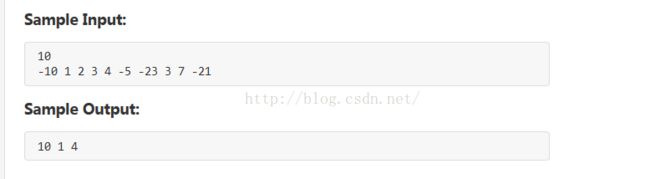
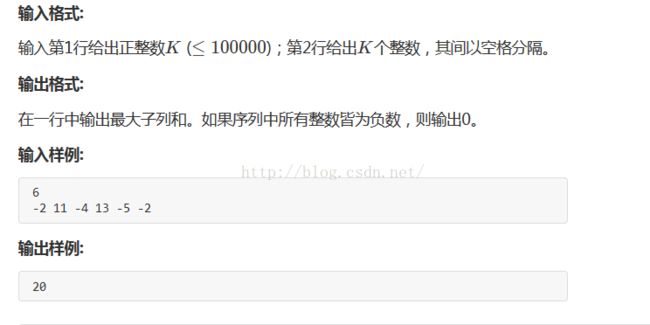
数据结构课程笔记--（1）求最大子列的问题

1.题目一

------------------------------------算法一：在线解决

#include<stdio.h>
int max(int L[],int N);
int main()
{
   int L[100000],N,i;
   scanf("%d",&N);
   for(i=0;i<N;i++)
	   scanf("%d",&L[i]);
   printf("%d\n",max(L,N));
   return 0;
}
int max(int L[],int N)
{
	int i,j,thissum,maxsum=0;
	for (i=0;i<N ;i++ )
	{
		thissum+=L[i];
		if (thissum>maxsum)
			maxsum = thissum;
		else if(thissum<0)
			thissum=0;
	}
		return maxsum;
}

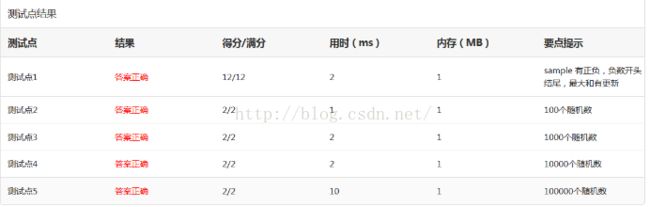
时间复杂度：T(N) = O(N)

-------------------------------算法二：两个循环

算法二：
#include<stdio.h>
int max(int L[],int N);
int main()
{
   int L[100000],N,i;
   scanf("%d",&N);
   for(i=0;i<N;i++)
	   scanf("%d",&L[i]);
   printf("%d\n",max(L,N));
   return 0;
}
int max(int L[],int N)
{
	int thissum,maxsum=0;
	int i,j;
	for (i=0;i<N ;i++ ){
		thissum = 0;
		for (j=i;j<N ; j++)
		{
			thissum += L[k];
			if(thissum > maxsum)
				maxsum = thissum;
		}
	}
		return maxsum;
}

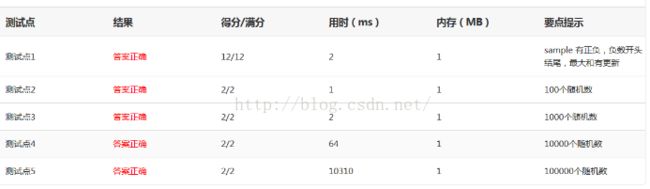
时间复杂度：T(N) = O(N^2)

2.题目2：不但求最大子列的和，还有最大子列的元素

#include<stdio.h>
int max(int L[],int N);
int main()
{
   int L[100000],N,i;
   scanf("%d",&N);
   for(i=0;i<N;i++)
	   scanf("%d",&L[i]);
   max(L,N);
   return 0;
}
int max(int L[],int N)
{
	int thissum,maxsum=0;
	int i,j,k=0;
	int left,right;
	for (i=0;i<N ;i++ ){
		thissum = 0;
		if(L[i] <= 0){
            k++;
		}
		for (j=i;j<N ; j++)
		{
			thissum += L[j];
			if(thissum > maxsum){
				maxsum = thissum;
				right = L[j];
				left = L[i];
			}
		}
	}
	if(k == N){
        printf("%d %d %d\n",0,L[0],L[N-1]);
	}else{
        printf("%d %d %d\n",maxsum,left,right);
	}
}