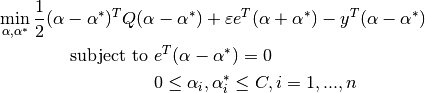scikit-learn学习笔记：1.4 支持向量机（Support Vector Machines）

Support vector machines(SVMs)是一系列监督的学习方法，可以被用于分类、回归和异常值检测。

支持向量机的优点：

• 在高维空间很有效
• 在维度数量远大于样本数量的时候依然很有效
• 在决策函数（通常叫做支持向量）中使用一个训练样本的子集，因此它也记忆很有效率
• 通用的：不同的核（kernel）函数也可以被表述为不同的决策函数。通常kernels是被提供的，但也可以指定自定义kernel。

支持向量机的缺点：

• 如果特征的数量远远高于样本的数量，这个方法似乎性能很差。
• SVMs不能直接提供概率估计，这些的计算使用了一个非常昂贵的5个折叠的交叉验证。（see Scores and probablities, below）

1.4.1 分类

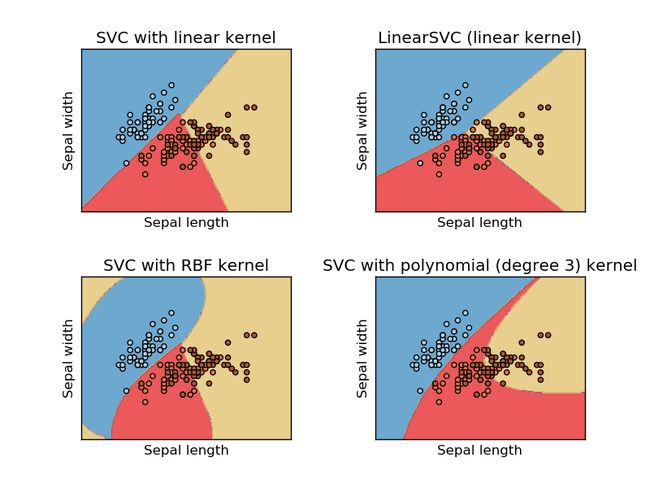
SVC，NuSVC 和 LinearSVC 能在数据集上有多类能力执行多类的分类。

SVC 和 NuSVC 是相似的方法，但是他们的参数集合稍有不同，并且有着不同的数学形式。另一方面， LinearSVC 是对于一个线性kernel情况的支持向量分类的另一个实现。 注意 LinearSVC 不接收关键字 kernel，因为它的假定是线性的。它也缺少一些 SVC 和 NuSVC 的一些成员，如 support_。
至于其他的分类器， SVC，NuSVC 和LinearSVC 有两个arrays的输入：一个尺寸为[n_samples, n_features] 保存训练样本，和一个array的类别标签y，尺寸是[n_samples]：

>>> from sklearn import svm
>>> X = [[0, 0], [1, 1]]
>>> y = [0, 1]
>>> clf = svm.SVC()
>>> clf.fit(X, y)  
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape=None, degree=3, gamma='auto', kernel='rbf',
    max_iter=-1, probability=False, random_state=None, shrinking=True,
    tol=0.001, verbose=False)

在被fitted之后，这个模型就可以对新的值进行预测了：

>>> clf.predict([[2., 2.]])
array([1])

SVMs决策函数依靠训练样本的一些子集，也叫做支持向量。这些支持向量的一些性质可以在成员support_vectors、support_和n_support中被发现。

>>> # get support vectors
>>> clf.support_vectors_
array([[ 0.,  0.],
       [ 1.,  1.]])
>>> # get indices of support vectors
>>> clf.support_ 
array([0, 1]...)
>>> # get number of support vectors for each class
>>> clf.n_support_ 
array([1, 1]...)

1.4.1.1. 多类分类（Multi-class classification）

SVC 和 NuSVC 使用了“one-against-one”方法（Knerr et al.,1990）对于多类目标分类。如果n_class是类别的数目，那么n_class * （n_class - 1）/2个分类器会被构造并且每一个都要从两类数据中经过训练。为了提供与其他分类一致的接口，这个decision_function_shape选项允许集合“one-against-one”分类器的所有结果到一个大小为(n_samples,n_classes)的决策函数中：

>>> X = [[0], [1], [2], [3]]
>>> Y = [0, 1, 2, 3]
>>> clf = svm.SVC(decision_function_shape='ovo')
>>> clf.fit(X, Y) 
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovo', degree=3, gamma='auto', kernel='rbf',
    max_iter=-1, probability=False, random_state=None, shrinking=True,
    tol=0.001, verbose=False)
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes: 4*3/2 = 6
6
>>> clf.decision_function_shape = "ovr"
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes
4

另一方面， LinearSVC 实现了“one-vs-the-rest”多类的策略，这样训练一个n_class个模型。如果仅仅有两个类，仅仅需要训练一个模型：

>>> lin_clf = svm.LinearSVC()
>>> lin_clf.fit(X, Y) 
LinearSVC(C=1.0, class_weight=None, dual=True, fit_intercept=True,
     intercept_scaling=1, loss='squared_hinge', max_iter=1000,
     multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
     verbose=0)
>>> dec = lin_clf.decision_function([[1]])
>>> dec.shape[1]
4

1.4.7. 数学公式（Mathematical formulation）

一个支持向量机在一个高维或者有限维的空间中构建一个超平面或者是一组超平面的集合，这些支持平面可以用于分类、回归或是其他的任务。直观地看，当超平面与任何类的最近的数据距离最大化时，将实现一个最好的分割，通常也被成为函数边界（function margin），因此通常对于分类器来说更大的距离会有更低的泛化误差（the generalization error）。

1.4.7.1. SVC

给一个训练向量 xi∈Rp,i=1,...,n 在两类中，并且一个向量 y∈{1,−1}n ，SVC解决加下来是主要问题：

minw,b,ζ12wTw+C∑i=1nζi

subjecttoyi=(wTϕ(x)+b)≥1−ζi

ζi≥0,i=1,...,n

它的偶是

minα12αTQα−eTα

subjecttoyTα=0

0≤αi≤C,i=1,...,n

1.4.7.2. NuSVC

1.4.7.3 SVR

给一个训练向量 xi∈Rp,i=1,...,n 在两类中，并且一个向量 y∈Rn ， ε−SVC 解决加下来是主要问题：

它的对偶问题是