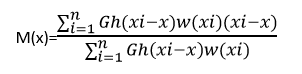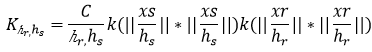基于mean shift的图像分割

1 mean shift算法
Mean Shift 这个概念最早是由Fukunaga 等人[1]于1975 年在一篇关于概率密度梯度函数的估计中提出来的,其最初含义正如其名,就是偏移的均值向量,在这里Mean Shift 是一个名词,它指代的是一个向量,但随着Mean Shift 理论的发展,Mean Shift 的含义也发生了变化,如果我们说Mean Shift 算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,移动该点到其偏移均值,然后以此为新的起始点,继续移动,直到满足一定的条件结束。
然而在以后的很长一段时间内Mean Shift 并没有引起人们的注意,直到20 年以后,也就是1995 年,另外一篇关于Mean Shift 的重要文献[2]才发表.在这篇重要的文献中,Yizong Cheng对基本的Mean Shift 算法在以下两个方面做了推广,首先Yizong Cheng 定义了一簇核函数,使得随着样本与被偏移点的距离不同,其偏移量对均值偏移向量的贡献也不同,其次Yizong Cheng 还设定了一个权重系数,使得不同的样本点重要性不一样,这大大扩大了Mean Shift 的适用范围.另外Yizong Cheng 指出了Mean Shift 可能应用的领域,并给出了具体的例子.
Comaniciu 等人[3][4]把Mean Shift 成功的运用的特征空间的分析,在图像平滑和图像分割中Mean Shift 都得到了很好的应用. Comaniciu 等在文章中证明了,Mean Shift 算法在满足一定条件下,一定可以收敛到最近的一个概率密度函数的稳态点,因此Mean Shift 算法可以用来检测概率密度函数中存在的模态。Comaniciu 等人[5]还把非刚体的跟踪问题近似为一个Mean Shift 最优化问题,使得跟踪可以实时的进行。
1.1mean shift定义

给定d维空间Rd中的n个样本点xi , i=1, … , n, 在x点的Mean Shift向量的基本形式定义为

其中, Sh是一个半径为h的高维球区域, 满足以下关系的y点的集合,

Sh(x)≡ {y∶(y-x)T(y-x)≤ h*h } (2)

其中, k为在这n个样本点xi中, 有k个点落入Sh区域中。(xi-x)是样本点xi相对于点x的偏移向量, 式(1)定义的Mean Shift向量Mh(x)就是对落入区域Sh中的k个样本点相对于点x的偏移向量求和然后再平均。从直观上看, 如果样本点xi从一个概率密度函数f(x)中采样得到, 由于非零的概率密度梯度指向概率密度增加最大的方向, 因此从平均上来说, Sh区域内的样本点更多的落在沿着概率密度梯度的方向。因此, 对应的Mean Shift向量Mh(x)应该指向概率密度梯度的方向。

1.2扩展的mean shift

从(1)式我们可以看出,只要是落入Sh 的采样点,无论其离x 远近,对最终的Mh(x) 计算的贡献是一样的,然而我们知道,一般的说来,离x 越近的采样点对估计x 周围的统计特性越有效,因此我们引进核函数的概念,在计算Mh(x) 时可以考虑距离的影响;同时我们也可以认为在这所有的样本点xi 中,重要性并不一样,因此我们对每个样本都引入一个权重系数.

如此以来我们就可以把基本的MeanShift 形式扩展为:

其中：

           

            G(x)是一个单位核函数

            H是一个正定的对称d*d矩阵

            W(xi)是赋给采样点xi的权重

1.3算法步骤

我们在前面已经指出,我们在提及Mean Shift 向量和Mean Shift 算法的时候指代不同的概念,Mean Shift 向量是名词,指的是一个向量;而Mean Shift 算法是动词,指的是一个迭代的步骤.我们把(2)式的x 提到求和号的外面来,可以得到下式,

 

            

把上式右边第一项记为mh(x)，给定一个初始点x ,核函数G(X ) , 容许误差ε ,Mean Shift 算法循环的执行下面三步,直至结束条件满足,

(1).计算mh(x)

(2).把mh(x) 赋给x

(3).如果 mh (x) − x <ε ,结束循环;若不然,继续执行(1).

由(3)式我们知道, mh( x )= x +Mh( x ),因此上面的步骤也就是不断的沿着概率密度的梯

度方向移动,同时步长不仅与梯度的大小有关,也与该点的概率密度有关,在密度大的地方,更接近我们要找的概率密度的峰值,Mean Shift 算法使得移动的步长小一些,相反,在密度小的地方,移动的步长就大一些.在满足一定条件下,Mean Shift 算法一定会收敛到该点附近的峰值。

 

 

2 mean shift用于图像分割

一幅图像可以表示成一个二维网格点上 p 维向量,每一个网格点代表一个象素, p =1表示这是一个灰度图, p = 3表示彩色图, p > 3表示一个多谱图,网格点的坐标表示图像的空间信息.我们统一考虑图像的空间信息和色彩(或灰度等)信息,组成一个 p + 2 维的向量x = (xs ,xr ) ,其中xs表示网格点的坐标, xr 表示该网格点上p 维向量特征。我们用核函数来估计x的分布， 具有如下形式

其中,hr、hs  控制着平滑的解析度,C 是一个归一化常数。

我们分别用xi 和zi ,i=1,…,n 表示原始和平滑后的图像.用Mean Shift 算法进行图像平滑的具体步骤如下,

对每一个象素点,

1,初始化 j =1,并且使

2,运用 Mean Shift算法计算  ,直到收敛.记收敛后的值为

3.赋值

  基于Mean Shift 的图像分割与图像平滑非常类似,只需要把收敛到同一点的起始点归为一类,然后把这一类的标号赋给这些起始点,这其实也是一种聚类方法。在图像分割中有时还需要把包含象素点太少类去掉[7]。

在基于Mean Shift 的图像分割中,式(28)中的,  是非常重要的参数,人们可以根据解析度的要求而直接给定,不同, 会对最终的分割结果有一定的影响,实验结果显示了这两个参数对平滑结果的影响,在后面我们可以看出, 影响更大一些。

效果

            

左图为原图，右图为mean shift分割效果