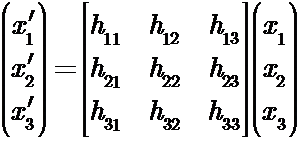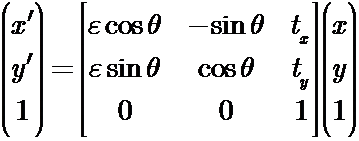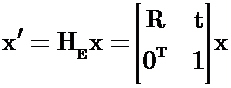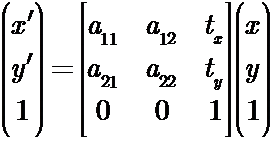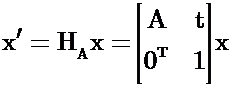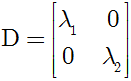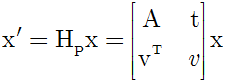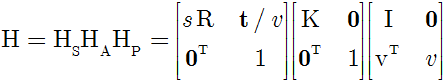仿射变换和仿射线性群
2D射影几何研究的是关于射影平面IP2在射影映射的变换群下保持不变的性质.
射影映射是IP2到它自身的一种满足下列条件的可逆映射h: 三点x1, x2和x3共线当且仅当h(x1),h(x2), h(x3) 也共线.
射影映射是把IP2的点 (即齐次三维矢量) 映射到IP2的点的一种可逆映射, 它把直线映射到直线. 射影映射也称为保线变换, 或射影变换 (projective transformation) 或单应 (homography).
平面射影变换是关于齐次三维矢量的一种线性变换,可用一个3×3非奇异矩阵H表示为:
或者更简洁地表示为x’ = Hx. 注意矩阵H乘以任意一个非零比例因子不会使射影变换改变. 换句话说H是一个齐次矩阵, 与点的齐次表示一样, 有意义的仅仅是矩阵元素的比率. 在H的九个元素中有8个独立比率, 因此一个射影变换有8个自由度.
平面之间的映射. 沿一个公共点(投影中心) 的射线的投影定义了从一张平面到另一张平面上的映射 (参考射影平面的定义).
在透视影像下形状会失真. 例如实际中景物平面上的平行线在图像上一般地不平行并会聚到一个有限点. 由于平面(部分平面)的中心投影的图像与原平面通过射影变换相关, 因而该图像是原景物的一种射影失真. 通过求该射影变换的逆变换并把它应用于图像就有可能“撤销”此射影变换. 它的结果将是一幅新的合成图像, 其中在此平面上的物体将显示在其正确的几何形状. 一般地, 四组点对应提供8个关于矩阵H元素的线性方程, 并足以解出H (仅相差一个不重要的乘法因子). 唯一的限制是这四点必须在“一般位置”上, 即要求没有三个点共线.
前面介绍到射影变换组成一个群, 这个群被称为射影线性群. 射影线性群的重要子群包括仿射群和欧式群, 仿射群是由射影线性群的最后一行为(0, 0, 1) 的矩阵组成的子群, 欧式群是仿射群的子群, 其左上角的2×2矩阵是正交的. 当左上角的2×2矩阵的行列式为1时称为定向欧式群.
1. 等距变换 (isometric)
其中ɛ=±1. 如果ɛ=1 那么该等距变换是保向的并且也是欧式变换(平移和旋转的复合). 如果ɛ=-1 那么该等距变换是逆向的. 欧式变换是刚体运动的模型.不变量包括长度, 角度和面积. 自由度为3. 平面欧式变换可以用更简洁的分块形式写为
2. 相似变换
相似变换是一个等距变换与一个均匀缩放的复合. 当欧式变换(没有反射)与均匀缩放复合时, 相似变换的矩阵表示为
可以更简洁的分块表示为
自由度为4个, 比欧式变换多一个缩放自由度. 相似变换可以由两组点对应算出.不变量为角度, 两长度的比率, 面积的比率.
3. 仿射变换
仿射变换是一个非奇异线性变换与一个平移变换的复合, 它的矩阵表示为
或分块形式
A是一个2×2的非奇异矩阵(满秩). 平面仿射变换有6个自由度, 对应于6个矩阵元素. 变换可以由三组对应点算出. 理解仿射变换的几何效应的一个有益方法是把它看作两个基本变换--旋转和非均匀缩放的复合. 仿射变换A总能分解为
其中R(θ)和R(ϕ)分别表示转角为θ和ϕ的旋转, 而D为对角矩阵
推导过程为A=UDVT=(UVT)(VDVT)=R(θ)R(-ϕ)DR(ϕ), 其中第一个等式来自于A的SVD分解, 其他等式则因为U和V是正交矩阵. 因此, 仿射矩阵A被看作一个旋转ϕ, 加上在(已旋转)的x和y方向分别进行按比例因子λ1和λ2的缩放, 再加上一个回转-ϕ和最后一个旋转θ的复合变换. 与相似变换相比, “新”几何仅仅是非均匀缩放, 多了两个自由度分别是缩放方向的角度ϕ和缩放参数比率λ1: λ2. 不变量包括平行线, 平行线段的长度比, 面积比.
4. 射影变换
其中矢量v=(v1,v2)T . 齐次矩阵虽有九个元素但只有它们的比率是有意义的, 因此该变换由8个参数确定. 注意并不是总有可能通过对矩阵缩放而取v为1, 因为v可能是零. 两平面之间的射影变换可由四组点对应算出, 但其中属于同一平面的三点必须不共线. 最基本的射影不变量是四共线点的交比: 直线上长度的比率在仿射变换下保持不变, 但在射影变换下并非如此. 然而比率的比率及直线上长度的交比是射影不变量.
射影变换可以分解为一串变换链的复合, 链中每个矩阵比它前面的矩阵所表示的变换层次高.
其中A=sRK+tvT/v, 而K是满足det K=1 的归一化上三角矩阵. 如果上述分解是有效的, 而且如果s取正值, 它还是唯一的.