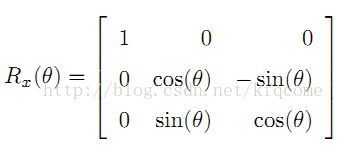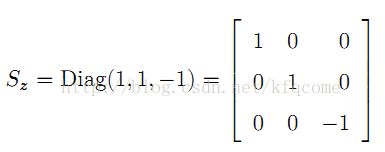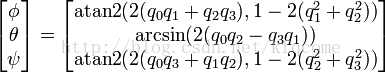三维旋转基础
一 旋转矩阵
旋转矩阵(右手坐标系)
绕X轴旋转
绕Y轴旋转
绕Z轴旋转
绕某个向量v绕XYZ旋转x,y,z进行旋转。v’ = Rz*Ry*Rx*v;
Matlab代码如下
syms sinx cosx siny cosy sinz cosz;
Rx = [1 0 0;0 cosx -sinx;0 sinx cosx];
Ry = [cosy 0 siny;0 1 0;-siny 0 cosy];
Rz = [cosz -sinz 0;sinz cosz 0;0 0 1];
R = Rz*Ry*Rx
输出:
R =
[ cosy*cosz, cosz*sinx*siny - cosx*sinz, sinx*sinz + cosx*cosz*siny]
[ cosy*sinz, cosx*cosz + sinx*siny*sinz, cosx*siny*sinz - cosz*sinx]
[ -siny, cosy*sinx, cosx*cosy ]
二 旋转矩阵含义
以绕Y轴进行旋转为例,绕Y轴旋转对应的矩阵是
[ cosy, 0, siny]
Ry= [ 0, 1, 0 ]
[ -siny, 0, cosy]
从-Y轴方向看绕Y的旋转:
经过旋转后,Z轴的方向向量变成了(sin(ry),0,cos(ry)),X轴的方向向量变成了(cos(ry),0,-sin(ry)),而Y的方向向量仍然是(0,1,0)。可以发现,旋转后的新的三个坐标轴向量即为对应旋转矩阵的三个列向量。
使用旋转矩阵对一个向量进行旋转
[ cosy, 0, siny] [x] [x’]
Ry*v= [ 0, 1, 0 ] *[y] = [y’]
[ -siny, 0, cosy] [z] [z’]
旋转的实质就是相当于在新的坐标系下,保持该点在新的坐标系下的坐标仍然为(x,y,z),在新的坐标系的坐标为(x,y,z),那么在原先的坐标系下的点的坐标即为Ry*v。
三 左手坐标系向右手坐标系转换
可以看出,从左手坐标系到右手坐标系转换,只需将z值取反即可。
以Qr为右手坐标系的一点,Ql为对应的左手坐标系的点,转换公式如下
转换矩阵Sz如下
现在进行旋转矩阵转换的推导
假如ML为如下矩阵,
[ a00, a01, a02]
ML = [ a10, a11, a12]
[ a20, a21, a22]
则对应的MR为
[ a00, a01,-a02]
MR = [ a10, a11,-a12]
[ -a20,-a21, a22]
即红色标出的成员被取反。
四 四元数到旋转角的转化
四元数q=[w x y z],w用来表示旋转量,(x,y,z)则是旋转轴。
四元数相乘:
q1 * q2 =
(w1*w2 - x1*x2 - y1*y2 - z1*z2) +
(w1*x2 + x1*w2 + y1*z2 - z1*y2) i +
(w1*y2 - x1*z2 + y1*w2 + z1*x2) j +
(w1*z2 + x1*y2 - y1*x2 + z1*w2) k
将四元数应用于一个向量使之旋转,将这个向量v也用四元数表示,v=[0 vx vy vz],旋转的计算式为:![]()
同时也可以将四元数的旋转用矩阵形式表示,对应的旋转矩阵
同时,使用一组欧拉角,也能计算出对应的旋转矩阵
R = Rz*Ry*Rx=
[ cosy*cosz, cosz*sinx*siny - cosx*sinz, sinx*sinz + cosx*cosz*siny]
[ cosy*sinz, cosx*cosz + sinx*siny*sinz, cosx*siny*sinz - cosz*sinx]
[ -siny, cosy*sinx, cosx*cosy ]
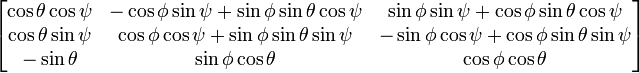
![]() 分别为绕X、Y、Z轴旋转的角度,也就是对应上式R中的x、y、z。得出如下的转换公式:
分别为绕X、Y、Z轴旋转的角度,也就是对应上式R中的x、y、z。得出如下的转换公式:
rx= atan2(Mq[2][1],Mq[2][2]),
ry = arcsin(Mq[2][0]);
rz= atan2(Mq[1][0],Mq[0][0]
也就是如下的计算式
五 三角函数
1 asin函数
它的结果范围是-PI/2到PI/2,使用matlab进行绘图可得
x=[-1:0.05:1];
y = asin(x);
plot(x,y);

2 acos函数
它的取值范围是0到PI
x=[-1:0.05:1];
y = acos(x);
plot(x,y);
3 atan2函数
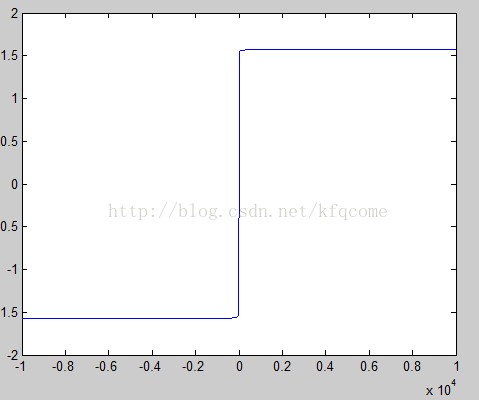
它的取值范围是-PI/2到PI/2
y=[-10000:1:10000];
x = ones(1,length(y));
rad = atan2(y,x);
plot(y,rad);
结果图如下: