POJ1149 PIGS
题意:M(1 <= M <= 1000)个猪圈,n(1 <= n <= 100)个顾客,每个顾客打开指定的猪圈,有购买的上限,打开的猪圈的猪,可以随便跑到其他开着的猪圈里,然后猪圈重新关上,问总共卖出多少头猪。
分析:
这题基本上一看就是个网络流,重点在建模。
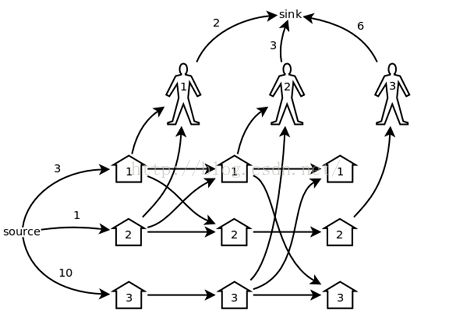
我们先来想一个暴力的建图:
每个顾客创建m个点,表示猪圈。
以样例来说,暴力建完图后如下。
这个东西有点复杂,我们来简化一下。
首先,如果某个点无法直接或间接的到汇点,直接删掉。
然后:
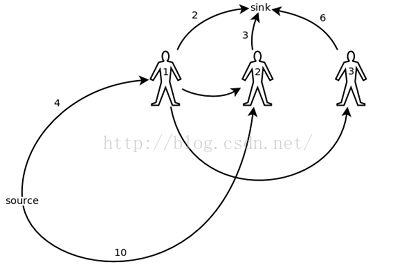
最终,这个图被简化成如下样子:
看着清爽了许多...
考虑一下实现方法。
然后就是模板网络流了。
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
const int N = 105, M = 300000, MM = 1005, inf = 0x3fffffff;
int n,m,s,t,x,y,e,w[MM],vis[MM],hd[N],nxt[M],f[M],to[M],ch[N];
vector<int> v[MM];
void add(int x, int y, int z) {
to[e] = y, f[e] = z, nxt[e] = hd[x], hd[x] = e++;
to[e] = x, f[e] = 0, nxt[e] = hd[y], hd[y] = e++;
}
bool tell() {
memset(ch, -1, sizeof ch);
queue<int> q;
q.push(s);
ch[s] = 0;
while(!q.empty()) {
int u = q.front(); q.pop();
for(int i = hd[u]; ~i; i = nxt[i]) if(ch[to[i]] == -1 && f[i])
ch[to[i]] = ch[u] + 1, q.push(to[i]);
}
return ch[t] != -1;
}
int zeng(int a, int b) {
if(a == t) return b;
int r = 0;
for(int i = hd[a]; ~i && b > r; i = nxt[i]) if(ch[to[i]] == ch[a] + 1 && f[i]) {
int t = zeng(to[i], min(b-r, f[i]));
f[i] -= t, r += t, f[i^1] += t;
}
return r;
}
int dinic() {
int r = 0, t;
while(tell()) while(t = zeng(s, inf)) r += t;
return r;
}
int main() {
scanf("%d%d", &m, &n), t = n+1;
memset(hd, -1, sizeof hd);
for(int i = 1; i <= m; i++) scanf("%d", &w[i]);
for(int i = 1; i <= n; i++) {
scanf("%d", &x);
while(x--) {
scanf("%d", &y);
if(!vis[y]) vis[y] = 1, add(s, i, w[y]);
v[y].push_back(i);
}
scanf("%d", &x), add(i, t, x);
}
for(int i = 1; i <= m; i++)
for(int j = 1; j < v[i].size(); j++)
add(v[i][j-1], v[i][j], inf);
printf("%d\n", dinic());
return 0;
}