POJ1160 Post Office（经典DP）

题目点我点我点我

题目大意：在V个村庄建立P个邮局，求每个村庄到邮局的最短距离总和。

解题思路：经典DP问题。

DP问题经常是从子问题推及到父问题，此题也如此。

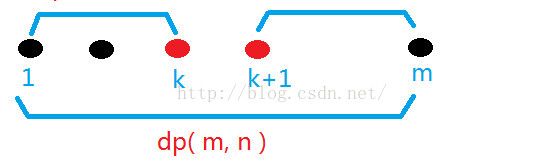
假设现有m个村庄V1、V2、V3……Vm，要建立n个邮局，P1、P2……Pm，

先考虑建立有个邮局的情况，假设第k+1个村庄到第m个村庄只有一个邮局，

那么，剩下的n-1个邮局都在V1到Vk村庄中，所以：

sum[i][j]表示从第i个村庄到第j个村庄只有一个邮局的距离总数；

dp[i][j]表示从第1个村庄到第j个村庄有i个邮局的距离总数；

按照上述思路，就有了下面的状态转移方程：

dp[i][j]=min(dp[i][j],dp[i-1][k]+sum[k+1][j]);

顺手盗个图理解一下：

现在的问题就是如何求sum[i][j]了。

显然，只有一个邮局的情况下，在i到j的中点建立距离和是最短的。所以可得：

sum[i][j]=sum[i][j-1]+d[j]-d[(i+j)/2];

d[i]表示第i个村庄的位置。

/* ***********************************************
┆  ┏┓　　　┏┓ ┆
┆┏┛┻━━━┛┻┓ ┆
┆┃　　　　　　　┃ ┆
┆┃　　　━　　　┃ ┆
┆┃　┳┛　┗┳　┃ ┆
┆┃　　　　　　　┃ ┆
┆┃　　　┻　　　┃ ┆
┆┗━┓　马　┏━┛ ┆
┆　　┃　勒　┃　　┆　　　　　　
┆　　┃　戈　┗━━━┓ ┆
┆　　┃　壁　　　　　┣┓┆
┆　　┃　的草泥马　　┏┛┆
┆　　┗┓┓┏━┳┓┏┛ ┆
┆　　　┃┫┫　┃┫┫ ┆
┆　　　┗┻┛　┗┻┛ ┆
************************************************ */

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <string>
#include <math.h>
#include <stdlib.h>
using namespace std;

#define rep(i,a,b) for (int i=(a),_ed=(b);i<_ed;i++)
#define per(i,a,b) for (int i=(b)-1,_ed=(a);i>=_ed;i--)
#define inf 0x3f3f3f3f
#define mod 1000000007
#define ll long long
#define ull unsigned long long


#if ( ( _WIN32 || __WIN32__ ) && __cplusplus < 201103L)
    #define lld "%I64d"
#else
    #define lld "%lld"
#endif

int sum[305][305];  //sum[i][j]表示从第i个村庄到第j个村庄只有一个邮局的距离总数
int dp[305][305];   //dp[i][j]表示从第1个村庄到第j个村庄有i个邮局的距离总数
int v,p;
int d[305];


int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
	while(~scanf("%d%d",&v,&p))
    {
        for(int i=1;i<=v;i++)
        {
            scanf("%d",&d[i]);
        }
        memset(sum,0,sizeof sum);
        for(int i=1;i<=v;i++)
        {
            for(int j=i+1;j<=v;j++)
            {
                sum[i][j]=sum[i][j-1]+d[j]-d[(i+j)>>1];
            }
        }
        memset(dp,inf,sizeof dp);
        for(int i=1;i<=v;i++)
        {
            dp[1][i]=sum[1][i];
        }
        for(int i=2;i<=p;i++)
        {
            for(int j=1;j<=v;j++)
            {
                for(int k=1;k<j;k++)
                {
                    dp[i][j]=min(dp[i][j],dp[i-1][k]+sum[k+1][j]);
                }
            }
        }
        cout<<dp[p][v]<<endl;
    }
    return 0;
}