STL---heap概述,make_heap,sort_heap,pop_heap,push_heap

heap并不属于STL容器组件，它分为 max heap 和min heap，在缺省情况下，max-heap是优先队列（priority queue）的底层实现机制。

而这个实现机制中的max-heap实际上是以一个vector表现的完全二叉树（complete binary tree）。

二叉堆（binary heap）就是i一种完全二叉树。也即是。整棵二叉树除了最底层的叶节点以外，都是填满的，而最低层的叶子结点必须是从左到右不留空隙。

至于max-heap和min-heap，前者的任何一个父亲结点都必须大于等于他的任意子结点，而后者相反。

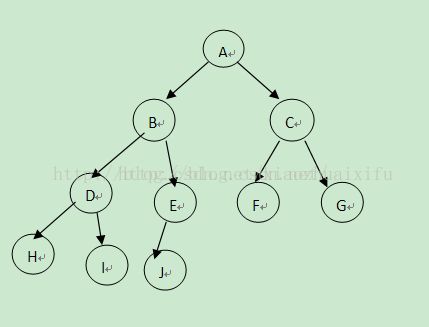
上面表示的是一颗完全二叉树。

下面我们利用数组来隐式表达这棵数：

第0号元素保留，从arry[1]开始保存A，这时候我们可以轻易的看到：

位于位置i的某个结点arry[i]，他的左子结点必然在arry[2*i]中，右子结点必然位于arry[2*i+1]，其父亲结点必然位于arry[i/2]处。

这种数组表达的方式我们 称为 隐式表达。

当然由于arry大小是静态的，不能动态添加元素，我们可以使用vector来实现。

heap-算法：

push_heap()：新添加一个元素在末尾，然后重新调整堆序。也就是把元素添加在底层vector的end()处。

该算法必须是在一个已经满足堆序的条件下，添加元素。该函数接受两个随机迭代器，分别表示first,end,区间范围。

关键是我们执行一个siftup()函数，上溯函数来重新调整堆序。具体的函数机理很简单，可以参考我的编程珠玑里面堆的实现的文章。

pop_heap()这个算法跟push_heap类似，参数一样。不同的是我们把堆顶元素取出来，放到了数组或者是vector的末尾，用原来末尾元素去替代，

然后end迭代器减1，执行siftdown()下溯函数来重新调整堆序。

注意算法执行完毕后，最大的元素并没有被取走，而是放于底层容器的末尾。如果要取走，则可以使用底部容器（vector）提供的pop_back()函数。

sort_heap（）算法：

既然每次pop_heap可以获得堆中最大的元素，那么我们持续对整个heap做pop_heap操作，每次将操作的范围向前缩减一个元素。

当整个程序执行完毕后，我们得到一个非降的序列。

同理，sort_heap(RamdomAccessIteraor first,RamdomAccessIteraor end)接受两个随机迭代器作为参数。表示操作的范围。

注意这个排序执行的前提是，在一个堆上执行。

make_heap()算法：

建立一个堆。很简单吧。接受的参数同上。

下面我们来看测试实例吧：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
	int ia[9]={0,1,2,3,4,8,9,3,5};
	vector<int> ivec(ia,ia+9);  //底层我们使用vector来实现，可以动态添加元素。 
	
	make_heap(ivec.begin(),ivec.end());
	for(int i=0;i!=ivec.size();i++)cout<<ivec[i]<<" ";
	cout<<endl;
	
	ivec.push_back(7);
	push_heap(ivec.begin(),ivec.end());//这里可以用make_heap替换。 
	for(int i=0;i!=ivec.size();i++)cout<<ivec[i]<<" ";
	cout<<endl;
	
	pop_heap(ivec.begin(),ivec.end());
	cout<<ivec.back()<<endl;
	ivec.pop_back();
	for(int i=0;i!=ivec.size();i++)cout<<ivec[i]<<" ";
	cout<<endl;
	
	sort_heap(ivec.begin(),ivec.end());
	for(int i=0;i!=ivec.size();i++)cout<<ivec[i]<<" ";
	cout<<endl;
	////////////////////////////////////////////////////
	{
		int ia[9]={0,1,2,-1,4,8,9,3,5};//底层我使用数组来完成。 
		make_heap(ia,ia+9);
		for(int i=0;i<9;i++)cout<<ia[i]<<" ";
		cout<<endl;
		sort_heap(ia,ia+9);
		for(int i=0;i<9;i++)cout<<ia[i]<<" ";
		cout<<endl;
	}
	
	
	return 0;
}