POJ_1611(The Suspects)

题目链接：http://poj.org/problem?id=1611

这道题的题意是将与0号人在同一组的人数统计出来！

可以看成是与0号组的集合，我们最后统计这个集合的人数有多少就可以。而在并查集中，统计一个组的人数有多少，找到该组的根，然后遍历所有结点，如果它的根序号与我们指定组的根一样，那么数量就加1，最后输出结果就行！

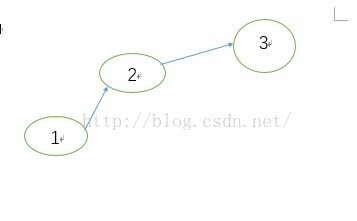
我犯了一个错误，统计组内个数的时候，用了pre[i]是否等于pre[0]去了！应该用findd(i)是否等于findd(0)，因为findd()函数才找到了它的根，而pre只是找到它的父亲，如果还没有进行路径压缩的话，不一定同一组的俩个结点的父亲结点是相同的！如下图：

在上图中，如果还没有查询到1，那么就还没有进行路径压缩（因为路径压缩操作是在findd()函数中递归实现）,那么即使这是在一个集合中的元素！1的父亲结点是2,2的父亲结点是3，那么你根据父亲结点来判断是否在一个集合中，是不对的！而通过找根结点来判断的话，同一组中根结点序号都是3，那么我们就找到了!!

ac代码如下：

#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#include <stack>
#include <queue>
#include <map>
#include <vector>
#include <cmath>
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
const int maxn = 35555;
int pre[maxn];
void init()
{
	for (int i = 0; i<maxn; i++)
		pre[i] = i;
}

int findd(int i)
{
	if (i == pre[i])
		return i;
	else
		return pre[i] = findd(pre[i]);
}
void unionn(int i, int j)
{
	int fi = findd(i);
	int fj = findd(j);
	pre[fi] = fj;                                   //俩个集合之间的连接
}
int main(void)
{
	//freopen("in.txt", "r", stdin);                 //这道题就是在统计与0号人员在一组的组内组员个数
	int n, m;

	while (scanf("%d%d", &n, &m) != EOF)
	{
		if (n == 0 && m == 0)
			break;
		init();
		int k, i, j, x, y;                                       
		for (int ii = 0; ii < m; ii++)
		{
			scanf("%d", &k);
			scanf("%d", &x);
			for (i = 1; i < k; i++)
			{
				scanf("%d", &y);
				unionn(x, y);                                  //都与第一个为一组,集合之间的融合
			}
		}
		//下面统计0号组有多少个，就是看与0有一样的父亲的结点有多少个，就能判断有多少个跟0是一组的
		int sum = 0;
		for (i = 0; i<n; i++)
		{
			//if (pre[i] == pre[0])                              //跟0号是一组的情况下
				//sum++;                                         这个判断是打错特错啊，因为你判断是否在一个集合，并不是看它的父亲结点是否相同(因为有可能还没有经过findd路径压缩)，而是看他们查找到的最终根结点是否相同
			if (findd(i) == findd(0))
				sum++;
		}
		printf("%d\n", sum);
	}
	return 0;
}