摄像机模型与标定——摄像机标定
摄像机的外参数:旋转向量(大小为1×3的矢量或旋转矩阵3×3)和平移向量(Tx,Ty,Tz)。
这里我们讲解一下旋转向量:
旋转向量是旋转矩阵紧凑的变现形式,旋转向量为1×3的行矢量。
上述公式中r就是旋转向量,1、旋转向量的方向是旋转轴 2、旋转向量的模为围绕旋转轴旋转的角度。通过上面的公式三,我们就可以求解出旋转矩阵R。同样的已知旋转矩阵,我们也可以通过下面的公式求解得到旋转向量: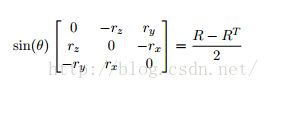
内参数(fx,fy,cx,cy)与棋盘所在空间的3D几何相关(即外参数),畸变参数则与点集如何畸变的2D几何相关。
1、5个畸变系数的求解:已知模式(我们可以认为是黑色方格,含有四个角点)的三个角点所产生的6组信息(在理论上)可以求解5个畸变参数。
2、内参数fx,fy,cx,cy,和(ψ,φ,θ),(Tx,Ty,Tz)共10个参数的求解将在下面详细讲述。
首先说明:求解上述2中10个参数的前提是先假设每次的畸变参数为0。
求解4个内参数和6个外参数的分析:
假设有N个角点和K个棋盘图像(不同位置),需要多少个视场和角点才能提供足够的约束来求解这些参数呢?
1、K个棋盘,可以提供2NK的约束,即2NK的方程。(乘以2是因为每个点都由x和y两个坐标值组成)
2、忽略每次的畸变,那么我们需要求解4个内参数和6K个外参数。(因为对于不同的视场,6个外参数是不同的)
3、那么有解的前提是方程的总数应该大于等于未知参数的总数即2NK>=6K+4,或者写成(N-3)K>=2。
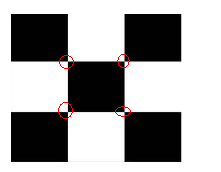
为了方便理解,下图是一个3×3大小的棋盘,红色圈标记出了它含有的内角点:
如果我们令N=5,K=1,带入到上述不等式,是满足不等式,这就是意味着我们仅需要一个视场和带有5个内角点的棋盘就可以求解出10个参数了。其实不然,为了描述投影视场的所有目标只需要4个点,即一次性在四个方向上延展正方形的边,把它变成任意四边形。因此,无论一个平面上检测到多少个角点,我们只能得到4个有用的角点信息。如上图所示是一个3×3大小的棋盘,有4个内角点。
对于每一个视场,我们仅能给出4个有用的角点信息,那么上述的公式中K就约束为4,即公式变为(4-3)K>=2,即K>=2。即要求解10个参数最少需要两个视场。
考虑到噪声和数值稳定性要求,对大棋盘需求收集更多的图像。
为了得到高质量结果,至少需要10幅7×8或者更大棋盘的图像(而且只在移动棋盘在不同图像中足够大以从视场图像中得到更加丰富的信息)。
数学是怎么应用于标定的?
OpenCV选着那些能够很好工作于平面物体的方法。OpenCV中使用的求解焦距和偏移的算法是基于张的方法,但求解畸变参数则是另外一个基于Brown的方法。
首先我们假定求解标定参数时,摄像机没有畸变。对于每一个棋盘视场,我们得到一个前面描述的单应性矩阵H,大小为3×3。将H写成列向量的形式,即H=[h1 h2 h3],每个h是3×1向量,根据前面单应性的介绍,我们知道单应性矩阵H是物理变换(旋转、平移)和相机内参数组成。我们的目的就是分解这个H,能够从中分解出这些成分。由单应性一节,我们知道:
我们知道R=[r1,r2,r3],r3消失,是因为我们另Z=0。R是一个正交阵,即R的转置等于R的逆。正交阵的每个列向量是两两正交且单位化的(即模为1),那么r1和r2是相互正交。
正交的含义有两个:两个矢量的点积为0,两个矢量的长度相等。下面我们就用这两个约束来进行求解。
另:
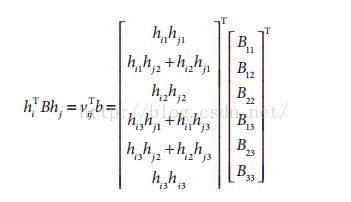
由于B是对称真,那么B可以仅有对角线下半元素或者对角线上半元素表示,即可以有6个元素表示。我们将通用形式展开,并且提取出B成分,那么通用形式可以写成含有旋转成分和含有B成分的6个元素组成的向量的点积(注意:是点积,不是两个矩阵相乘),如下:
从上述公式,我们已知单应性矩阵H,那么它其中的每一个元素我们都是已知的,那么上述Bij是我们要求解的值,公式:即可以理解为:a1x1+a2x2+a3x3..+a6x6=0,等式的求解。
我们可以组合两个约束为如下的形式:
从上述可知对于每一个视场我们可以得到形如上面描述的2个公式(上述黄色部分),那么对于K的视场,我们可以得到2K个这样的公式。
我们堆积这些方程有:
Vb=0
那么b是要求解未知数矢量大小为6×1,V是2K×6的矩阵,如果K>=2,那么方程有解b=[B11,B12,B22,B13,B33]T,看到这里,你或许会晕一下,我们要求解B,B是一个含有6个元素的矢量,而当K=2时,我们只能获得4个方程呀?其实,我们忘了一点,那就是内参数矩阵中只有4个未知数,四个方程,4个未知数,那么就可以求解出cx,cy,fx,fy,而b就是由这四个参数组合而成的。摄像机内参数可以从B矩阵的封闭解中直接得到:
上述公式中,λ,M,H,都是求解的得到的作为已知量,r3=r1×r2,这是因为r1,r2,r3两两正交。
需要小心的是,当我们使用真实的数据求解时,将计算得到的r向量放在一起(R=(r1,r2,r3)),我们并不能得到精确的旋转矩阵R,使得R为正交阵。
为了解决这个问题,我们常使用强制的方法,即对R进行奇异值分解,R=UDVT,U,V为正交阵,D为对角阵,如果R是正交阵,那么奇异值分解后的对角阵D是单位阵,那么我们将单位阵I代替对角阵D,进而重构出满足正交条件的R.
处理透镜畸变
在前面的工作中,我们总是先忽略透镜畸变,然后求解得到的系统。如果针孔模型是完美的,另(xp,yp)为点的位置,令(xd,yd)为畸变的位置,那么有:
就像先前描述的那样,上述5个畸变参数:k1,k2,k3,p1,p2,需要3个角点构成的6组方程就可以求解。我们猜测一下,上述第一个公式,我们通过前面的计算已经求解出相机的内参数:fx,fy,cx,cy,棋盘平面上角点的坐标为世界坐标,其中X,Y我们可以理解为在其平面上的坐标,Z是一个尺度,因为我们知道求解单应性矩阵H,也是一个尺度,所以具体怎么控制,先不用管,我们就可以通过上述公式一求解出xp和yp,xd,yd就是成像仪上角点的真实位置,那么就可以由xp,yp和xd,yd的点对,带入到上述的公式二,求可以求解出5个畸变系数。