Mean Shift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,移动该点到其偏移均值,然后以此为新的起始点,继续移动,直到满足一定的条件结束.
1. Meanshift推导
给定d维空间Rd的n个样本点 ,i=1,…,n,在空间中任选一点x,那么Mean Shift向量的基本形式定义为:

Sk是一个半径为h的高维球区域,满足以下关系的y点的集合,

k表示在这n个样本点xi中,有k个点落入Sk区域中.
以上是官方的说法,即书上的定义,我的理解就是,在d维空间中,任选一个点,然后以这个点为圆心,h为半径做一个高维球,因为有d维,d可能大于2,所以是高维球。落在这个球内的所有点和圆心都会产生一个向量,向量是以圆心为起点落在球内的点位终点。然后把这些向量都相加。相加的结果就是Meanshift向量。
如图所以。其中黄色箭头就是Mh(meanshift向量)。
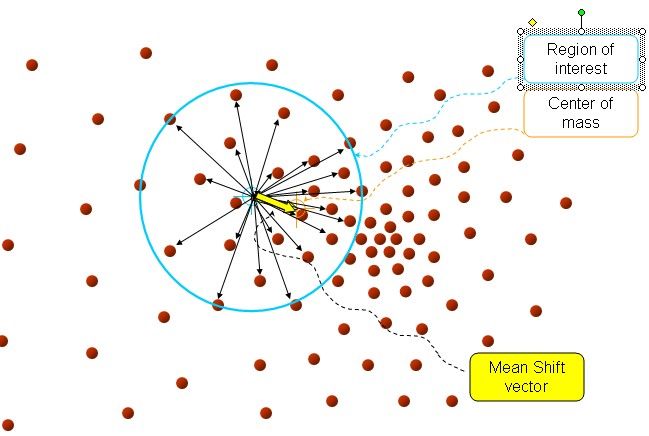
再以meanshift向量的终点为圆心,再做一个高维的球。如下图所以,重复以上步骤,就可得到一个meanshift向量。如此重复下去,meanshift算法可以收敛到概率密度最大得地方。也就是最稠密的地方。
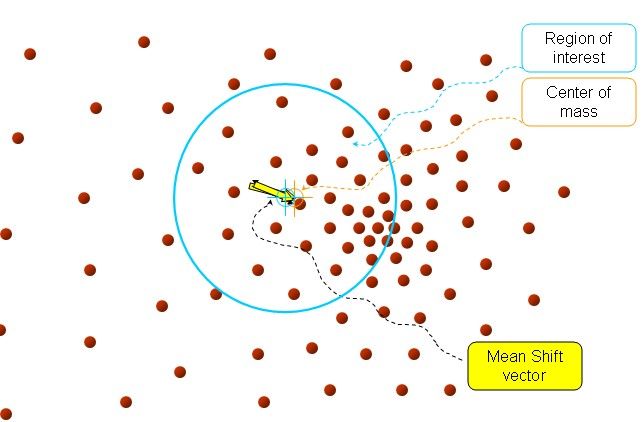
最终的结果如下:

Meanshift推导:
把基本的meanshift向量加入核函数,核函数的性质在这篇博客介绍:http://www.cnblogs.com/liqizhou/archive/2012/05/11/2495788.html
那么,meanshift算法变形为
(1)
解释一下K()核函数,h为半径,Ck,d/nhd 为单位密度,要使得上式f得到最大,最容易想到的就是对上式进行求导,的确meanshift就是对上式进行求导.
(2)
令:

K(x)叫做g(x)的影子核,名字听上去听深奥的,也就是求导的负方向,那么上式可以表示

对于上式,如果才用高斯核,那么,第一项就等于fh,k
第二项就相当于一个meanshift向量的式子:

那么(2)就可以表示为
下图分析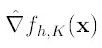 的构成,如图所以,可以很清晰的表达其构成。
的构成,如图所以,可以很清晰的表达其构成。

要使得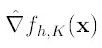 =0,当且仅当
=0,当且仅当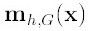 =0,可以得出新的圆心坐标:
=0,可以得出新的圆心坐标:
(3)
上面介绍了meanshift的流程,但是比较散,下面具体给出它的算法流程。
- 选择空间中x为圆心,以h为半径为半径,做一个高维球,落在所有球内的所有点xi
- 计算
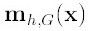 ,如果
,如果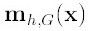 <ε(人工设定),推出程序。如果
<ε(人工设定),推出程序。如果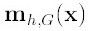 >ε, 则利用(3)计算x,返回1.
>ε, 则利用(3)计算x,返回1.
2.meanshift在图像上的聚类:
真正大牛的人就能创造算法,例如像meanshift,em这个样的算法,这样的创新才能推动整个学科的发展。还有的人就是把算法运用的实际的运用中,推动整个工业进步,也就是技术的进步。下面介绍meashift算法怎样运用到图像上的聚类核跟踪。
一般一个图像就是个矩阵,像素点均匀的分布在图像上,就没有点的稠密性。所以怎样来定义点的概率密度,这才是最关键的。
如果我们就算点x的概率密度,采用的方法如下:以x为圆心,以h为半径。落在球内的点位xi 定义二个模式规则。
(1)x像素点的颜色与xi像素点颜色越相近,我们定义概率密度越高。
(2)离x的位置越近的像素点xi,定义概率密度越高。
所以定义总的概率密度,是二个规则概率密度乘积的结果,可以(4)表示

(4)
其中: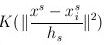 代表空间位置的信息,离远点越近,其值就越大,
代表空间位置的信息,离远点越近,其值就越大, 表示颜色信息,颜色越相似,其值越大。如图左上角图片,按照(4)计算的概率密度如图右上。利用meanshift对其聚类,可得到左下角的图。
表示颜色信息,颜色越相似,其值越大。如图左上角图片,按照(4)计算的概率密度如图右上。利用meanshift对其聚类,可得到左下角的图。
http://www.cnblogs.com/liqizhou/archive/2012/05/12/2497220.html
Matlab中meanshift算法
mean-shift 的特点是把支撑空间和特征空间在数据密度的框架下综合了起来。对图像来讲,支撑空间就是像素点的坐标,特征空间就是对应像素点的灰度或者RGB三分量。将这两个空间综合后,一个数据点就是一个5维的向量:[x,y,r,g,b]。
这在观念上看似简单,实质是一个飞跃,它是mean-shift方法的基点。
mean-shift方法很宝贵的一个特点就是在这样迭代计算的框架下,求得的mean-shift向量必收敛于数据密度的局部最大点。可以细看[ComaniciuMeer2002]的文章。
写了点程序,可以对图像做简单的mean-shift filtering,供参考:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [DRGB, DSD, MSSD] = MScut(sMode, RGB_raw, hs, hf, m );
% designed for segmenting a colour image using mean-shift [ComaniciuMeer 2002]
% image must be color
% procedure in mean-shift
% 1. combine support space and feature space to make a mean-shift space
% based data description
% 2. for every mean-shift space data
% 3. do mean-shift filtering
% until convergence
% 4. end
% 5. find the converged mean-shift space data that you are interested in
% and label it
% 6. repeat the above steps
%
% a -- data in support space
% b -- data in feature space
% x -- data in mean-shift space
% f(.) -- data density function
% k(.) -- profile function (implicit)
% g(.) -- profile function (explicit)
% m -- mean shift vector
% hs -- bandwidth in support space
% hf -- bandwidth in feature space
% M -- threshold to make a distinct cluster
%% enter $hs$, $hf$, $m$ if necessary
if ~exist('hs')
hs = input('please enter spatial bandwidth (hs):\n');
end
if ~exist('hf')
hf = input('please enter feature bandwidth (hf):\n');
end
if ~exist('m')
m = input('please enter minimum cluster size (m):\n');
end
switch upper(sMode)
case 'RGB'
RGB = double( RGB_raw );
case 'gray'
error('FCMcut must use colored image to do segmentation!')
end
sz = size(RGB);
mTCUT = Tcut( RGB(:,:,1) ); % trivial segmentation
%% project data into mean-shift space to make $MSSD$ (mean-shift space data)
mT = repmat([1:sz(1)]', 1, sz(2));
vX = mT(1:end)'; % row
mT = repmat([1:sz(2)], sz(1), 1);
vY = mT(1:end)'; % column
mT = RGB(:,:,1);
vR = mT(1:end)'; % red
mT = RGB(:,:,2);
vG = mT(1:end)'; % green
mT = RGB(:,:,3);
vB = mT(1:end)'; % blue
MSSD = [vX, vY, vR, vG, vB];
%% make $g$ - explicit profile function
disp('Using flat kernel: Epanechnikov kernel...')
g_s = ones(2*hs+1, 2); % 's' for support space
g_f = ones(2*hf+1, 3); % 'f' for feature space
%% main part $$
nIteration = 4;
nData = length(MSSD); % total number of data
DSD = MSSD*0; % 'DSD' for destination space data
for k = 1:nData
%
tMSSD = MSSD(k,:); % 't' for temp
for l = 1:nIteration
%
mT = abs( MSSD - repmat(tMSSD, nData, 1));
vT = logical( (mT(:,1)<=hs).*(mT(:,2)<=hs).*(mT(:,3)<=hf).*(mT(:,4)<=hf).*(mT(:,5)<=hf) );
v = MSSD(vT,:);
% update $tMSSD$
tMSSD = mean( v, 1 );
if nIteration == l
DSD(k,:) = tMSSD;
end
end
end
% show result
DRGB = RGB * 0;
DRGB(:,:,1) = reshape(DSD(:,3), sz(1), sz(2)); % red
DRGB(:,:,2) = reshape(DSD(:,4), sz(1), sz(2)); % red
DRGB(:,:,3) = reshape(DSD(:,5), sz(1), sz(2)); % red
figure, imshow(uint8(DRGB), [])

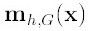 ,如果
,如果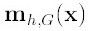 <ε(人工设定),推出程序。如果
<ε(人工设定),推出程序。如果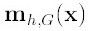 >ε, 则利用(3)计算x,返回1.
>ε, 则利用(3)计算x,返回1.![]() 代表空间位置的信息,离远点越近,其值就越大,
代表空间位置的信息,离远点越近,其值就越大,![]() 表示颜色信息,颜色越相似,其值越大。如图左上角图片,按照(4)计算的概率密度如图右上。利用meanshift对其聚类,可得到左下角的图。
表示颜色信息,颜色越相似,其值越大。如图左上角图片,按照(4)计算的概率密度如图右上。利用meanshift对其聚类,可得到左下角的图。















