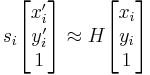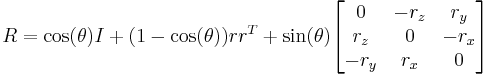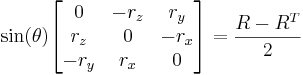OpenCV相机标定函数
原文转自:http://blog.sina.com.cn/s/blog_b364631a0101imw3.html
照相机定标
ProjectPoints2
投影三维点到图像平面
void cvProjectPoints2( const CvMat* object_points, const CvMat* rotation_vector, const CvMat* translation_vector, const CvMat* intrinsic_matrix, const CvMat* distortion_coeffs, CvMat* image_points, CvMat* dpdrot=NULL, CvMat* dpdt=NULL, CvMat* dpdf=NULL, CvMat* dpdc=NULL, CvMat* dpddist=NULL );
- object_points
- 物体点的坐标,为3xN或者Nx3的矩阵,这儿N是视图中的所有所有点的数目。
- rotation_vector
- 旋转向量,1x3或者3x1。
- translation_vector
- 平移向量,1x3或者3x1。
- intrinsic_matrix
-
摄像机内参数矩阵A:

- distortion_coeffs
- 形变参数向量,4x1或者1x4,为 [k1,k2,p1,p2]。如果是NULL,所有形变系数都设为0。
- image_points
- 输出数组,存储图像点坐标。大小为2xN或者Nx2,这儿N是视图中的所有点的数目。
- dpdrot
- 可选参数,关于旋转向量部分的图像上点的导数,Nx3矩阵。
- dpdt
- 可选参数,关于平移向量部分的图像上点的导数,Nx3矩阵。
- dpdf
- 可选参数,关于fx和fy的图像上点的导数,Nx2矩阵。
- dpdc
- 可选参数,关于cx和cy的图像上点的导数,Nx2矩阵。
- dpddist
- 可选参数,关于形变系数的图像上点的导数,Nx4矩阵。
函数cvProjectPoints2通过给定的内参数和外参数计算三维点投影到二维图像平面上的坐标。另外,这个函数可以计算关于投影参数的图像点偏导数的雅可比矩阵。雅可比矩阵可以用在cvCalibrateCamera2和cvFindExtrinsicCameraParams2函数的全局优化中。这个函数也可以用来计算内参数和外参数的反投影误差。 注意,将内参数和(或)外参数设置为特定值,这个函数可以用来计算外变换(或内变换)。
FindHomography
计算两个平面之间的透视变换
void cvFindHomography( const CvMat* src_points, const CvMat* dst_points, CvMat* homography );
- src_points
- 原始平面的点坐标,大小为2xN,Nx2,3xN或者 Nx3矩阵(后两个表示齐次坐标),这儿N表示点的数目。
- dst_points
- 目标平面的点坐标大小为2xN,Nx2,3xN或者 Nx3矩阵(后两个表示齐次坐标)。
- homography
- 输出的3x3的homography矩阵。
函数cvFindHomography计算源平面和目标平面之间的透视变换![]() .
.
使得反投影错误最小:
这个函数可以用来计算初始的内参数和外参数矩阵。由于Homography矩阵的尺度可变,所以它被规一化使得h33 = 1
CalibrateCamera2
利用定标来计算摄像机的内参数和外参数
void cvCalibrateCamera2( const CvMat* object_points, const CvMat* image_points, const CvMat* point_counts, CvSize image_size, CvMat* intrinsic_matrix, CvMat* distortion_coeffs, CvMat* rotation_vectors=NULL, CvMat* translation_vectors=NULL, int flags=0 );
- object_points
- 定标点的世界坐标,为3xN或者Nx3的矩阵,这里N是所有视图中点的总数。
- image_points
- 定标点的图像坐标,为2xN或者Nx2的矩阵,这里N是所有视图中点的总数。
- point_counts
- 向量,指定不同视图里点的数目,1xM或者Mx1向量,M是视图数目。
- image_size
- 图像大小,只用在初始化内参数时。
- intrinsic_matrix
-
输出内参矩阵(A)
 ,如果指定CV_CALIB_USE_INTRINSIC_GUESS和(或)CV_CALIB_FIX_ASPECT_RATION,fx、 fy、 cx和cy部分或者全部必须被初始化。
,如果指定CV_CALIB_USE_INTRINSIC_GUESS和(或)CV_CALIB_FIX_ASPECT_RATION,fx、 fy、 cx和cy部分或者全部必须被初始化。
- distortion_coeffs
- 输出大小为4x1或者1x4的向量,里面为形变参数[k1, k2, p1, p2]。
- rotation_vectors
- 输出大小为3xM或者Mx3的矩阵,里面为旋转向量(旋转矩阵的紧凑表示方式,具体参考函数cvRodrigues2)
- translation_vectors
- 输出大小为3xM或Mx3的矩阵,里面为平移向量。
- flags
-
不同的标志,可以是0,或者下面值的组合:
- CV_CALIB_USE_INTRINSIC_GUESS - 内参数矩阵包含fx,fy,cx和cy的初始值。否则,(cx, cy)被初始化到图像中心(这儿用到图像大小),焦距用最小平方差方式计算得到。注意,如果内部参数已知,没有必要使用这个函数,使用cvFindExtrinsicCameraParams2则可。
- CV_CALIB_FIX_PRINCIPAL_POINT - 主点在全局优化过程中不变,一直在中心位置或者在其他指定的位置(当CV_CALIB_USE_INTRINSIC_GUESS设置的时候)。
- CV_CALIB_FIX_ASPECT_RATIO - 优化过程中认为fx和fy中只有一个独立变量,保持比例fx/fy不变,fx/fy的值跟内参数矩阵初始化时的值一样。在这种情况下, (fx, fy)的实际初始值或者从输入内存矩阵中读取(当CV_CALIB_USE_INTRINSIC_GUESS被指定时),或者采用估计值(后者情况中fx和fy可能被设置为任意值,只有比值被使用)。
- CV_CALIB_ZERO_TANGENT_DIST – 切向形变参数(p1, p2)被设置为0,其值在优化过程中保持为0。
函数cvCalibrateCamera2从每个视图中估计相机的内参数和外参数。3维物体上的点和它们对应的在每个视图的2维投影必须被指定。这些可以通过使用一个已知几何形状且具有容易检测的特征点的物体来实现。这样的一个物体被称作定标设备或者定标模式,OpenCV有内建的把棋盘当作定标设备方法(参考cvFindChessboardCorners)。目前,传入初始化的内参数(当CV_CALIB_USE_INTRINSIC_GUESS不被设置时)只支持平面定标设备(物体点的Z坐标必须为全0或者全1)。不过3维定标设备依然可以用在提供初始内参数矩阵情况。在内参数和外参数矩阵的初始值都计算出之后,它们会被优化用来减小反投影误差(图像上的实际坐标跟cvProjectPoints2计算出的图像坐标的差的平方和)。
FindExtrinsicCameraParams2
计算指定视图的摄像机外参数
void cvFindExtrinsicCameraParams2( const CvMat* object_points, const CvMat* image_points, const CvMat* intrinsic_matrix, const CvMat* distortion_coeffs, CvMat* rotation_vector, CvMat* translation_vector );
- object_points
- 定标点的坐标,为3xN或者Nx3的矩阵,这里N是视图中的个数。
- image_points
- 定标点在图像内的坐标,为2xN或者Nx2的矩阵,这里N是视图中的个数。
- intrinsic_matrix
-
内参矩阵(A)
 。
。
- distortion_coeffs
- 大小为4x1或者1x4的向量,里面为形变参数 [k1,k2,p1,p2]。如果是NULL,所有的形变系数都为0。
- rotation_vector
- 输出大小为3x1或者1x3的矩阵,里面为旋转向量(旋转矩阵的紧凑表示方式,具体参考函数cvRodrigues2)。
- translation_vector
- 大小为3x1或1x3的矩阵,里面为平移向量。
函数cvFindExtrinsicCameraParams2使用已知的内参数和某个视图的外参数来估计相机的外参数。3维物体上的点坐标和相应的2维投影必须被指定。这个函数也可以用来最小化反投影误差。
Rodrigues2
进行旋转矩阵和旋转向量间的转换
int cvRodrigues2( const CvMat* src, CvMat* dst, CvMat* jacobian=0 );
- src
- 输入的旋转向量(3x1或者1x3)或者旋转矩阵(3x3)。
- dst
- 输出的旋转矩阵(3x3)或者旋转向量(3x1或者1x3)
- jacobian
- 可选的输出雅可比矩阵(3x9或者9x3),关于输入部分的输出数组的偏导数。
函数转换旋转向量到旋转矩阵,或者相反。旋转向量是旋转矩阵的紧凑表示形式。旋转向量的方向是旋转轴,向量的长度是围绕旋转轴的旋转角。旋转矩阵R,与其对应的旋转向量r,通过下面公式转换:
![]()
![]()
反变换也可以很容易的通过如下公式实现:
旋转向量是只有3个自由度的旋转矩阵一个方便的表示,这种表示方式被用在函数cvFindExtrinsicCameraParams2和cvCalibrateCamera2内部的全局最优化中。
Undistort2
校正图像因相机镜头引起的变形
void cvUndistort2( const CvArr* src, CvArr* dst, const CvMat* intrinsic_matrix, const CvMat* distortion_coeffs );
- src
- 原始图像(已经变形的图像)。只能变换32fC1的图像。
- dst
- 结果图像(已经校正的图像)。
- intrinsic_matrix
-
相机内参数矩阵,格式为
 。
。
- distortion_coeffs
- 四个变形系数组成的向量,大小为4x1或者1x4,格式为 [k1,k2,p1,p2]。
函数cvUndistort2对图像进行变换来抵消径向和切向镜头变形。相机参数和变形参数可以通过函数cvCalibrateCamera2取得。使用本节开始时提到的公式,对每个输出图像像素计算其在输入图像中的位置,然后输出图像的像素值通过双线性插值来计算。如果图像得分辨率跟定标时用得图像分辨率不一样,fx、fy、cx和cy需要相应调整,因为形变并没有变化。
InitUndistortMap
计算形变和非形变图像的对应(map)
void cvInitUndistortMap( const CvMat* intrinsic_matrix, const CvMat* distortion_coeffs, CvArr* mapx, CvArr* mapy );
- intrinsic_matrix
- 摄像机内参数矩阵(A) [fx 0 cx; 0 fy cy; 0 0 1].
- distortion_coeffs
- 形变系数向量[k1, k2, p1, p2],大小为4x1或者1x4。
- mapx
- x坐标的对应矩阵。
- mapy
- y坐标的对应矩阵。
函数cvInitUndistortMap预先计算非形变对应-正确图像的每个像素在形变图像里的坐标。这个对应可以传递给cvRemap函数(跟输入和输出图像一起)。
FindChessboardCorners
寻找棋盘图的内角点位置
int cvFindChessboardCorners( const void* image, CvSize pattern_size, CvPoint2D32f* corners, int* corner_count=NULL, int flags=CV_CALIB_CB_ADAPTIVE_THRESH );
- image
- 输入的棋盘图,必须是8位的灰度或者彩色图像。
- pattern_size
- 棋盘图中每行和每列角点的个数。
- corners
- 检测到的角点
- corner_count
- 输出,角点的个数。如果不是NULL,函数将检测到的角点的个数存储于此变量。
- flags
-
各种操作标志,可以是0或者下面值的组合:
- CV_CALIB_CB_ADAPTIVE_THRESH - 使用自适应阈值(通过平均图像亮度计算得到)将图像转换为黑白图,而不是一个固定的阈值。
- CV_CALIB_CB_NORMALIZE_IMAGE - 在利用固定阈值或者自适应的阈值进行二值化之前,先使用cvNormalizeHist来均衡化图像亮度。
- CV_CALIB_CB_FILTER_QUADS - 使用其他的准则(如轮廓面积,周长,方形形状)来去除在轮廓检测阶段检测到的错误方块。
函数cvFindChessboardCorners试图确定输入图像是否是棋盘模式,并确定角点的位置。如果所有角点都被检测到且它们都被以一定顺序排布(一行一行地,每行从左到右),函数返回非零值,否则在函数不能发现所有角点或者记录它们地情况下,函数返回0。例如一个正常地棋盘图右8x8个方块和7x7个内角点,内角点是黑色方块相互联通地位置。这个函数检测到地坐标只是一个大约地值,如果要精确地确定它们的位置,可以使用函数cvFindCornerSubPix。
DrawChessBoardCorners
绘制检测到的棋盘角点
void cvDrawChessboardCorners( CvArr* image, CvSize pattern_size, CvPoint2D32f* corners, int count, int pattern_was_found );
- image
- 结果图像,必须是8位彩色图像。
- pattern_size
- 每行和每列地内角点数目。
- corners
- 检测到地角点数组。
- count
- 角点数目。
- pattern_was_found
- 指示完整地棋盘被发现(≠0)还是没有发现(=0)。可以传输cvFindChessboardCorners函数的返回值。
当棋盘没有完全检测出时,函数cvDrawChessboardCorners以红色圆圈绘制检测到的棋盘角点;如果整个棋盘都检测到,则用直线连接所有的角点。
姿态估计
CreatePOSITObject
初始化包含对象信息的结构
CvPOSITObject* cvCreatePOSITObject( CvPoint3D32f* points, int point_count );
- points
- 指向三维对象模型的指针
- point_count
- 对象的点数
函数 cvCreatePOSITObject 为对象结构分配内存并计算对象的逆矩阵。
预处理的对象数据存储在结构CvPOSITObject中,只能在OpenCV内部被调用,即用户不能直接读写数据结构。用户只可以创建这个结构并将指针传递给函数。
对象是在某坐标系内的一系列点的集合,函数 cvPOSIT计算从照相机坐标系中心到目标点points[0] 之间的向量。
一旦完成对给定对象的所有操作,必须使用函数cvReleasePOSITObject释放内存。
POSIT
执行POSIT算法
void cvPOSIT( CvPOSITObject* posit_object, CvPoint2D32f* image_points, double focal_length, CvTermCriteria criteria, CvMatr32f rotation_matrix, CvVect32f translation_vector );
- posit_object
- 指向对象结构的指针
- image_points
- 指针,指向目标像素点在二维平面图上的投影。
- focal_length
- 使用的摄像机的焦距
- criteria
- POSIT迭代算法程序终止的条件
- rotation_matrix
- 旋转矩阵
- translation_vector
- 平移矩阵.
函数 cvPOSIT 执行POSIT算法。图像坐标在摄像机坐标系统中给出。焦距可以通过摄像机标定得到。算法每一次迭代都会重新计算在估计位置的透视投影。
两次投影之间的范式差值是对应点中的最大距离。如果差值过小,参数criteria.epsilon就会终止程序。
ReleasePOSITObject
释放3D对象结构
void cvReleasePOSITObject( CvPOSITObject** posit_object );
- posit_object
- 指向 CvPOSIT 结构指针的指针。
函数 cvReleasePOSITObject 释放函数 cvCreatePOSITObject分配的内存。
CalcImageHomography
计算长方形或椭圆形平面对象(例如胳膊)的Homography矩阵
void cvCalcImageHomography( float* line, CvPoint3D32f* center, float* intrinsic, float* homography );
- line
- 对象的主要轴方向,为向量(dx,dy,dz).
- center
- 对象坐标中心 ((cx,cy,cz)).
- intrinsic
- 摄像机内参数 (3x3 matrix).
- homography
- 输出的Homography矩阵(3x3).
函数 cvCalcImageHomography 为从图像平面到图像平面的初始图像变化(defined by 3D oblong object line)计算Homography矩阵。
对极几何(双视几何)
FindFundamentalMat
由两幅图像中对应点计算出基本矩阵
int cvFindFundamentalMat( const CvMat* points1, const CvMat* points2, CvMat* fundamental_matrix, int method=CV_FM_RANSAC, double param1=1., double param2=0.99, CvMat* status=NULL);
- points1
- 第一幅图像点的数组,大小为2xN/Nx2 或 3xN/Nx3 (N 点的个数),多通道的1xN或Nx1也可以。点坐标应该是浮点数(双精度或单精度)。:
- points2
- 第二副图像的点的数组,格式、大小与第一幅图像相同。
- fundamental_matrix
- 输出的基本矩阵。大小是 3x3 或者 9x3 ,(7-点法最多可返回三个矩阵).
- method
-
计算基本矩阵的方法
- CV_FM_7POINT – 7-点算法,点数目= 7
- CV_FM_8POINT – 8-点算法,点数目 >= 8
- CV_FM_RANSAC – RANSAC 算法,点数目 >= 8
- CV_FM_LMEDS - LMedS 算法,点数目 >= 8
- param1
- 这个参数只用于方法RANSAC 或 LMedS 。它是点到对极线的最大距离,超过这个值的点将被舍弃,不用于后面的计算。通常这个值的设定是0.5 or 1.0 。
- param2
- 这个参数只用于方法RANSAC 或 LMedS 。 它表示矩阵正确的可信度。例如可以被设为0.99 。
- status
- 具有N个元素的输出数组,在计算过程中没有被舍弃的点,元素被被置为1;否则置为0。这个数组只可以在方法RANSAC and LMedS 情况下使用;在其它方法的情况下,status一律被置为1。这个参数是可选参数。
对极几何可以用下面的等式描述:
![]()
其中 F 是基本矩阵,p1 和 p2 分别是两幅图上的对应点。
函数 FindFundamentalMat 利用上面列出的四种方法之一计算基本矩阵,并返回基本矩阵的值:没有找到矩阵,返回0,找到一个矩阵返回1,多个矩阵返回3。 计算出的基本矩阵可以传递给函数cvComputeCorrespondEpilines来计算指定点的对极线。
例子1:使用 RANSAC 算法估算基本矩阵。 int numPoints = 100; CvMat* points1; CvMat* points2; CvMat* status; CvMat* fundMatr; points1 = cvCreateMat(2,numPoints,CV_32F); points2 = cvCreateMat(2,numPoints,CV_32F); status = cvCreateMat(1,numPoints,CV_32F); fundMatr = cvCreateMat(3,3,CV_32F); int num = cvFindFundamentalMat(points1,points2,fundMatr,CV_FM_RANSAC,1.0,0.99,status); if( num == 1 ) printf("Fundamental matrix was found\n"); else printf("Fundamental matrix was not found\n"); 例子2:7点算法(3个矩阵)的情况。 CvMat* points1; CvMat* points2; CvMat* fundMatr; points1 = cvCreateMat(2,7,CV_32F); points2 = cvCreateMat(2,7,CV_32F); fundMatr = cvCreateMat(9,3,CV_32F); int num = cvFindFundamentalMat(points1,points2,fundMatr,CV_FM_7POINT,0,0,0); printf("Found %d matrixes\n",num);
ComputeCorrespondEpilines
为一幅图像中的点计算其在另一幅图像中对应的对极线。
void cvComputeCorrespondEpilines( const CvMat* points, int which_image, const CvMat* fundamental_matrix, CvMat* correspondent_lines);
- points
- 输入点,是2xN 或者 3xN 数组 (N为点的个数)
- which_image
- 包含点的图像指数(1 or 2)
- fundamental_matrix
- 基本矩阵
- correspondent_lines
- 计算对极点, 3xN数组
函数 ComputeCorrespondEpilines 根据外级线几何的基本方程计算每个输入点的对应外级线。如果点位于第一幅图像(which_image=1),对应的对极线可以如下计算 :
![]()
其中F是基本矩阵,p1 是第一幅图像中的点, l2 - 是与第二幅对应的对极线。如果点位于第二副图像中 which_image=2),计算如下:
![]()
其中p2 是第二幅图像中的点,l1 是对应于第一幅图像的对极线,每条对极线都可以用三个系数表示 a, b, c:
![]()
归一化后的对极线系数存储在correspondent_lines 中。
ConvertPointsHomogenious
Convert points to/from homogenious coordinates
void cvConvertPointsHomogenious( const CvMat* src, CvMat* dst );
- src
- The input point array, 2xN, Nx2, 3xN, Nx3, 4xN or Nx4 (where N is the number of points). Multi-channel 1xN or Nx1 array is also acceptable.
- dst
- The output point array, must contain the same number of points as the input; The dimensionality must be the same, 1 less or 1 more than the input, and also within 2..4.
The function cvConvertPointsHomogenious converts 2D or 3D points from/to homogenious coordinates, or simply copies or transposes the array. In case if the input array dimensionality is larger than the output, each point coordinates are divided by the last coordinate:
- (x,y[,z],w) -> (x',y'[,z'])
-
其中
- x' = x/w
- y' = y/w
- z' = z/w (if output is 3D)
If the output array dimensionality is larger, an extra 1 is appended to each point.
(x,y[,z]) -> (x,y[,z],1)
Otherwise, the input array is simply copied (with optional tranposition) to the output. Note that, because the function accepts a large variety of array layouts, it may report an error when input/output array dimensionality is ambiguous. It is always safe to use the function with number of points N>=5, or to use multi-channel Nx1 or 1xN arrays.