Java求出矩阵表示的有向图所有的强连通分支程序设计过程
一、 问题
对矩阵表示的有向图,求出其所有的强连通分支,并指出最大强连通分支。最大连通分支定义为包含结点数最多的连通分支。
二、题目分析与设计
1. 题目的需求。
设计出一个基于界面的求强连通分支的软件,能根据相应的按键构建邻接矩阵,并绘画出相应的有向图,同时快速计算出其所有的强连通分支,并指出最大强连通分支同时绘画出最大的强连通分支,该小软件可用于数据结构的深度搜索的演示,同时也结合更直观的和简便的操作,也可用离散数学的教学。
2. 功能模块如下:
j构建按钮矩阵来动态输入邻接矩阵:用panel画板和GridLayout布局类创建按钮矩阵,用于对有向图的输入,每个按钮对应相应的点点连通;
k创建文本输入框用于输入和输出数据:共利用了两个文本输入框,一个用于确定有向图的点数,用于绘制按钮矩阵的一个参数,另外一个用于输出文本,限制为非编辑状态;
l绘制有向图:利用正多边形的几何关系,利用数学公式:P(i) = (S*R*cos(i*a + os),S*R*sin(i*a + os))算出顶点的坐标,其中P(i)代表第i个顶点,a = π/顶点数量*2,os 为偏移弧度,可利用此参数实现旋转,R为多边形外圆的半径,另外,增加参数S以实现缩放,只需将R*S即可来确定每个点在窗口的坐标,再利用直线的点斜式,来旋转线段来绘制箭头;
m寻找强连通分支:利用深度优先算法来实现强连通分支的个数,并记录每个分支的标志,和包含结点个数,并将最大的强连通分支矩阵复制给强连通分支临时矩阵,用于绘制强连通分支;
n绘制最大强连通分支:在得到最大的强连通分支后,而且标记这些点,即可根据点和坐标的对应关系绘出最大强连通图;
3. 程序功能层次图和程序结构流程图:
4. 开发环境为Eclipse SDK Version: 3.7.1
关键代码:
代码1:
////根据文本输入的N值来确定按钮矩阵的维数,和确定各个点相应的代号和坐标,并调用Paint和Update和Original等函数来实现实时快速的画面转化和最大强连通图和有向图的显示
public voidtextValueChanged(TextEvent e)
{
//TODO Auto-generated method stub
if(txf1.getText().length()!=0)//判断有无整型字符输入
{
N = Integer.parseInt(txf1.getText().trim(),10);//字符转换
if(N<4)
return;
// System.out.printf("%d", N); //N=8;
Graphicsg=f.getGraphics();///获得Graphics类
MaxTree=newint[N][N];///用于保存有向图
Maxconnect=newint[N][N];///用于保存最大强连通矩阵
time1++;///用于刷新按钮矩阵
if(time1>1)
f.remove(pnl);
pnl=new Panel(new GridLayout(N,N));
pnl.setBounds(20,180,400,400);
button=new Button[N][N];
for (int i = 0; i <N; i++)
{
for (int j = 0; j <N; j++)
{
Stringstr=newString();
str=""+i+","+j;
button[i][j]=new Button(str);
pnl.add(button[i][j]);/////添加按钮矩阵
button[i][j].addActionListener(f);
}
}
f.add(pnl);
f.setVisible(true);
////初始化有向图
for (int i = 0; i <N; i++)
{
for (int j = 0; j <N; j++)
{
MaxTree[i][j] = 0;
}
}
int radius=80;
point=new Point[N];
pointBig=new Point[N];
Pointpointoringal=newPoint();
pointoringal.setLocation(width/3*2+80, 150);
character=newchar[N];
////标记相应的点,和利用正多边形的数学关系式确定坐标
for(int i=0;i<N;i++)
{// System.out.println(i);
character[i]=(char) ('a'+i);
point[i]=new Point();
pointBig[i]=new Point();
double xtemp=0;
double ytemp=0;
////////////////////////N>=3!!!!!!!!!!!!!!!!!!!!!!!!!!!!
xtemp=pointoringal.x+radius*Math.cos((i+1)*(Math.PI/N*2));
ytemp=pointoringal.y+radius*Math.sin((i+1)*(Math.PI/N*2));
point[i].setLocation(xtemp,ytemp);
xtemp=pointoringal.x+1.2*radius*Math.cos((i+1)*(Math.PI/N*2));
ytemp=pointoringal.y+1.2*radius*Math.sin((i+1)*(Math.PI/N*2));
pointBig[i].setLocation(xtemp,ytemp);
}
///更新窗口
update(g);
///画出有向图
original(g);
b=newint[N];
p=newint[N];
int MaxTreetemp[][]=newint[N][N];///用于防止逆向搜索时改变MaxTree[][];
for (int i = 0; i <N; i++)
{
for (int j = 0; j <N; j++)
{
MaxTreetemp[i][j]=MaxTree[i][j];
}
}
///调用深度优先算法搜索强连通分支
f.SCC(MaxTreetemp,character);
///绘制窗口
paint(g);
}
}
代码二:
/// 利用深度优先算法来实现强连通分支的个数,并记录每个分支的标志,和包含结点个数,并将最大的强连通分支矩阵复制给强连通分支临时矩阵,用于绘制强连通分支;
////深度优先算法
publicvoidDFS(intu,charcolor[],charfather[],intd[],intf[],intGt[][],charGn[])
{
color[u]='g';
time++;
d[u]=time;
b[bi]=u;
bi++;
int ul[];
ul=newint[N];
int L=ADJ(u,Gt,ul);
for(int i=0;i<L;i++)
{
if(color[ul[i]]=='w')
{
father[ul[i]]=Gn[u];
DFS(ul[i],color,father,d,f,Gt,Gn);////回归调用到下一个节点
}
}
color[u]='b';
time++;
f[u]=time;
p[pi]=u;
pi++;
}
//强连通分量
publicvoid SCC(int Gt[][],char Gn[])
{
char color[],father[];
color=newchar[N];
father=newchar[N];
int d[],f[];
d=newint[N];
f=newint[N];
//初始化
for(int i=0;i<N;i++)
{
d[i]=f[i]=-1;
father[i]='*';//////全部标记为正向不连通分支
color[i]='w';
}
time=bi=pi=0;
////正向搜索
for(int u=0;u<N;u++)
{
if(color[u]=='w')
DFS(u,color,father,d,f,Gt,Gn);/////正向连通分支搜索
}
time=bi=pi=0;//
Gtree(Gt);
int pp[];
pp=newint[N];
for(int c=0;c<N;c++)
{
color[c]='w';
d[c]=f[c]=-1;
father[c]='*';//////全部标记为逆向不连通分支
pp[c]=p[c];
}
///逆向搜索
for(int v=N-1;v>=0;v--)
{
if(color[pp[v]]=='w')
DFS(pp[v],color,father,d,f,Gt,Gn);/////逆向连通分支搜索
}
int t,r;
r=0;
//计算强连通分支的总个数和求出最大强连通分支
for(t=0;t<N;t++)
{
if(father[t]=='*')
{
r++;
}
}
Stringstr=newString();
str="强连通分支个数为:"+r;
txa1.setText(str);
////清空最大连通树Maxconnect
for (int i = 0; i <N; i++)
{
for (int j = 0; j <N; j++)
{
Maxconnect[i][j] = 0;
}
}
//////////////////画出连通分支(只画最大的)
int lastt=0;
int gap=0;
int maxt=0;
if(r!=N)
{
for(t=0;t<N;t++)
{
lastt=t;
if(father[b[t]]=='*')
{
for(r=t+1;r<N;r++)
{
if(father[b[r]]=='*')
{
t=r-1;
break;
}
}
if(gap<=(t+1-lastt))
{
gap=(t+1-lastt);
maxt=lastt;
}
}
}
//////////////////////////////找出最大连通树,并赋值给最大连通树Maxconnect
/////////////////////// (由于时间有限)算法较为粗糙,代码多
t=maxt;///用于定位最大分支起点
if(t!=N-1)
{////由标志逆置最大强连通分支
for(int i=0;i<N;i++)
{
if(character[i]==Gn[b[t]])
{
for (int j = 0; j <N; j++)
{
if(character[j]==Gn[b[t+1]])
{
Maxconnect[j][i] = 1;
break ;
}
}
}
}
}
else
{
for(int i=0;i<N;i++)
{////由标志逆置最大强连通分支
if(character[i]==Gn[b[t]])
{
for (int j = 0; j <N; j++)
{
if(character[j]==Gn[b[t+1]])
{
Maxconnect[j][i] = 1;
break ;
}
}
}
}
}
for(r=t+1;r<N;r++)
{////由标志逆置最大强连通分支
if(father[b[r]]!='*')
{
if(r!=N-1&&father[b[r+1]]!='*')
{/////////////////////////////////////////////////
for(int i=0;i<N;i++)
{
if(character[i]==Gn[b[r-1]])
{
for (int j = 0; j <N; j++)
{
if(character[j]==Gn[b[r]])
{
Maxconnect[j][i] = 1;
break ;
}
}
}
}
}
}
////得到Graphics类
Graphicsg=getGraphics();
////刷新窗口
update(g);
///绘制有向图
original(g);
////绘制最大强连通分支
MaxBranch(g);
}
5.不足,只能处理N>3的结点数的有向图;未能使用图像的双缓存技术来显示,所以屏幕有闪动的感觉;未能对非法操作做出反应。
三、测试分析
1. 典型测试数据:如图所示:
矩阵输入:
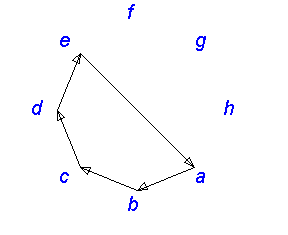
有向图:
测试数据的预计结果:如图所示:
2. 本程序的测试情况,与预计结果作对比
测试情况:如图所示:
结果与人工手算相同,而且用图像更直观的显示,让人一目了然。
3.结合界面和画图技术的直观结果更能让人容易观察结果,确实有效地减少了人工操作,还有按钮减少了手动输入的痛苦,更适合人性化。
代码和程序下载:http://download.csdn.net/detail/yanmy2012/4654437