R语言与回归分析学习笔记(应用回归小结)(1)
回归分析是计量与统计的一个核心话题。我的博客在这篇之前也写过两篇关于回归的文章:《R 语言与简单的回归分析》、《R语言与回归分析几个假设的检验》。后者很清楚的告诉了我们回归模型假设的严苛:响应变量不仅需要数值型的,而且还必须来自正态分布。但是在很多情况情况下他们是很难得到满足的:比如抽样调查时,我们经常只得到虚拟变量;再比如正态性的假设的同方差性极其难得。
我的博客之前贴出过回归分析的作业和我给的参考实现,今天这篇文章就是把应用回归分析作业中出现的一些命令,以及做作业时的一些感想贴出来与大家分享。
一些关于回归的理论知识可以通过查阅王松桂等编著的《线性统计模型》一书,我们在这里并不详述理论的推导。
一、回归的基础模型
回归模型的基本命令就是lm(),调用格式为:
lm(formula,data, subset, weights, na.action, method = "qr", model = TRUE, x =FALSE, y = FALSE, qr = TRUE, singular.ok = TRUE, contrasts = NULL, offset, ...)
这里method仅提供最小二乘法一种。Data必须为数据框。Formula可以是一元的,也可以是多元的,还可以有交互项,甚至可以没有常数项。我们以R中的数据集mtcars为例,说明回归模型。在R中敲入以下代码:
fit<-lm(mpg~hp+wt+hp:wt+I(wt^2),data=mtcars) summary(fit)
输出结果:
Call:
lm(formula= mpg ~ hp + wt + hp:wt + I(wt^2), data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.0714 -1.6122 -0.7299 1.3858 4.4947
Coefficients:
Estimate Std.Error t value Pr(>|t|)
(Intercept) 49.74766 3.69823 13.452 1.74e-13***
hp -0.12703 0.05770 -2.202 0.03643 *
wt -7.88960 2.77037 -2.848 0.00831**
I(wt^2) -0.09147 0.68536 -0.133 0.89482
hp:wt 0.02990 0.01714 1.745 0.09244.
---
Signif.codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05‘.’ 0.1 ‘ ’ 1
Residualstandard error: 2.192 on 27 degrees of freedom
MultipleR-squared: 0.8848, AdjustedR-squared: 0.8678
F-statistic:51.86 on 4 and 27 DF, p-value: 2.752e-12
从这个报告中,我们可以得到以下一些结论:
1、 我们设定的模型估计参数后的结果为:
mpg=49.75-0.13hp-7.89wt-0.09wt^2+0.03hp*wt
2、 我们可以知道交互效应是存在且明显的(统计意义上),wt的二次项作用不明显,模型可能需要去掉这一项。
3、 R^2=0.88,说明线性关系十分明显,整个模型在统计意义上也是有意义的(p-value: 2.752e-12)
综上,我们看出回归模型里可以包含数据项,数据项的变换(平方,根号,对数等),数据项的交互作用。这些都可以在formula里设置
二、回归诊断(例子摘自《R in action》)
为什么要做回归诊断?因为我们的回归报告中没有人告诉我们回归模型是否合适(也就是这个模型多大程度上满足guass-markov假定)我们以R中的states.x77为例来说明这个问题。
states<-as.data.frame(state.x77[,c("Murder","Population",
"Illiteracy","Income","Frost")])#简化数据框
cor(states)#相关性检测
library(car)
scatterplotMatrix(states,spread=F,lty.smooth=2)
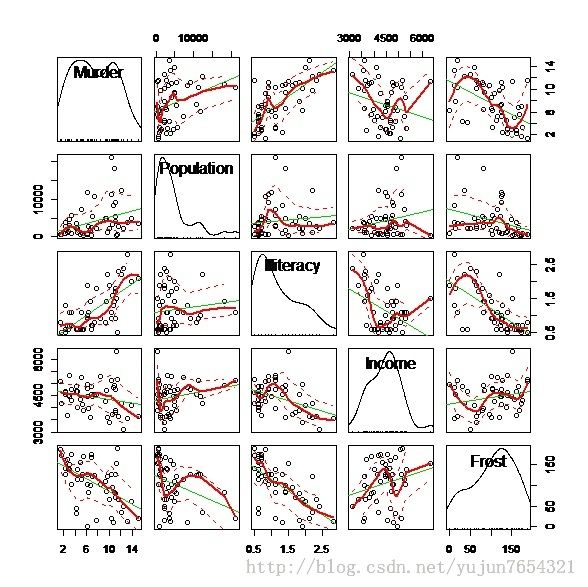
做出回归模型:
fit<-lm(Murder~.,data=states) summary(fit)#略去这部分输出结果
来看一下区间预测:
confint(fit)
2.5 % 97.5 %
(Intercept) -6.552191e+00 9.0213182149
Population 4.136397e-05 0.0004059867
Illiteracy 2.381799e+00 5.9038743192
Income -1.312611e-03 0.0014414600
Frost -1.966781e-02 0.0208304170
这里,我们看到frost包含0,也就是说,当其他条件不变时,谋杀率与温度改变无关。这是否符合预期?统计结果正确吗?我们不好回答,但肯定的是,数据满足统计假设的前提下,在统计意义上它很正确。
回归诊断技术为我们提供了评价回归模型适用性的必要工具。先看最简单与最直观的:
par(mfrow=c(2,2)) plot(fit)

从图中可以看到,除去Nevada一个异常点,模型还是拟合的很好的。通常在检验异方差性的时候,一个有用的建议就是做学生化残差图。我们试着做一下:
y.stu<-rstudent(fit) y.fit<-predict(fit) par(mfrow=c(2,1)) plot(y.stu~y.fit) hist(y.stu,freq=FALSE) lines(density(y.stu))

正如我们看到的,除了一个很明显的异常点,误差很好的服从了正态分布。至于独立性,同方差性,线性性(残差与拟合值无关)参见之前的博文《R语言与回归分析几个假设的检验》。
最后介绍线性模型的综合验证,使用gvlma包中的函数:gvlma()。其调用格式为:
gvlma(x,data, alphalevel = 0.05, timeseq, ...)
gvlma.form(formula,data, alphalevel = 0.05, timeseq = 1:nrow(data), ...)
gvlma.lm(lmobj, alphalevel = 0.05, timeseq)
在R中继续输入代码:
library(gvlma) gvlam(fit)
输出结果:
Call:
lm(formula= Murder ~ ., data = states)
Coefficients:
(Intercept) Population Illiteracy Income Frost
1.235e+00 2.237e-04 4.143e+00 6.442e-05 5.813e-04
ASSESSMENTOF THE LINEAR MODEL ASSUMPTIONS
USINGTHE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
Level ofSignificance = 0.05
Call:
gvlma(x = fit)
Value p-value Decision
GlobalStat 2.7728 0.5965 Assumptions acceptable.
Skewness 1.5374 0.2150 Assumptions acceptable.
Kurtosis 0.6376 0.4246 Assumptions acceptable.
LinkFunction 0.1154 0.7341 Assumptions acceptable.
Heteroscedasticity 0.4824 0.4873 Assumptions acceptable.
最后再提一下复共线性,所谓复共线性是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。一般来说,由于经济数据的限制使得模型设计不当,导致设计矩阵中解释变量间存在普遍的相关关系。(百度百科)
在R中判断多重共线性的命令为kappa(条件数),vif(膨胀因子)
我们继续上面的例子:
kappa(cor(states)) library(DAAG) vif(fit)
输出结果:
kappa(cor(states))
[1] 12.62042
vif(fit)
Population Illiteracy Income Frost
1.2453 2.1658 1.3458 2.0825
一般来说kappa大于1000,或vif大于10说明存在复共线性。
附注: R中的gvlma函数
function(x, data, alphalevel = 0.05, timeseq, ...)
{
mc <- match.call()
extras <- match.call(expand.dots =FALSE)$...
if (class(x) == "formula") {
if (missing(timeseq))
timeseq = 1:nrow(data)
calllist <- call(name ="gvlma.form", formula = x, data = as.name(deparse(substitute(data))),
alphalevel = alphalevel, timeseq =timeseq)
if (length(extras) > 0) {
calllist <- c(as.list(calllist),extras)
calllist <- as.call(calllist)
}
z<- eval(calllist, parent.frame())
}
else z <- gvlma.lm(x, alphalevel,timeseq)
z$GlobalTest$call <- mc
z
}
<environment: namespace:gvlma>