hdu 1392 Surround the Trees 凸包周长

Surround the Trees

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 9486    Accepted Submission(s): 3648

Problem Description

There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him? 
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.



There are no more than 100 trees.

 

Input

The input contains one or more data sets. At first line of each input data set is number of trees in this data set, it is followed by series of coordinates of the trees. Each coordinate is a positive integer pair, and each integer is less than 32767. Each pair is separated by blank.

Zero at line for number of trees terminates the input for your program.

 

Output

The minimal length of the rope. The precision should be 10^-2.

 

Sample Input

   
   
   
   

    
    
    
    9 
12 7 
24 9 
30 5 
41 9 
80 7 
50 87 
22 9 
45 1 
50 7 
0 
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    243.06
   
   
   
   
   
   
   
   


   
   
   
   

凸包算法解释摘自;http://www.cnblogs.com/jbelial/archive/2011/08/05/2128625.html

平面凸包 ：

 定义： 对一个简单多边形来说，如果给定其边界上或内部的任意两个点，连接这两个点的线段上的所有点都被包含在该多边形的边界上或内部的话，则该多边形为凸多边形 。

在解决平面凸包下面介绍了两种算法：

一、  Graham扫描法，运行时间为O(nlgn)。

二、  Jarvis步进法，运行时间为O(nh),h为凸包中的顶点数。

                                       

Graham扫描法

   基本思想：通过设置一个关于候选点的堆栈s来解决凸包问题。

   操作：输入集合Q中的每一个点都被压入栈一次，非CH（Q）(表示Q的凸包)中的顶点的点最终将被弹出堆栈，当算法终止时，堆栈S中仅包含CH(Q)中的顶点，其顺序为个各顶点在边界上出现的逆时针方向排列的顺序。

注：下列过程要求|Q|>=3，它调用函数TOP（S）返回处于堆栈S 顶部的点，并调用函数NEXT-TO –TOP（S）返回处于堆栈顶部下面的那个点。但不改变堆栈的结构。

GRAHAM-SCAN(Q)

1           设P0 是Q 中Y 坐标最小的点，如果有多个这样的点则取最左边的点作为P0；

2           设<P1,P2,……,Pm>是Q 中剩余的点，对其按逆时针方向相对P0 的极角进行排序，如果有数个点有相同的极角，则去掉其余的点，只留下一个与P0 距离最远的那个点；

3           PUSH(p0 , S)

4           PUSH(p1 , S)

5           PUSH(p3 , S)

6           for i ← 3 to m

7               do while 由点NEXT-TOP-TOP（S），TOP（S）和Pi 所形成的角形成一次非左转

8                   do POP(S)

9               PUSH(pi , S)

10        return S

 

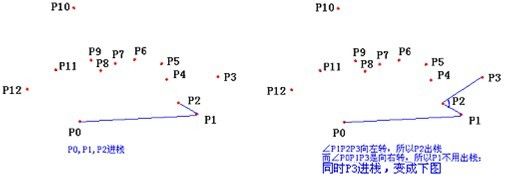
首先，找一个凸包上的点，把这个点放到第一个点的位置P0。然后把P1~Pm 按照P0Pi的方向排序，可以用矢量积(叉积)判定。

做好了预处理后开始对堆栈中的点<p3,p4,...,pm>中的每一个点进行迭代，在第7到8行的while循环把发现不是凸包中的顶点的点从堆栈中移去。（原理：沿逆时针方向通过凸包时，在每个顶点处应该向左转。因此，while循环每次发现在一个顶点处没有向左转时，就把该顶点从堆栈中弹出。）当算法向点pi推进、在已经弹出所有非左转的顶点后，就把pi压入堆栈中。

举例如下：

                            

                                  

                            

                                 

                                  

                                                         

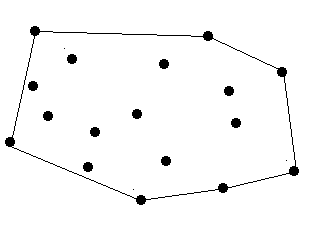
求这些点的凸包，然后凸包周长即为所求

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

int n;
const int maxn = 105;

struct Point {
	int x, y;
}p[maxn], stack[maxn];

int cross(Point a, Point b, Point c) {  //ab x ac
	return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}

double dis(Point a, Point b) {  //两点距离
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

bool cmp(const Point& a, const Point& b) {  //以p[0]为基准按照极角逆时针排序
	int t = cross(p[0], a, b);
	if (t < 0 || (t == 0 && dis(p[0], a) > dis(p[0], b)))
		return false;
	return true;
}

double Gram() {  //凸包Graham算法
	int mi = 0, x = p[0].x, y = p[0].y;
	for (int i = 1; i < n; i++) {  //找最坐下角的点
		if (p[i].x < x || (p[i].x == x && p[i].y < y)) {
			mi = i;
			x = p[i].x;
			y = p[i].y;
		}
	}
	Point tem = p[0];
	p[0] = p[mi];
	p[mi] = tem;

	sort(p + 1, p + n, cmp);  //逆时针排序

	p[n] = p[0];

	/*栈初始化，因为排序是逆时针，所以p[0]p[1] x p[0]p[2]
	 *一定大于等于零，stack[2]可以直接入栈
	*/
	stack[0] = p[0];
	stack[1] = p[1];
	stack[2] = p[2];

	int top = 2;

	for (int i = 3; i <= n; i++) {
		//若有右拐且栈内元素大于等于两个，弹出栈顶元素
		while (cross(stack[top - 1], stack[top], p[i]) <= 0 && top >= 2) --top;
		stack[++top] = p[i];
	}
	double ans = 0;
	for (int i = 0; i < top; i++) {
		ans += dis(stack[i], stack[i + 1]);
	}
	return ans;
}

int main()
{
	while (~scanf("%d", &n) && n) {
		for (int i = 0; i < n; i++) {
			scanf("%d%d", &p[i].x, &p[i].y);
		}
		if (n <= 1)
			puts("0.00");
		else if (n == 2)
			printf("%.2f\n", dis(p[0], p[1]));
		else {
			printf("%.2f\n", Gram());
		}
	}
	return 0;
}