R语言与抽样技术学习笔记(bootstrap)
R语言与抽样技术学习笔记(Randomize,Jackknife,bootstrap)
Bootstrap方法
Bootstrap一词来源于西方神话故事“The adventures of Baron Munchausen”归结出的短语“to pull oneself up by one's bootstrap",意味着不靠外界力量,依靠自身提升性能。
Bootstrap的基本思想是:因为观测样本包含了潜在样本的全部的信息,那么我们不妨就把这个样本看做“总体”。那么相关的统计工作(估计或者检验)的统计量的分布可以从“总体”中利用Monte Carlo模拟得到。其做法可以简单地概括为:既然样本是抽出来的,那我何不从样本中再抽样。
bootstrap基本方法
1、采用重抽样技术从原始样本中抽取一定数量(自己给定)的样本,此过程允许重复抽样。
2、根据抽出的样本计算给定的统计量T。
3、重复上述N次(一般大于1000),得到N个统计量T。其均值可以视作统计量T的估计。
4、计算上述N个统计量T的样本方差,得到统计量的方差。
上述的估计我们可以看成是Bootstrap的非参数估计形式,它基本的思想是用频率分布直方图来估计概率分布。当然Bootstrap也有参数形式,在已知分布下,我们可以先利用总体样本估计出对应参数,再利用估计出的分布做Monte Carlo模拟,得到统计量分布的推断。
值得一提的是,参数化的Bootstrap方法虽然不够稳健,但是对于不平滑的函数,参数方法往往要比非参数办法好,当然这是基于你对样本的分布有一个初步了解的基础上的。
例如:我们要考虑均匀分布\( U(\theta) \)的参数\( \theta \)的估计。我们采用似然估计。
data.sim <- runif(10) theta.hat <- max(data.sim) theta.boot1 <- replicate(1000, expr = { y <- sample(data.sim, size = 10, replace = TRUE) max(y) }) theta.boot1.estimate <- mean(theta.boot1) cat("the original estimate is ", theta.hat, "after bootstrap is ", theta.boot1.estimate)
## the original estimate is 0.7398 after bootstrap is 0.7138
hist(theta.boot1)
从结果来看,倒不是说估计有多不好,只是说方差比较大,而且它的经验分布真的不太像真正的分布,这个近似很糟糕,导致的直接结果是方差也很大。
如果采用参数方法,我们再来看看:
theta.boot2 <- replicate(1000, expr = { y <- runif(1000, 0, theta.hat) max(y) }) theta.boot2.estimate <- mean(theta.boot2) cat("the original estimate is ", theta.hat, "after bootstrap is ", theta.boot2.estimate)
## the original estimate is 0.7398 after bootstrap is 0.7391
hist(theta.boot2)
结果从直方图来看是更优秀了,估计也更好一些,关键是方差变小了,从非参数的0.0402减少到了7.3944 × 10-4。
bootstrap推断与bootstrap置信区间
既然我们已经得到了Bootstrap估计量的经验分布函数,那么一个自然的结果就是我们可以利用这个分布对统计量做出一些统计推断。例如可以推测估计量的方差,估计量的偏差,估计量的置信区间等。
现在,我们就来考虑如何做Bootstrap的统计推断。
利用Bootstrap估计偏差
既然Bootstrap将获得的样本样本看成了”总体“,那么估计量T自然是一个无偏的估计,Bootstrap数据集构造的”样本“的统计量T与原始估计量T的偏差自然就是估计量偏差的一个很好的估计。
具体做法是:
1. 从原始样本\( x_{1},\cdots,x_{n} \)中有放回的抽取n个样本构成一个Bootstrap数据集,重复这个过程m次,得到m个数据集。
2. 对于每个Bootstrap数据集,计算估计量T的值,记为\( T^{*j} \)。
3. \( T^{*j} \)的均值是T的无偏估计,而其与T的差是偏差的估计。
利用Bootstrap估计方差
估计量T的方差的估计可以看做每个Bootstrap数据集的统计量T的值的方差。
以我们遗留的问题,求1到100中随机抽取10个数的中位数的方差为例来说明。
n <- 10 x <- sample(1:100, size = n) Mboot <- replicate(1000, expr = { y <- sample(x, size = n, replace = TRUE) median(y) }) print(var(Mboot))
## [1] 334.2
这个应该是一个正确的估计了。Efron指出要得到标准差的估计并不需要非常多的Bootstrap数据集(m不需要过分的大),通常50已经不错了,m>200是比较少见的(区间估计可能需要多一些)
在R中,bootstrap包的函数bootstrap可以帮助你完成这一过程。bootstrap函数的调用格式如下:
bootstrap(x,nboot,theta,…, func=NULL)
参数说明:
- x:原始抽样数据
- theta:统计量T
- nboot:构造Bootstrap数据集个数
library(bootstrap) theta <- function(x) { median(x) } results <- bootstrap(x, 100, theta) print(var(results$thetastar))
## [1] 393.2
可以看到两个的结果是相近的,所以,利用这个函数还是不错的选择。类似的还有boot包的boot函数。我们在相关数据的Bootstrap推断中会用到。
相关数据的Bootstrap推断
回归数据的Bootstrap推断
我们之所以可以采用Bootstrap去做这些估计,蕴含了一个很重要的假设,这些样本是近似iid的,然而我们不能保证需要推断的数据都是近似独立同分布的,对于相关数据的Bootstrap推断,我们常用的方法有配对的Bootstrap(paired Bootstrap)与残差法。
先说paired Bootstrap,它的基本想法是,对于观测构成的数据框,虽然观测的每一行数据是相关的,但是每行是独立的,我们Bootstrap抽样,每次抽取一行,而不是单独的抽一个数即可。
例如,数据集women列出了美国女性的平均身高与体重,我们以体重为响应变量,身高为协变量进行回归,得到回归系数的估计。
使用paired Bootstrap:
m <- 200 n <- nrow(women) beta <- numeric(m) for (b in 1:m) { i <- sample(1:n, size = n, replace = TRUE) weight <- women$weight[i] height <- women$height[i] beta[b] <- lm(weight ~ height)$coef[2] } cat("the estimate of beta is", lm(weight ~ height, data = women)$coef[2], "paired bootstrap estimate is", mean(beta))
## the estimate of beta is 3.45 paired bootstrap estimate is 3.452
cat("the bias is", lm(weight ~ height, data = women)$coef[2] - mean(beta), "the stand error is", sd(beta))
## the bias is -0.002468 the stand error is 0.126
我们可以看到,估计量是无偏的,但是这个办法估计的方差变化较小,可能导致区间估计是不够稳健。我们可以利用boot包的boot函数来解决。
beta <- function(x, i) {
xi <- x[i, ]
coef(lm(xi[, 2] ~ xi[, 1]))[2]
}
library(boot)
obj <- boot(data = women, statistic = beta, R = 2000)
obj##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot(data = women, statistic = beta, R = 2000)
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* 3.45 -0.002534 0.1208
接下来我们说说残差法:
1. 由观测数据拟合模型.
2. 获得响应\( \hat{y}_{i} \)与残差\( \epsilon_{i} \)
3. 从残差数据集中有放回的抽取残差,构成Bootstrap残差数据集\( \hat{\epsilon}_{i} \)(这是近似独立的)
4. 构造伪响应\( Y_{i}^{*}=y_{i}+\hat{\epsilon}_{i} \)
5. 对x回归伪响应Y,得到希望得到的统计量,重复多次,得到希望的统计量的经验分布,利用它做统计推断
我们将women数据集的例子利用残差法在做一次,R代码如下:
lm.reg <- lm(weight ~ height, data = women) y.fit <- predict(lm.reg) y.res <- residuals(lm.reg) y.bootstrap <- rep(1, 15) beta <- NULL for (p in 1:100) { for (i in 1:15) { res <- sample(y.res, 1, replace = TRUE) y.bootstrap[i] <- y.fit[i] + res } beta[p] <- lm(y.bootstrap ~ women$height)$coef[2] } cat("the estimate of beta is", lm(weight ~ height, data = women)$coef[2], "paired bootstrap estimate is", mean(beta))
## the estimate of beta is 3.45 paired bootstrap estimate is 3.436
cat("the bias is", lm(weight ~ height, data = women)$coef[2] - mean(beta), "the stand error is", sd(beta))
## the bias is 0.01436 the stand error is 0.08561
可以看到,利用残差法得到的方差更为稳健,做出的估计也更为的合理。
这里需要指出一点,Bootstrap虽然可以处理相关数据,但是在变量筛选方面,其效果远不如Cross Validation准则好。
时间序列数据中的Bootstrap方法
还有一类数据的相关性是上述假定也不满足的,那就是时间序列数列。那么如何利用Bootstrap来推断时间序列呢?我们以1947年–1991年美国GNP季度增长率数据为例进行说明。这个数据来自《金融时间序列分析》一书,数据可以在这里下载。
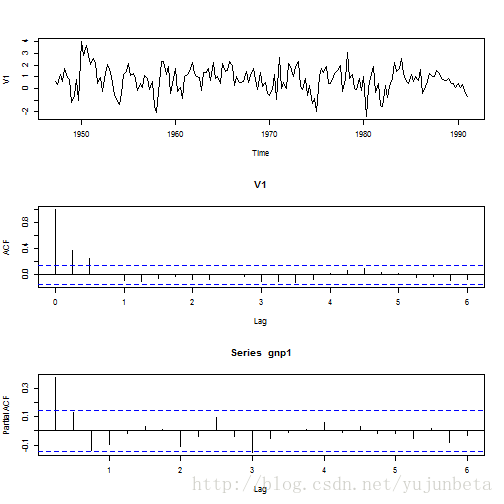
我们先来了解一下这个数据:
data <- read.table("D:/R/data/dgnp82.txt") gnp <- data * 100 gnp1 <- ts(gnp, fre = 4, start = c(1947, 2)) par(mfrow = c(3, 1)) plot(gnp1, type = "l") acf(gnp1, lag = 24) pacf(gnp1, lag = 24)
对于这个数据集,假设我想利用这些增长率估计平均增长率,显然直接从这些数据中有放回抽样是不合理的,因为它们是相依的,按照金融的说法,它们还存在波动性聚集。但是我们仍然不妨先这么计算,可以与之后的“正确”结果对比一下。
mean.boot <- replicate(1000, expr = { y <- sample(gnp1, size = 0.5 * length(gnp1), replace = TRUE) mean(y) }) cat("mean estimate is:", (mean.boot.estimate <- mean(mean.boot)), "variance is:", var(mean.boot))## mean estimate is: 0.7691 variance is: 0.01215对于这类问题,一个利用我们前面描述的办法可以解决的方案就是利用参数的Bootstrap方法。我们可以先考虑对时间序列建模:
library(tseries) adf.test(gnp1)## ## Augmented Dickey-Fuller Test ## ## data: gnp1 ## Dickey-Fuller = -5.153, Lag order = 5, p-value = 0.01 ## alternative hypothesis: stationary我们从上面的图片以及平稳性检验很快就可以发现,AR(3)是对这个时间序列的不错的描述,那么我们先求取这个模型的参数估计:
model <- arima(gnp1, order = c(3, 0, 0)) tsdiag(model)那么我们的参数Bootstrap可以这么做:
simu <- function(model) { n <- 1000 # Generate AR(3) process a <- as.numeric(coef(model)) e <- rnorm(n + 200, 0, sqrt(9.48e-05)) x <- double(n + 200) x[1:3] <- rnorm(3) for (i in 4:(n + 100)) { x[i] <- a[1] * x[i - 1] + a[2] * x[i - 2] + a[3] * x[i - 3] + a[4] + e[i] } x <- ts(x[-(1:200)]) mean(x) } mean.boot1 <- replicate(1000, expr = simu(model)) cat("mean estimate is:", (mean.boot.estimate <- mean(mean.boot)), "variance is:", var(mean.boot))## mean estimate is: 0.7691 variance is: 0.01215可以看到两者的结果是差不多的,究其原因是因为这是一个平稳过程,所以相差不大,我们来看一个非平稳的例子,很快就能发现不同:
data.sim <- arima.sim(list(order = c(2, 2, 0), ar = c(0.7, 0.2)), n = 500) cat("mean is:", mean(data.sim))## mean is: -5574## [1] "In the iid case:"mean.boot <- replicate(1000, expr = { y <- sample(data.sim, size = 2 * length(data.sim), replace = TRUE) mean(y) }) cat("mean estimate is:", (mean.boot.estimate <- mean(mean.boot)), "variance is:", var(mean.boot))## mean estimate is: -5560 variance is: 86089## [1] "In the dependence case:"model <- arima(data.sim, order = c(2, 2, 0)) simu <- function(model) { x <- arima.sim(list(order = c(2, 2, 0), ar = as.numeric(coef(model))), n = 500) mean(x) } mean.boot1 <- replicate(1000, expr = simu(model)) cat("mean estimate is:", (mean.boot.estimate <- mean(mean.boot)), "variance is:", var(mean.boot))## mean estimate is: -5560 variance is: 86089但是这种明显需要知道模型,或者正确模型设定才能得到比较好的结果的Bootstrap是不稳健的,如果上面我们采用了一个非真实的模型,结果会变为:
(model <- arima(data.sim, order = c(5, 3, 1)))## ## Call: ## arima(x = data.sim, order = c(5, 3, 1)) ## ## Coefficients: ## ar1 ar2 ar3 ar4 ar5 ma1 ## -1.149 -0.260 -0.137 -0.142 -0.024 0.897 ## s.e. 0.121 0.074 0.069 0.070 0.048 0.112 ## ## sigma^2 estimated as 1.02: log likelihood = -713.5, aic = 1441从建模的角度来说,这个也是不错的一个模型,那么它的估计可以由下面代码给出:
simu <- function(model) { x <- arima.sim(list(order = c(5, 3, 1), ar = as.numeric(coef(model))[1:5], ma = as.numeric(coef(model))[6]), n = 500, sd = sqrt(1.067)) mean(x) } mean.boot1 <- replicate(1000, expr = simu(model)) cat("mean estimate is:", (mean.boot.estimate <- mean(mean.boot)), "variance is:", var(mean.boot))## mean estimate is: -5560 variance is: 86089我们可以想见,在置信区间上这会给出一个比较宽的置信区间,这很有可能是我们不想见到的。那么,我们有没有稳健些的非参数方法呢?这是有的,这个方法通常被称为“Block Bootstrap”方法。
Block Bootstrap的思想很简单,虽然时间序列存在相关,但是自相关系数可能在若干延迟后就可以忽略不计了。那么我们取一个区间长度,将整个样本分为若干个区间,序列的顺序不改变,而区间之间看做近似独立的,我们对这些区间(block)做Bootstrap。如果区间间不存在重叠,我们称之为"Nonmoving block bootstrap";如果区间存在重叠(如样本为1, 2, 3, 4, 5, 6, 7, 8, 9, 10,我们将区间分为就可以称作"Moving block bootstrap"。
我们还是来考虑GNP数据,我们假设block长度为6,去掉前2个数据。利用"Nonmoving block bootstrap"我们有:data <- read.table("D:/R/data/dgnp82.txt") gnp <- data * 100 gnp <- gnp[-(1:2), 1] index <- matrix(1:174, 29, 6, byrow = TRUE) blocks <- NULL for (i in 1:29) { blocks <- rbind(blocks, gnp[index[i, ]]) } xbar <- NULL for (i in 1:10000) { take.blocks <- sample(1:29, 29, replace = T) newdat <- c(t(blocks[take.blocks, ])) xbar[i] <- mean(newdat) } hist(xbar)## the mean estimate is 0.7781 the sample standard deviation is 0.1016对于Moving block bootstrap,我们有:
data <- read.table("D:/R/data/dgnp82.txt") gnp <- data * 100 blocks <- gnp[1:6, 1] for (i in 2:(length(gnp[, 1]) - 5)) { blocks <- rbind(blocks, gnp[i:(i + 5), 1]) } # MOVING BLOCK BOOTSTRAP xbar <- NULL for (i in 1:10000) { take.blocks <- sample(1:(length(gnp[, 1]) - 5), 29, replace = TRUE) newdat = c(t(blocks[take.blocks, ])) xbar[i] = mean(newdat) } hist(xbar)## the mean estimate is 0.7896 the sample standard deviation is 0.1114在tseries包中提供了tsbootstrap函数,来完成block Bootstrap过程。函数调用格式如下:
tsbootstrap(x, nb = 1, statistic = NULL, m = 1, b = NULL, type = c(“stationary”,“block”), …)
参数说明:
- x:原始数据,必须是数值向量或时序列
- nb:Bootstrap数据集个数
- statistic:Bootstrap统计量
我们可以将上面的例子利用tsbootstrap函数再算一次:
data <- read.table("D:/R/data/dgnp82.txt") gnp <- data * 100 gnp1 <- ts(gnp, fre = 4, start = c(1947, 2)) tsbootstrap(gnp1, nb = 500, mean, type = "block")
##
## Call:
## tsbootstrap(x = gnp1, nb = 500, statistic = mean, type = "block")
##
## Resampled Statistic(s):
## original bias std. error
## 0.7741 0.0316 0.1056
这与我们算的也差不多。
最后,我们提一下自相关系数的Bootstrap估计,这个有些类似多元统计中用到的拉直变换的逆变换,我们仅通过tsbootstrap提供的example来看看,具体内容可以参阅Paolo Giudici et al.的*Computational Statistic*一书。
n <- 500 # Generate AR(1) process a <- 0.6 e <- rnorm(n + 100) x <- double(n + 100) x[1] <- rnorm(1) for (i in 2:(n + 100)) { x[i] <- a * x[i - 1] + e[i] } x <- ts(x[-(1:100)]) acflag1 <- function(x) { xo <- c(x[, 1], x[1, 2]) xm <- mean(xo) return(mean((x[, 1] - xm) * (x[, 2] - xm))/mean((xo - xm)^2)) } tsbootstrap(x, nb = 500, statistic = acflag1, m = 2)
##
## Call:
## tsbootstrap(x = x, nb = 500, statistic = acflag1, m = 2)
##
## Resampled Statistic(s):
## original bias std. error
## 0.61538 -0.00549 0.02701
Bootstrap置信区间
说到Bootstrap推断总会说到假设检验与置信区间。那么Bootstrap的置信区间如何求解呢?
一般来说有以下几种方法:
- 标准正态Bootstrap置信区间
- 基本Bootstrap置信区间
- 分位数Bootstrap置信区间
- Bootstrap t置信区间
- BCa 置信区间
先说说标准正态Bootstrap置信区间,这是通过构造伪Z统计量(\( z=\frac{\hat{\theta}-E(\hat{\theta})}{se(\hat{\theta})} \)),假设Z服从正态分布,根据Z的分位数来构造置信区间,当然假设Z服从t分布也是可以的。
基本的Bootstrap置信区间是由置信区间的定义\[ P ( L < \hat{\theta}-\theta < U )=1- \alpha \]得到的启发,利用Bootstrap分位数\( \hat{\theta}_{U}^{*} \)和\( \hat{\theta}_{L}^{*} \)来估计统计量的置信区间,即通过\[ P(\hat{\theta}_{L}^{*}-\hat{\theta}<\theta^{*}-\hat{\theta}<\hat{\theta}_{U}^{*}-\hat{\theta})\approx1-\alpha \]可以将区间估计为:\[ (2\hat{\theta} - \hat{\theta}_{U}^{*}\hspace{1em} ,\hspace{1em} 2\hat{\theta}-\hat{\theta}_{L}^{*}) \]
分位数Bootstrap的想法比较简单:既然我们将Bootstrap数据集求出的统计量的经验分布视为统计量的分布,那么它的置信区间自然就应该是这个统计量的上下两侧的分位数。
Bootstrap t置信区间又称为学生Bootstrap置信区间,它是通过Bootstrap构造伪t统计量(\( t=\frac{\hat{\theta}-E(\hat{\theta})}{se(\hat{\theta})} \)),这与正态Bootstrap置信区间类似,但是这与正态Bootstrap不同的是,统计量t并不是简单的服从student-t分布,而是构造Bootstrap数据集时,利用这个Bootstrap数据集再次进行Bootstrap,得到一个t统计量,由于我们有m个Bootstrap数据集,那么我们就有m个t统计量,利用这些t统计量的分位数作为t分布的分位数,求取置信区间。这里我们嵌套了一个Bootstrap是为了求出伪t统计量的方差,这在一些文献中又被称为经验Bootstrap
t置信区间。我们有时也会利用delta method 求解t统计量的方差,它的好处就在于不需要通过额外的Bootstrap求解方差了,时间上有优化,但是精度方面,究竟谁最优,还是有待商榷的。
BCa区间的想法是:分位数Bootstrap置信区间可能由于偏差或者偏度使得估计量没有那么好的覆盖率,我们声称的置信水平\( \alpha \)可能并不对应\( \alpha \)分位数,那么我就对估计量施加一个变换,使得它的偏差与偏度得到修正,那么就找到\( \alpha \)实际对应的分位数,利用实际的分位数给出估计。这是由Efron于1987年提出的,如果偏差与偏度都是0的话,它就是分位数法求出的置信区间了。偏差的修正是利用中位数的偏差来进行修正,偏度的修正是利用Jackknife估计得到的。
boot包里的boot.ci函数可以轻松地计算这5种置信区间,其调用格式为:
boot.ci(boot.out, conf = 0.95, type = “all”, index = 1:min(2,length(boot.out$t0)), var.t0 = NULL, var.t = NULL, t0 = NULL, t = NULL, L = NULL, h = function(t) t, hdot = function(t) rep(1,length(t)), hinv = function(t) t, …)
我们以computational statistics一书的Copper-Nickel Alloy数据为例说明这个函数的使用:
| ironcontent | corrosionloss |
|---|---|
| 0.01 | 127.6 |
| 0.48 | 124 |
| 0.71 | 110.8 |
| 0.95 | 103.9 |
| 1.19 | 101.5 |
| 0.01 | 130.1 |
| 0.48 | 122 |
| 1.44 | 92.3 |
| 0.71 | 113.1 |
| 1.96 | 83.7 |
| 0.01 | 128 |
| 1.44 | 91.4 |
| 1.96 | 86.2 |
这个数据是关于金属腐蚀与金属体积的数据,我们要估计的估计量为以腐蚀损失为响应变量的回归的自变量回归系数与截距项之比,(这里我们不考虑估计量的意义),这里我们可以利用delta方法,认为估计量就是两个回归系数的估计量之比。
theta.boot <- function(dat, ind) { y <- dat[ind, 1] z <- dat[ind, 2] theta <- as.numeric(coef(lm(z ~ y))[2]/coef(lm(z ~ y))[1]) model <- lm(z ~ y) cov.m <- summary(lm(z ~ y))$cov theta.var <- (theta^2) * (cov.m[2, 2]/(model$coef[2]^2) + cov.m[1, 1]/(model$coef[1]^2) - 2 * cov.m[1, 2]/(prod(model$coef))) theta.var <- as.numeric((theta.var)) c(theta, theta.var) } dat <- read.table("D:/R/data/alloy.txt", head = TRUE) boot.obj <- boot(dat, statistic = theta.boot, R = 2000) print(boot.obj)
##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot(data = dat, statistic = theta.boot, R = 2000)
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* -1.851e-01 -1.270e-03 8.342e-03
## t2* 7.466e-06 1.373e-06 3.244e-06
print(boot.ci(boot.obj))
## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 2000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = boot.obj)
##
## Intervals :
## Level Normal Basic Studentized
## 95% (-0.2002, -0.1675 ) (-0.1971, -0.1649 ) (-0.1978, -0.1690 )
##
## Level Percentile BCa
## 95% (-0.2053, -0.1730 ) (-0.2030, -0.1722 )
## Calculations and Intervals on Original Scale
这里的Bootstrap t利用的就是delta方法求解估计量\( \theta \)的方差的,与经验Bootstrap t有那么一点点的区别,我们这里也报告一个经验Bootstrap t的置信区间好了:
boot.t.ci <- function(x, B = 500, R = 100, level = 0.95, statistic) { # compute the bootstrap t CI x <- as.matrix(x) n <- nrow(x) stat <- numeric(B) se <- numeric(B) boot.se <- function(x, R, f) { # local function to compute the bootstrap estimate of standard error for # statistic f(x) x <- as.matrix(x) m <- nrow(x) th <- replicate(R, expr = { i <- sample(1:m, size = m, replace = TRUE) f(x[i, ]) }) return(sd(th)) } for (b in 1:B) { j <- sample(1:n, size = n, replace = TRUE) y <- x[j, ] stat[b] <- statistic(y) se[b] <- boot.se(y, R = R, f = statistic) } stat0 <- statistic(x) t.stats <- (stat - stat0)/se se0 <- sd(stat) alpha <- 1 - level Qt <- quantile(t.stats, c(alpha/2, 1 - alpha/2), type = 1) names(Qt) <- rev(names(Qt)) CI <- rev(stat0 - Qt * se0) } stat <- function(dat) { z <- dat[, 2] y <- dat[, 1] theta <- as.numeric(coef(lm(z ~ y))[2]/coef(lm(z ~ y))[1]) } ci <- boot.t.ci(dat, statistic = stat, B = 200, R = 50) print(ci)
## 2.5% 97.5%
## -0.2030 -0.1688
这个程序运行十分缓慢,我们看看他的运行时间:
system.time(boot.t.ci(dat, statistic = stat, B = 200, R = 50))
## user system elapsed
## 34.46 0.04 35.32
这对于我的落后的电脑来说是个很大的打击,估计要是不是R而是C++,matlab的话,可能会死掉吧。所以可以用delta method求解近似的估计问题,还是谨慎的使用经验Bootstrap t吧。还有这里都是使用paired Bootstrap给出的估计,你可以用残差法试试,看看估计区间会不会更大些。
Jackknife after bootstrap
我们前面介绍了利用Bootstrap估计给出偏差与方差的估计,而这些Bootstrap本身又是一个估计量,我们也想知道这个估计量的好坏,那么它们的偏差,方差怎么估计呢?再用一次Bootstrap,或者用一次Jackknife是一个不错的选择,但是这个效率是十分低下的,我们看经验Bootstrap就知道了,这是一个让人很厌烦的过程,在这里我们绝对不会再一次重复这个让人火大的操作。万幸的是,我们有一个稍微好些的办法来解决这个问题,这就是著名的Jackknife after Bootstrap。
我们将算法描述如下:
记\( X_{i}^{*} \)为一次Bootstrap抽样,\( X_{1}^{*},\cdots,X_{B}^{*} \)是样本大小为B的Bootstrap数据集,令\( J(i) \)表示不含总体样本的元素\( x_{i} \)的Bootstrap数据集,我们利用\( J(i) \)作为一次Jackknife重复,这有点类似delete-K Jackknife,标准差估计量的Jackknife估计为\[ \hat{se}_{jack}(\hat{se}_{Boot}(\hat{\theta}))=\sqrt{\frac{n-1}{n}\sum_{i=1}^{n}(\hat{se}_{Boot(i)}-\overline{\hat{se}_{Boot(\cdot)}})^2}\\\hat{se}_{Boot(i)}=\sqrt{\frac{1}{B(i)}\sum_{j\in
J(i)}(\hat{\theta}_{(j)}-\overline{\hat{\theta}_{(J(i))}})^2}\\\overline{\hat{\theta}_{(J(i))}}=\frac{1}{B(i)}\sum_{j\in J(i)}\hat{\theta}_{(j)} \]其中B(i)表示不含\( x_{i} \)的样本个数。
我们来看金属腐蚀与金属体积数据的估计量的方差的方差的估计:
dat <- read.table("D:/R/data/alloy.txt", head = TRUE) n <- nrow(dat) y <- dat[, 2] z <- dat[, 1] B <- 2000 theta.b <- numeric(B) # set up storage for the sampled indices indices <- matrix(0, nrow = B, ncol = n) # jackknife-after-bootstrap step 1: run the bootstrap for (b in 1:B) { i <- sample(1:n, size = n, replace = TRUE) y <- dat[i, 2] z <- dat[i, 1] theta.b[b] <- as.numeric(coef(lm(z ~ y))[2]/coef(lm(z ~ y))[1]) # save the indices for the jackknife indices[b, ] <- i } # jackknife-after-bootstrap to est. se(se) se.jack <- numeric(n) for (i in 1:n) { # in i-th replicate omit all samples with x[i] keep <- (1:B)[apply(indices, MARGIN = 1, FUN = function(k) { !any(k == i) })] se.jack[i] <- sd(theta.b[keep]) } print(sd(theta.b))## [1] 8.838e-05Bootstrap的方差缩减问题
要知道方差缩减,首先需要明白方差来源于何处?对于Bootstrap而言,方差的来源主要有两个方面:一个是原始样本抽样的方差,另一个是Bootstrap抽样产生的方差。
原始样本抽样的方差在这里我们假定是没法改进的,那么Bootstrap抽样的方差该如何减少呢?这可以借鉴Monte Carlo中的方差缩减技术,采用重要抽样,关联抽样等办法,其中关联抽样的方法运用于Bootstrap,就产生了平衡Bootstrap与方向Bootstrap两种方法。Further reading
看上去我们已经较为完善的讨论了随机化检验、Jackknife、Bootstrap的基本内容,但是我们还是有很多没涉及到的东西,特别是在时间序列的Bootstrap里关于block长度的确定,Bootstrap效率分析等。Shao和Tu(1995),Li和Maddala(1996)都较为详尽的讨论了Bootstrap在时间序列中的应用,后者还添加了不少Bootstrap在经济学中的应用。
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。