20150913K-means聚类.md
1.聚类的思想:
将一个有N个对象的数据集,构造成k(k<=n)个划分,每个划分代表一个簇。使得每个簇包含一个对象,每个对象有且仅属于一个簇。
对于给定的k,算法首先给出一个初始的划分方法,以后通过反复迭代的方法改变划分,使得每一次改进之后的划分方案都较前一次更好。
2.K-means聚类
2.1K-means聚类的思想
K-means算法使用广泛,有时候也作为其他聚类算法的基础。
算法首先随机选择k个对象,每个对象初始地代表了一个簇的平均值和中心。对剩余的每个对象根据其与各个簇中心的距离,将它赋给最近的簇。然后重新计算每个簇的平均值。这个过程不断重复,直到准则函数(常常使用最小平方误差)收敛。
其损失函数表达式为 ∑ki=1∑xj∈Sj(xj−μj)2
2.2K-means聚类的算法步骤
输入:n个样本数据,分别为$x_1,x_2,\cdots,x_n$
1. 随机选择k个聚类中心,$\mu_1,\mu_2,\cdots,\mu_k \in \mathbb{R}^{n}$
2. 针对剩余的样本数据,将其类别标签设为距离其最近的聚类中心的标签。
3. 将每个聚类中心的值更新为与该类所有样本的平均值。
4. 重复以上步骤,直到聚类中心的变化小于规定的阈值即可。2.3K-means聚类代码实现
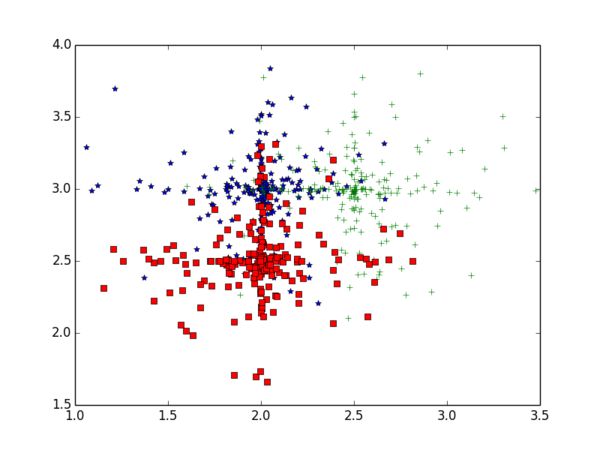
2.3.1随机构造二维数据集
# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
from numpy import *
import random
flag = ['b*','g+','rs','sb', 'db', '<b', 'pb']
def create():
num = 100
data = [[],[],[]]
dataCenter = [(2,3),(2.5,3),(2,2.5)]
for i in xrange(len(data)):
for j in xrange(num):
data[i].append((dataCenter[i][0]+random.uniform(-1,1)**2*random.uniform(-1,1), dataCenter[i][1]+random.uniform(-1,1)**2*random.uniform(-1,1)))
##draw picture
global flag
for i in xrange(len(data)):
for j in data[i]:
plt.plot(j[0],j[1],flag[i])
plt.show()
return data[0]+data[1]+data[2]2.3.2K-means聚类python实现
# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
from numpy import *
import random
##计算两个点之间的距离,这里采用的是欧式距离,关于距离的选择,看场景。
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA-vecB,2)))
##初始化选择k个质心,这里选用的是从n个点中随机选出k个质心。
def initCenter(data, k=2):
n = shape(data)[1]
centers = mat(zeros((k,n)))
for i in xrange(k):
index = int(random.uniform(0,len(data)))
centers[i] = data[index]
return centers
##计算上次和本次质心的距离偏差
def deltaCenter(centers, centersNext):
return sqrt(sum(power(centers-centersNext,2)))
def KMeans(data,k=2):
centers = initCenter(data, k)
centersNext = mat(zeros((k,shape(data)[1])))
dataNum = shape(data)[0]
clusterRes = mat(zeros((dataNum,2)))
eps = 0.01
delta = inf
freq = 10
while eps < delta and freq>0:
freq -= 1
##针对每个点划分类别
for i in xrange(dataNum):
mindist = inf
for j in xrange(k):
dist = distEclud(centers[j],data[i])
if dist<mindist:
mindist = dist
minIndex = j
clusterRes[i] = [minIndex,mindist]
##recalc the center of cluster
for j in xrange(k):
clusterData = data[nonzero(clusterRes[:,0].A==j)[0]]
centers[j] = mean(clusterData, axis=0)
##计算上一次聚类中心和这一次的变动
delta = deltaCenter(centers,centersNext)
##draw results
# global flag
# for i in xrange(k):
# clusterData = data[nonzero(clusterRes[:,0].A==i)[0]]
# for j in clusterData:
# plt.plot(j[0,0],j[0,1],flag[i])
# plt.show()
return centers,clusterRes
if __name__ == '__main__':
data = create()
KMeans(mat(data),3)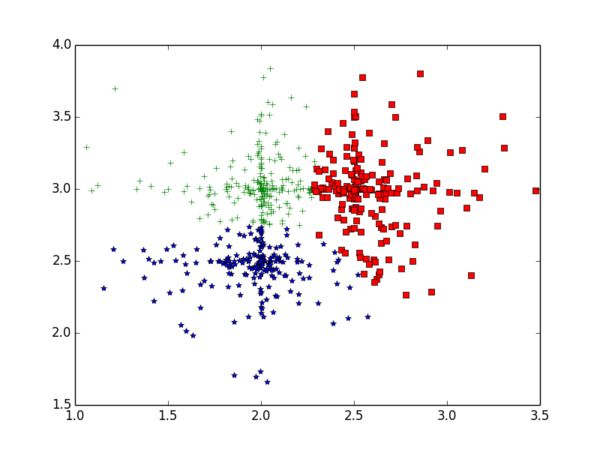
3个聚类中心依次为:[1.95408899 2.44211387] [ 1.97371672 3.04483904][ 2.59031316 2.9787235 ]
2.4K-means聚类缺点
初值敏感
对噪声敏感
不适于发现非凸面形状的簇或大小差别很大的簇
无法保证收敛到全局最优
有可能会出现某个聚类中心没有任何样本
3.二分K-means
3.1二分K-means算法步骤
由于K-means算法有时候容易收敛到局部最小值,因此就提出了二分K-means。
该算法是将所有点作为一个簇,然后将该簇一分为二,之后选择其中一个簇进行划分,选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE(误差平方和)的值,直到得到指定的簇数目为止。
聚类的SSE能够衡量聚类的性能,该值越小表示数据点越接近于它们的质心,聚类效果越好。所以
将所有数据看成一个簇,对该簇进行二分K-means
当簇的数目小于k时
对每一个簇
进行K-means划分,其中K=2
计算划分后的总误差
选择总误差最小的那个簇进行划分3.2二分K-means代码实现
# -*- coding:utf-8 -*-
########################################
# kmeans: k-means cluster
# Author : xuke
# Date : 2015-09-14
########################################
import matplotlib.pyplot as plt
from numpy import *
import random
flag = ['b*','g+','rs','sb', 'db', '<b', 'pb']
def biKmeans(data,k=2):
dataNum = shape(data)[0]
clusterRes = mat(zeros((dataNum,2)))
center0 = mean(data,axis=0).tolist()[0]
centers = [center0]
##计算一簇的簇心
for i in xrange(dataNum):
clusterRes[i,1] = distEclud(mat(center0), data[i])
while (len(centers) < k):
minSSE = inf
##遍历每个簇,划分每个簇,求得每个簇的SSE
for i in xrange(len(centers)):
dataNow = data[nonzero(clusterRes[:,0].A==i)[0],:]
centerTemp, clusterResTemp = KMeans(dataNow,2)
dataSSE = sum(clusterResTemp[:,1])
dataNoSSE = sum(clusterRes[nonzero(clusterRes[:,0].A!=i)[0],1])
if dataSSE + dataNoSSE < minSSE:
bestCluster = i
bestCenter = centerTemp
bestClusterResTemp = clusterResTemp.copy()
minSSE = dataSSE + dataNoSSE
##为选择出的最佳划分簇,打上类别,假设第2簇需要划分,且现在共有4簇,则第2簇打上2,4label。
bestClusterResTemp[nonzero(bestClusterResTemp[:,0].A == 1)[0],0] = len(centers)
bestClusterResTemp[nonzero(bestClusterResTemp[:,0].A == 0)[0],0] = bestCluster
##将最佳质心append进centers这个list
centers[bestCluster] = bestCenter[0,:].tolist()[0]
centers.append(bestCenter[1,:].tolist()[0])
clusterRes[nonzero(clusterRes[:,0].A == bestCluster)[0],:] = bestClusterResTemp
##draw results
global flag
for i in xrange(k):
clusterData = data[nonzero(clusterRes[:,0].A==i)[0]]
for j in clusterData:
plt.plot(j[0,0],j[0,1],flag[i])
plt.show()
return mat(centers), clusterRes
if __name__ == '__main__':
data = create()
# print KMeans(mat(data), 4)[0]
print biKmeans(mat(data), 3)[0]