POJ 1328-Radar Installation(贪心)
Radar Installation
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 71710 | Accepted: 16043 |
Description
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input is terminated by a line containing pair of zeros
Output
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
Source
题目意思:
在x轴上放雷达,它们能探测的范围都是半径为d的圆。再给定n个敌方位置,求至少放需要多少个雷达才能把这n个位置都覆盖探测到。
解题思路:
因为圆的方程 (x-a)²+(y-b)²=r²,所以任意一个敌方位置的左右区间范围:[x-sqrt(d*d-y*y),x+sqrt(d*d-y*y)]。
用结构体保存下每个敌方位置的左右区间l和r,再按l升序排列,然后从左往右依次取点,策略如下:
①首先将第一个位置点的右边作为第一个雷达的左边缘,判断②③;
②如果下一个位置的左边缘比当前雷达右边缘大,则需要一个新的雷达来覆盖,此时更新贪心的边缘为新位置的右边缘;
③如果下一个位置的右边缘比当前雷达右边缘小,则说明当前雷达可覆盖这个新的位置,此时更新贪心的边缘为新位置的右边缘;
n个位置都遍历完毕后输出雷达总数。
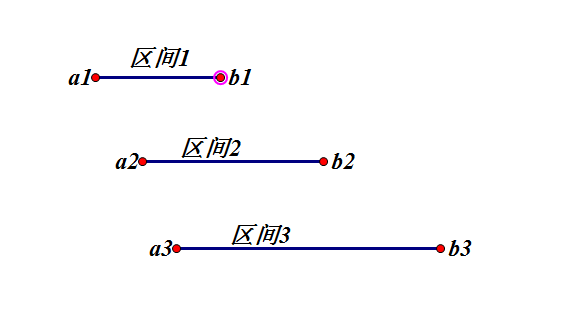
数轴上有n个闭区间[ai,bi]。取尽量少的点,使得每个区间内都至少有一个点(不同区间内含的点可以是同一个)。
贪心策略:
按照b1<=b2<=b3…(b相同时按a从大到小)的方式排序排序,从前向后遍历,当遇到没有加入集合的区间时,选取这个区间的右端点b。
证明:
为了方便起见,如果区间i内已经有一个点被取到,我们称区间i被满足。
1、首先考虑区间包含的情况,当小区间被满足时大区间一定被满足。所以我们应当优先选取小区间中的点,从而使大区间不用考虑。
按照上面的方式排序后,如果出现区间包含的情况,小区间一定在大区间前面。所以此情况下我们会优先选择小区间。
则此情况下,贪心策略是正确的。
2、排除情况1后,一定有a1<=a2<=a3……。
对于区间1来说,显然选择它的右端点是明智的。因为它比前面的点能覆盖更大的范围。
从而此情况下,贪心策略也是正确的。
坑爹啊啊啊啊啊!!排序用qsort一直WA,sort一下就A了!!心痛得无法呼吸。。
/*
* Copyright (c) 2016, 烟台大学计算机与控制工程学院
* All rights reserved.
* 文件名称:Radar Installation.cpp
* 作 者:单昕昕
* 完成日期:2016年4月27日
* 版 本 号:v1.0
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
struct Node
{
double l,r;
} N[1001];
/*int cmp(const void *a,const void *b)//qsort结构体排序
{
return (((Node*)a)->l<((Node*)b)->l);//升序排列
}*/
bool cmp(Node a,Node b)//sort结构体排序
{
return a.l < b.l;
}
int main()
{
double d;
int cnt=0,n;
while(cin>>n>>d&&(n||d))
{
int i,flag=0;
double x,y;
for(i=0; i<n; ++i)
{
cin>>x>>y;
if(y>d||d<0)
flag=1;
N[i].l=x-sqrt(d*d-y*y);
N[i].r=x+sqrt(d*d-y*y);
}
if(flag==1)
{
cout<<"Case "<<++cnt<<": "<<-1<<endl;
continue;
}
//qsort(N,n,sizeof(Node),cmp);//排序
sort(N,N+n,cmp);//排序
int ans=1;
double temp=N[0].r;
for(i=1; i<n; ++i)
{
if(N[i].l>temp)
{
temp=N[i].r;
++ans;
}
else if(N[i].r<=temp)
temp=N[i].r;
}
cout<<"Case "<<++cnt<<": "<<ans<<endl;
}
return 0;
}