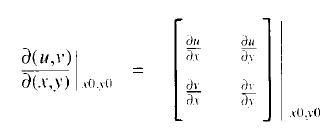流场（向量场）临界点的检测与分类

 

         帮实验室做流场的事情，因此临时在做毕设的同时穿插着看了几篇流场的论文。感慨就是英文太差、数学基础不够，C++不熟悉。总之，自己距离目标很遥远。今后努力的目标是，回顾高等代数、微分几何等知识。学习C++、OpenGl，MFC，STL。总之，很多要学习跟看的东西。需要加油的。

         然后记录一下看了几篇论文总结的临界点的检查与分类知识。

         定义1 　(临界点,Critical Points) :如果流场中某点P0 的三个速度分量均为零,而且存在一个包围P0 的邻域,该邻域内除P0 外任意点处的速度矢量均不为零,则P0 为该流场中的一个临界点,记为CP0 。

         首先是检测。现有的临界点检测方法包括MC 方法(Marching Cube ,MC)和基于几何代数的方法 。MC 方法是构造三维标量数据场中等值面的经典算法,把流场数据网格顶点的三个速度分量u （v ,w） 都分别当作标量来看待,就可以直接应用MC 方法得到v = 0 的点,但MC 方法只适合于六面体单元构成的规则而密集的数据场,不适用于稀疏的、不规则的数据场。Stephen Mann 等通过几何代数(Geometric Algebra) 的方法求出网格单元的poincare 指数ind ( c) ,如果ind ( c) ≠0 ,则该网格单元(cell) 必然存在临界点,这种

方法虽然可以准确地检测出临界点,但是算法难以理解而且计算量大。本文将Sperner 引理引入到临界点检测中,给出了临界点检测的新算法。

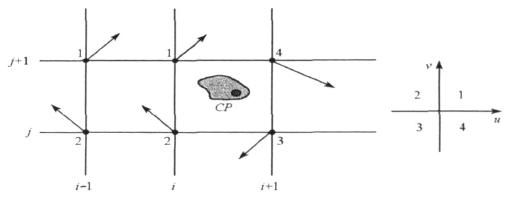
         根据定义可知，如果网格上的点是临界点，则可以很容易的判定，因为它的速度矢量均为0，下面讲解如果临界点不在网格边缘上而是在区域内如何判定。

简单理解就是看右图，向量的方向落在四个象限中分别给点标记成1、2、3、4.如果在一个区域内，如左图，即边界点包含1、2、3、4.则称为是Sperner 完全标号的，这样的区域内部必然包含至少一个临界点。

 

然后是将临界点分类。临界点分类是根据它的Jacobian矩阵的特征值决定的。首先来解释Jacobian矩阵。Jacobian矩阵是一个向量在另一个向量上的导数：

式子中的u,v是向量在x、y方向上的两个分量。这两个分量分别是用函数表示，分别是关于x、y的函数。因此，矩阵内部的值分别是u、v关于x、y的偏导数。

图中的R1、R2是Jacobian矩阵的特征值的实部，I1、I2是虚部。

如何计算特征值呢？

矩阵的特征值就是它的特征多项式的根。