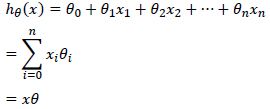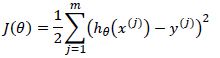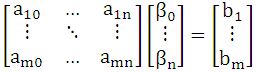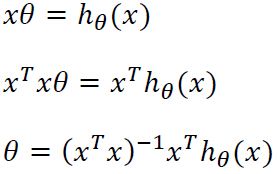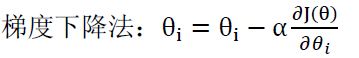【机器学习】机器学习(一、二):批梯度下降法、随机/增量梯度下降法、最小二乘法
前言:
STANFORD机器学习公开课第1、2课(Andrew Ng主讲),本文记录学习过程,整理学习笔记,并将MATLAB代码共享,以便回顾。
简介:
本节介绍机器学习中常用的线性回归模型,鉴于是第一节,为循序渐进的学习,本节中将分析一元线性回归。
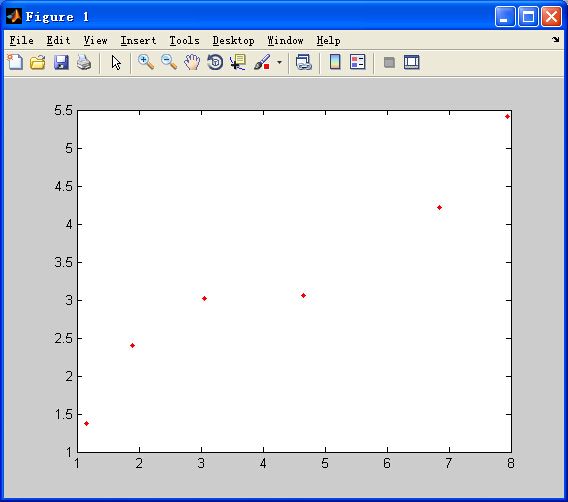
假设这里存在m组数据(x,y),其具体值如下(此处m=6):
| y | x |
| 1.37 | 1.15 |
| 2.4 | 1.9 |
| 3.02 | 3.06 |
| 3.06 | 4.66 |
| 4.22 | 6.84 |
| 5.42 | 7.95 |
从图上我们可以看出,大致数据的大致走势是可以用线性模型y=kx+b来表示的,为此我们建立一维线性回归模型。假设一维线性模型表达式如下,用n表示输入特征数,为方便计算,所有的样本都加入了x0=1这个特征,所以维数为n+1维。
式中:θ为待求解参数
误差函数如下表示,其中m为数据组数,即样本个数:
到此为止,前期工作做完。
现在要来求解θ的值,求解规则是:所有样本值的误差平方总和最小。在Andrew Ng的讲解中,有三种方法可以求得参数值:批梯度下降法、随机/增量梯度下降法、最小二乘法。
①最小二乘法
最小二乘法的严格推导就不推了,这里举一个通俗的例子,![]() 这是一个线性代数中常见的线性方程组,将其展开来看如下:
这是一个线性代数中常见的线性方程组,将其展开来看如下:
其中要求解的参数是β。若矩阵A是方阵,则![]() ;但是若A不是方阵,而是mx(n+1)的矩阵,则有如下做法:
;但是若A不是方阵,而是mx(n+1)的矩阵,则有如下做法:
这样就可以解除所有的参数了;由于一维线性回归同属于此类线性方程组问题,故同理可知:
由于最小二乘法的规则是求解最好的θ值,使误差平方和达到最小。在上式中,我们用y替换hθ (x),也就是说令hθ (x)=y,此时的误差肯定是最小的,说明此时的θ值是最好的。
故:
x矩阵,y矩阵如下,其中下标i表示第i个特征,上标j表示第j个样本:
根据以上分析,其MATLAB代码如下:
%最小二乘法线性拟合
clear all;
close all;
%%
%载入数据
load x.mat;
load y.mat;
%%
m=size(x,1);%样本数
n=size(x,2);%特征维数
theta=((x'*x)\x')*y;%参数拟合
figure;
plot(x(:,2),y,'r.');%原始数据
hold on;
y=theta'*x';%拟合数据
plot(x,y);
for i=1:n
fprintf('theta%d=%f;\n',i-1,theta(i,1));%打印估计的参数
end
%完
参数输出:
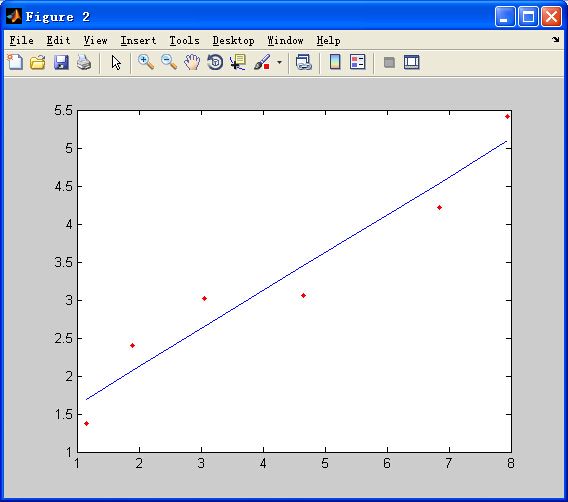
拟合效果(显然误差不为0,也就是说上面对最小二乘法的理解并不严格):
②批梯度下降法
式中α是学习速率,值太大可能导致不收敛;太小收敛得慢。正如上式,对等式右边第二项的求导过程如下:
由此可得(其中j为第j个样本):
根据上式,MATLAB代码如下:
%批梯度下降法
clc;
clear all;
close all;
load x.mat;
load y.mat;
n=size(x,2);%特征维数
m=size(x,1);%样本个数
alpha=0.001;
theta=zeros(n,1);%参数初始化为0向量
for k=1:10000
for j=1:m
for i=1:n
theta(i,1)=theta(i,1)-alpha*(x(j,:)*theta-y(j,1))*x(j,i);
end
end
end
figure;
plot(x(:,2),y,'r.');%原始数据
hold on;
y=theta'*x';%拟合数据
plot(x(:,2),y);
for i=1:n
fprintf('theta%d=%f;\n',i-1,theta(i,1));%打印估计的参数
end
%完
参数输出:
输出结果:
③随机/增量梯度下降法
在②中,讲解了批梯度下降法,代码中可以发现,每一个样本都要遍历所偶的特征,若样本个数m很大,特征n也很大(机器学习中很常见),那么批梯度下降法处理起来效率会较低。为此有一种改进的方法即随机/增量梯度下降法。
随机/增量梯度下降法的推导与上一模一样,只是在代码中做了改动。直接上MATLAB代码(注意理解同时更新theta值的含义):
%随机/增量度下降法
clear all;
close all;
load x.mat;
load y.mat;
figure;
plot(x(:,2),y,'r.');
n=size(x,2);%特征维数
m=size(x,1);%样本个数
alpha=0.01;%下降速度
theta=zeros(n,1);%参数
t=theta;
for iteration=1:1000%迭代次数
for i=1:n
t(i,1)=theta(i,1)-alpha*x(:,i)'*(x*theta-y);
end
theta=t;%同时更新theta值
end
figure;
plot(x(:,2),y,'r.');
hold on;
y=theta'*x';
plot(x(:,2),y);
for i=1:n
fprintf('theta%d=%f;\n',i-1,theta(i,1));%打印估计的参数
end
%完
输出参数:
输出结果:
小结:
到此,三个算法都讲解完毕,若有不妥和个人理解有误的地方,请大家多多指正。
本文所需要的实验数据及代码都已打包上传:http://download.csdn.net/detail/hujingshuang/8750323