2015年秋季腾讯校园招聘开发岗笔试题 四道大题之二

题目:2. 有下图的题解，请用 C/C++ 代码来列出满足下图 0-100 内的所有答案。

分析：用a1--a9表示九个数，其中a3=9，根据图中的信息，可以列出如下六个方程，

a1+a2-9=4       (1)

a4-a5*a6=4      (2)

a7+a8-a9=4      (3)

a1+a4/a7=4      (4)

a2-a5*a8=4       (5)

9-a6-a9=4         (6) 

6个方程8个未知数，自然解不出来的，所以如果在确定2个，则另外6个就可以算出来了，那么确定那两个呢？分析上面六个式子，由方程（4）则a1<=4范围一下缩小了很多

另外由(6)a6+a9=5,则a6<=5,a9<=5;那么a6是否是另一个要确定的数呢？假设是，我们继续往下算，这样0=<a1<=4,0=<a6<=5,a2、a9很容易的由a1、a6表示，但是求其他数

的时候，我发现有a4/a7,a5*a8两项，则其结果必然是两次方程，求解比较麻烦，所以a6不能是另一个要确定的数了。二次项产生的根源是a4/a7,a5*a8所以，所以避免求解二次方程

要确定a4、a5、a7、a8中的一个又（3）式a7+a8=4+a9<=9,则a7<=9,a8<=9;

所以取固定a1,a7;则分别求得各项如下：

a2=13-a1;

a4=(4-a1)*a7;

a8=(a2-4)*(9-a7)/(a2+a4-8);

a6=9-a7-a8;

a9=5-a6;

a5=(a2-4)/a8;

若求得的某一个值不在0-100的范围内，则此时的a1,a7不满足要求，这样只需两层循环即可；

两一个重要的问题是题中未说明a1-a9是整数，所以题目应该是有无数个解得；

设a1,a7未整数，则可以算得共有27组解，其中一组全部是整数。代码如下

#include<iostream>
#include<iomanip>

using namespace std;

#define IIO std::left<<setw(10)
#define II std::left<<setw(5)
float a1, a2, a3=9;
float a4, a5, a6;
float a7, a8, a9;

void f()
{
	int n = 0;
	for (int i = 0; i <= 4; i++){
		for (int j = 0; j <= 9; j++){
			a1 = (float)i/1.0;
			a7 = (float)j/1.0;

			a2 = 13 - a1;
			a4 = (4 - a1)*a7;

			a8 = (a2-4)*(9-a7) / (a2+a4-8);
			if (a8>100 || a8 < 0)
				continue;
			a6 = 9 - a7 - a8;
			if (a6>100 || a6 < 0)
				continue;
			a9 = 5 - a6;
			if (a9>100 || a9 < 0)
				continue;
			a5 = (a2 - 4) / a8;
			if (a5>100 || a5 < 0)
				continue;

			cout << II << a1 << IIO << a2 << IIO << a3 << " "<< a1 + a2 - a3 <<endl;
			cout << II << a4 << IIO << a5 << IIO << a6 << " "<< a4 - a5 * a6 <<endl;
			cout << II << a7 << IIO << a8 << IIO << a9 << " "<< a7 + a8 - a9 <<endl;
			cout << II << a1 + a4 / a7 << IIO << a2 - a5*a8 << IIO << a3 - a6 - a9 << endl;//验证
			cout << endl;
			n++;
		}
	}
	cout << n << endl;
}
int main()
{
	f();
	return 0;
}

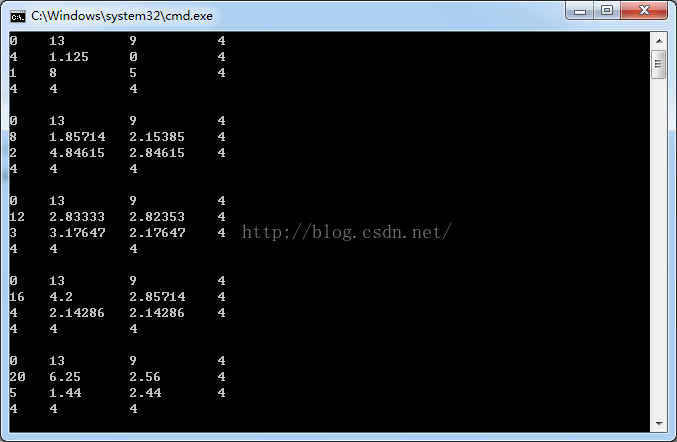
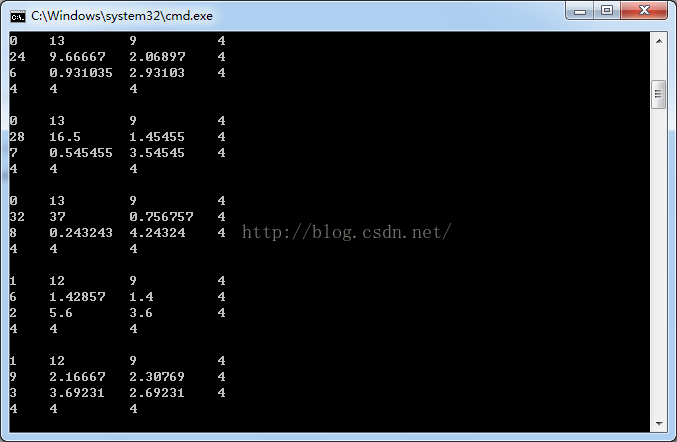
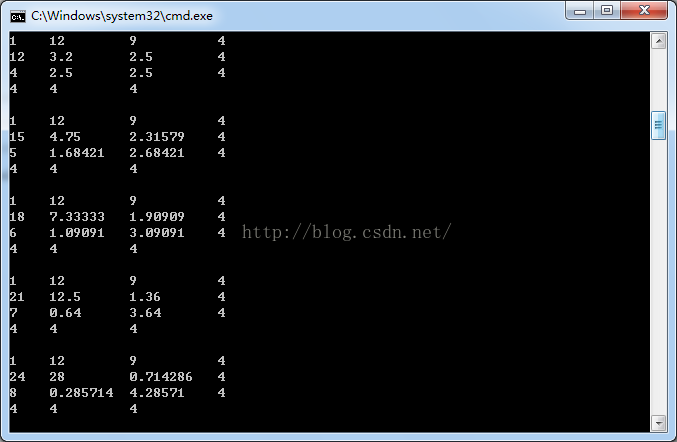
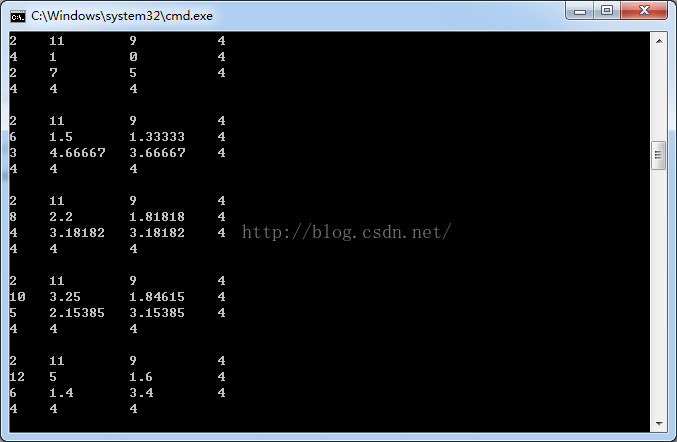
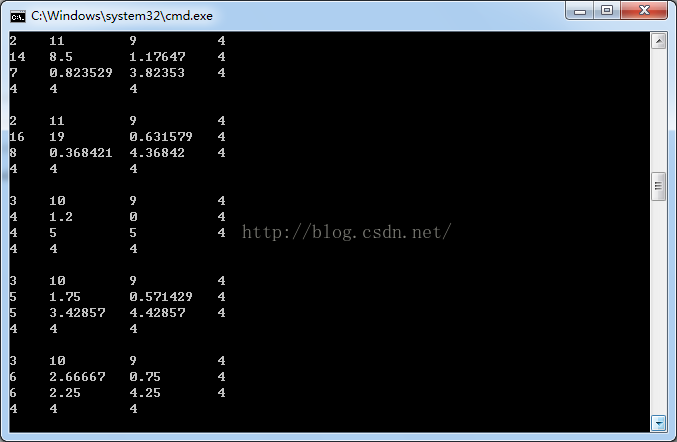
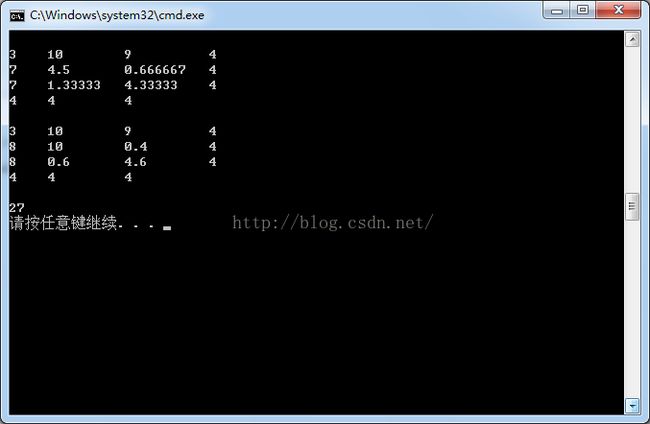
运行结果如下：27组

全部为整数结果为：

2      11      9

4      1        0

2      7        5

最多一位小数，5组；

继续下去，若a1,a7为最多一位小数点，运行得结果2283组

  若a1,a7为最多二位小数点，运行得结果224459组

  若a1,a7为最多三位小数点，运行得结果22410696组
  若a1,a7为最多四位小数点，运行得结果2240732806组

  。。。。。。

总结一下：若全部是整数则只有一组解

2      11      9

4      1        0

2      7        5

否则有无数组解；