HDU 3802 Ipad,IPhone
Ipad,IPhone
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 344 Accepted Submission(s): 126
Problem Description
In ACM_DIY, there is one master called “Lost”. As we know he is a “-2Dai”, which means he has a lot of money.

Well, Lost use Ipad and IPhone to reward the ones who solve the following problem.

In this problem, we define F( n ) as :

Then Lost denote a function G(a,b,n,p) as
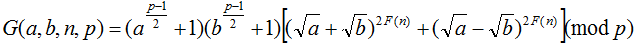
Here a, b, n, p are all positive integer!
If you could tell Lost the value of G(a,b,n,p) , then you will get one Ipad and one IPhone!

Well, Lost use Ipad and IPhone to reward the ones who solve the following problem.

In this problem, we define F( n ) as :

Then Lost denote a function G(a,b,n,p) as
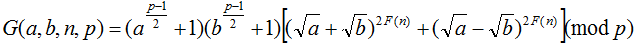
Here a, b, n, p are all positive integer!
If you could tell Lost the value of G(a,b,n,p) , then you will get one Ipad and one IPhone!
Input
The first line is one integer T indicates the number of the test cases. (T <= 100)
Then for every case, only one line containing 4 positive integers a, b, n and p.
(1 ≤a, b, n, p≤2*10 9 , p is an odd prime number and a,b < p.)
Then for every case, only one line containing 4 positive integers a, b, n and p.
(1 ≤a, b, n, p≤2*10 9 , p is an odd prime number and a,b < p.)
Output
Output one line,the value of the G(a,b,n,p) .
Sample Input
4 2 3 1 10007 2 3 2 10007 2 3 3 10007 2 3 4 10007
Sample Output
40 392 3880 9941
题意很简单:就是计算G(a,b,n,p);
分析:
数据很大
1.数学表达式中有斐波那契数列,但斐波那契数列定义域很大,所以用到了矩阵快速幂求解。
2.斐波那契数列解决后, 还有G表达式,G表达式可分成两部分,前半部分直接快速幂计算。
3.关键是后半部分,可以把他看成一个整体,求出数列特征方程,构建矩阵求解!
4.有一个比较难理解的地方时,取模问题:在求斐波那契数列时是对MOD-1取模,而在求其他数据时是对MOD取余,之所以这么做是因为求斐波那契数列时是对形如A^N取模,根据费马小定理,就是对MOD-1取模,而其他数据则不是A^N这种形式!(这里想了好久!)
细节部分:
关于取模问题,负数取模可以先让其加mod加到正数后再取模,也可以中间直接取模,最后在处理结果(取模)!
代码如下:
#include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;
ll mod;
struct Mar{
ll mat[2][2];
};
Mar E={1,0,0,1},unit2={0,1,1,1};
ll my_pow(ll a,ll b){
ll ans = 1;
while(b){
if (b%2)
ans = (ans*a)%mod;
b/=2;
a=(a*a)%mod;
}
return ans;
}
Mar mul(Mar a,Mar b){
ll fumod(ll);
Mar ans={0,0,0,0};
for (int i = 0; i < 2; ++i)
for (int j = 0; j < 2; ++j)
for (int k = 0; k <2; ++k){
ans.mat[i][j]+=(a.mat[i][k]*b.mat[k][j])%mod;
ans.mat[i][j]%=mod;
}
return ans;
}
Mar pow2(Mar a,ll n){
Mar ans = E;
while(n){
if (n%2)
ans = mul(ans,a);
n/=2;
a=mul(a,a);
}
return ans;
}
ll fib(ll n){
Mar uu={1,1,1,1};
Mar p=pow2(unit2,n);
p=mul(uu,p);
return p.mat[0][0];
}
int main()
{
ll T,a,b,n,p;
cin>>T;
while(T--){
cin >> a >> b >> n >> p;
mod = p;
ll temp1=(my_pow(a,(p-1)/2)+1)%mod;
ll temp2=(my_pow(b,(p-1)/2)+1)%mod;
if (!temp1 || !temp2){cout << "0" << endl;continue;}
--mod;
ll fn=fib(n);
++mod;
Mar unit={2,2*(a+b)%mod,1,1};
Mar tmp1={0,-(a-b)*(a-b)%mod,1,2*(a+b)%mod};
Mar p=pow2(tmp1,fn);
p=mul(unit,p);
ll pn=p.mat[0][0];
ll ans = pn%mod*temp1%mod*temp2%mod;
while(ans < 0)ans+=mod;
cout << ans << endl;
}
return 0;
}
