AC自动机（多模串匹配）

  首先简要介绍一下AC自动机：Aho-Corasick automation，该算法在1975年产生于贝尔实验室，是著名的多模匹配算法之一。一个常见的例子就是给出n个单词，再给出一段包含m个字符的文章，让你找出有多少个单词在文章里出现过。要搞懂AC自动机，先得有模式树（字典树）Trie和KMP模式匹配算法的基础知识。AC自动机算法分为3步：构造一棵Trie树，构造失败指针和模式匹配过程。
     如果你对KMP算法和了解的话，应该知道KMP算法中的next函数（shift函数或者fail函数）是干什么用的。KMP中我们用两个指针i和j分别表示，A[i-j+ 1..i]与B[1..j]完全相等。也就是说，i是不断增加的，随着i的增加j相应地变化，且j满足以A[i]结尾的长度为j的字符串正好匹配B串的前 j个字符，当A[i+1]≠B[j+1]，KMP的策略是调整j的位置（减小j值）使得A[i-j+1..i]与B[1..j]保持匹配且新的B[j+1]恰好与A[i+1]匹配，而next函数恰恰记录了这个j应该调整到的位置。同样AC自动机的失败指针具有同样的功能，也就是说当我们的模式串在Tire上进行匹配时，如果与当前节点的关键字不能继续匹配的时候，就应该去当前节点的失败指针所指向的节点继续进行匹配。
      看下面这个例子：给定5个单词：say she shr he her，然后给定一个字符串yasherhs。问一共有多少单词在这个字符串中出现过。我们先规定一下AC自动机所需要的一些数据结构，方便接下去的编程。

const int kind = 26; //26个小写字母
const int maxn = 500001; 
struct node
{
    node *fail; //失败指针
    node *next[kind];   //Trie树的next数组
    int count;   //是否为这个单词的最后一个结点
    node()
    {
        fail = NULL;
        count = 0;
        memset(next,NULL,sizeof(next));
    }
}; 
char keyword[51];//输入的单词
char str[1000001];//输入的文章
node *root;  //字典树的根节点
queue<node *> q; //在构造fail指针时bfs用的队列

 

有了这些数据结构之后，就可以开始编程了：
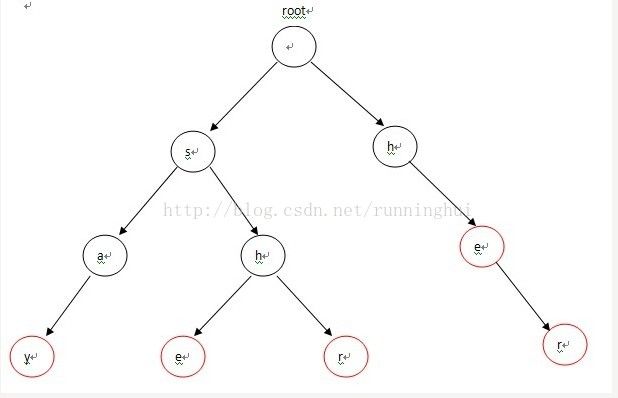
    首先，将这5个单词构造成一棵Tire，如图-1所示。

void insert(char *str,node *root) //构造Trie树
{
    node *p = root;
    int i=0,index;
    while(str[i])
    {
        index = str[i]-'a';
        if(p->next[index]==NULL)
        {
            p->next[index] = new node();
        }
        p = p->next[index];
        i++;
    }
    p->count++; //输入的这个单词的个数加1
}

 

在构造完这棵Tire之后，接下去的工作就是构造下失败指针。构造失败指针的过程概括起来就一句话：设这个节点上的字母为C，沿着他父亲的失败指针走，直到走到一个节点，他的儿子中也有字母为C的节点。然后把当前节点的失败指针指向那个字母也为C的儿子。如果一直走到了root都没找到，那就把失败指针指向root。具体操作起来只需要：先把root加入队列(root的失败指针指向自己或者NULL)，这以后我们每处理一个点，就把它的所有儿子加入队列，队列为空。

void build_ac_automation(node *root)//构造ac自动机的fail指针
{
    int i;
    root->fail = NULL;
    q.push(root);
    while(!q.empty())
    {
        node *tem  = q.front();
        q.pop();
        node *p = NULL;
        for(int i=0;i<kind;i++)
        {
            if(tem->next[i]!=NULL)
            {
                if(tem==root) tem->next[i]->fail = root;
                else
                {
                    p = tem->fail;
                    while(p!=NULL)
                    {
                        if(p->next[i]!=NULL)
                        {
                           tem->next[i]->fail = p->next[i];
                            break;
                        }
                        p = p->fail;
                    }
                    if(p==NULL) tem->next[i]->fail = root;
                }
                q.push(tem->next[i]);
            }
        }
    }
}

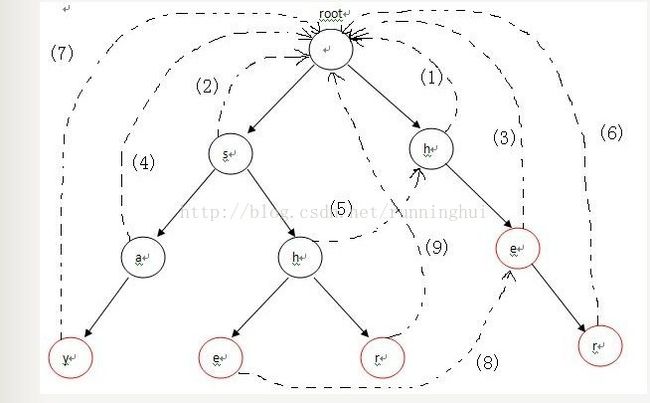
从代码观察下构造失败指针的流程：对照图-2来看，首先root的fail指针指向NULL，然后root入队，进入循环。第1次循环的时候，我们需要处理2个节点：root->next[‘h’-‘a’](节点h) 和 root->next[‘s’-‘a’](节点s)。把这2个节点的失败指针指向root，并且先后进入队列，失败指针的指向对应图-2中的(1)，(2)两条虚线；第2次进入循环后，从队列中先弹出h，接下来p指向h节点的fail指针指向的节点，也就是root；进入第13行的循环后，p=p->fail也就是p=NULL，这时退出循环，并把节点e的fail指针指向root，对应图-2中的(3)，然后节点e进入队列；第3次循环时，弹出的第一个节点a的操作与上一步操作的节点e相同，把a的fail指针指向root，对应图-2中的(4)，并入队；第4次进入循环时，弹出节点h(图中左边那个)，这时操作略有不同。在程序运行到14行时，由于p->next[i]!=NULL(root有h这个儿子节点，图中右边那个)，这样便把左边那个h节点的失败指针指向右边那个root的儿子节点h，对应图-2中的(5)，然后h入队。以此类推：在循环结束后，所有的失败指针就是图-2中的这种形式。

最后，我们便可以在AC自动机上查找模式串中出现过哪些单词了。匹配过程分两种情况：(1)当前字符匹配，表示从当前节点沿着树边有一条路径可以到达目标字符，此时只需沿该路径走向下一个节点继续匹配即可，目标字符串指针移向下个字符继续匹配；(2)当前字符不匹配，则去当前节点失败指针所指向的字符继续匹配，匹配过程随着指针指向root结束。重复这2个过程中的任意一个，直到模式串走到结尾为止。

int query(node *root) //字符串匹配
{
    int i=0,cnt=0,index,len = strlen(str);
    node *p = root;
    while(str[i])
    {
        index = str[i]-'a';
        while(p->next[index]==NULL&&p!=root)
            p = p->fail;
        p = p->next[index];
        p = (p==NULL)?root:p;
        node *tem = p;
        while(tem!=root&&tem->count!=-1)
        {
            cnt+=tem->count;
            tem->count = -1;//防止重新计数
            tem = tem->fail;
        }
        i++;
    }
    return cnt;
}

对照图-2，看一下模式匹配这个详细的流程，其中模式串为yasherhs。对于i=0,1。Trie中没有对应的路径，故不做任何操作；i=2,3,4时，指针p走到左下节点e。因为节点e的count信息为1，所以cnt+1，并且讲节点e的count值设置为-1，表示改单词已经出现过了，防止重复计数，最后temp指向e节点的失败指针所指向的节点继续查找，以此类推，最后temp指向root，退出while循环，这个过程中count增加了2。表示找到了2个单词she和he。当i=5时，程序进入第5行，p指向其失败指针的节点，也就是右边那个e节点，随后在第6行指向r节点，r节点的count值为1，从而count+1，循环直到temp指向root为止。最后i=6,7时，找不到任何匹配，匹配过程结束。
    到此为止AC自动机算法的详细过程已经全部介绍结束，看一道例题：http://acm.hdu.edu.cn/showproblem.php?pid=2222

如果完全理解了这个算法。这个题目用上面的模板即可解答。