最小生成树的边为主算法kruskal 九度acm1347: 孤岛连通工程
最小生成树的边为主算法kruskal模板(并查集):
主要思想:把边排序,从所有的边中逐个找最小的边进行连通判断及连接处理。
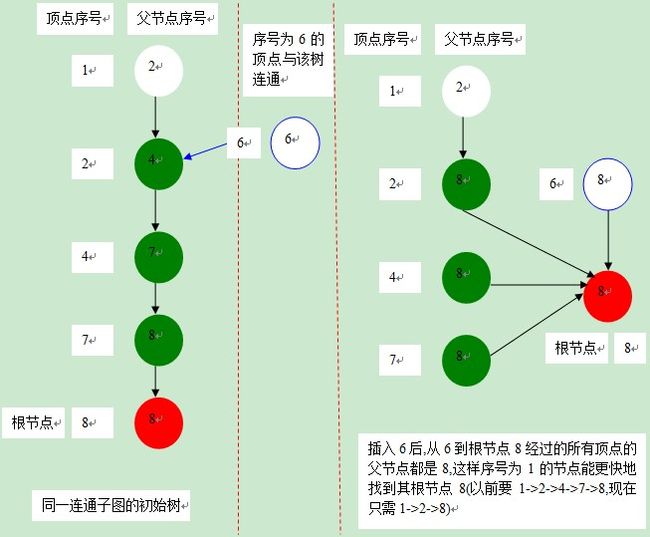
并查集的路径压缩如下(参考资料http://www.cnblogs.com/Veegin/archive/2011/04/29/2032423.html该网页的<并查集的路径压缩>图中,黑色为根节点,从下往上找到根节点):
上图中顶点序号1->2->4->7->8是有可能出现的,例如初始时,边1->2最短,则将1->2连通;然后,边2->4最短,则1->2->4连通;然后,边4->7最短,则1->2->4->7连通;最后,边7->8最短,则1->2->4->7->8连通。
下面代码中的MergeConnectedCom(a,b),当判断2个顶点(a、b)是否已经连通时,先找a、b的根结点(分别为a1、b1),如果a、b的根结点相同(即a1=b1),则表明a、b已经连通,无需再添加边将a、b连通了;否则将a的根结点a1的下一个指向b1,表明将a、b连通,成为同一类。
find(x)是查找某个顶点的根结点,并且对路径进行压缩,即访问某个结点a的根节点a1时,对从a到a1的路径上的所有点v,均指向a1,如上图中右边所示,这样每个点v到其根节点a1的路径更短,下次查找时能更快到达根结点a1,这样可以提高查找效率。
――――――
参考代码如下:
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <vector>
using namespace std;
const int MAX_NUM_VERTICES= 10001;//最大的节点个数
typedef struct Edge
{
int iIndexStart, iIndexEnd;//边的起点、终点节点的索引
int iWeight;//边的权值
}s_Edge;//图的边
//按边的权值从小到大对图的边向量排序(return < 则从小到大)
bool SortGraphEdgesByWeightAsc( const s_Edge& a, const s_Edge& b)
{
return a.iWeight< b.iWeight;
}
/*查找当前节点所在的连通分量的根节点,并逐一更新,将遍历到的节点的父节点都指向根节点,以便下次更快地查找
return: 父节点的索引,因为是递归,所以最终全都是根节点的索引*/
int find(int x)
{
if ( p[ x]!= x)//初值默认p[ x]=x,表明每个点都是孤立的,没有连通的.以后如果有子树,则子树节点的p[ x]不等于x,而等于其根节点y.
{
p[ x]= find( p[ x]);
}
return p[ x];//最终全都是根节点的索引
}
/*将2个连通分量合并(如果它们是连通的,则返回false,否则将它们合并成一个,并返回true)
参数: a:边的起点的下标索引
b:边的终点的下标索引
return: 如果起点所在的连通分量与起点所在的连通分量是同一个,则表明它们已经连通了,无需再加此边,返回false;
否则表明它们是2个不同的连通分量,应该合并成一个,返回true
*/
bool MergeConnectedCom( int a, int b)
{
//找到2个节点的连通分量的值
int a1= find( a);
int b1= find( b);
if ( a1 == b1)//它们已经连通了,无需再加此边,返回false;
{
return false;
}
else//将它们合并成一个,并返回true
{
p[ a1]= b1;//将一个连通分量的根节点(a1)的父亲指向另一个连通分量的根节点(b1)
return true;
}
}
int main()
{
//vEdgGrahp是所有边的向量
sort( vEdgGrahp.begin(), vEdgGrahp.end(), SortGraphEdgesByWeightAsc);//按边的权值从小到大对图的边向量排序
for ( int x= 1; x <= n; ++x) p[ x]=x;//初始时所有点都是孤立的
int iMinTreeLenCurr= 0;//已经加入到最小生成树的边向量中的边的个数
iSumMinTree= 0;//最小生成树的总长度
//按边的权值从小到大查找
for ( int i= 0; i< ( int) vEdgGrahp.size(); ++i)
{
//看它们是否需要连接起来
if ( MergeConnectedCom( aiFather, vEdgGrahp[ i].iIndexStart, vEdgGrahp[ i].iIndexEnd))
{
//连通起来,将此边加入到最小生成树的边向量中
iSumMinTree += vEdgGrahp[ i].iWeight;
++iMinTreeLenCurr;//满足条件的边的个数加1
if ( iMinTreeLenCurr == n- 1)
{
break;//跳出,已经找到了最小生成树,无需再遍历剩下的边了
}
}
}//for ( int i
//最小生成树的边的个数为n-1,表明已经将n个节点连接起来了,是连通图(即有最小生成树)
if ( iMinTreeLenCurr == n- 1)
{
printf( "%d\n", iSumMinTree);
}
else//无连通图
{
printf( "no\n");//cout<< "no"<< endl;
}
}//while
}
―――――
伪代码参考:
图边v排序;
p[ x]=x(x=1,2…n);
for ( int i= 0; i< v.size(); ++i)
{ if ( Merge(v[i].起,终))
{
iMinSpanTreeSum += 权值;
++边; if ( 边 == n- 1) break;
}
}//for ( int i
Merge(a, b)
{
a1= find( a);
b1= find( b);
if ( a1 == b1) return F;
else
{ p[ a1]= b1; return T; }
}
find(x)
{
if ( p[ x]!= x)
p[ x]= find( p[ x]);
return p[ x];
}
-----------------------------------------
实例:九度acm1347: 孤岛连通工程(已AC) http://ac.jobdu.com/problem.php?id=1347
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <vector>
using namespace std;
const int MAX_NUM_VERTICES= 10001;//最大的节点个数
typedef struct Edge
{
int iIndexStart, iIndexEnd;//边的起点、终点节点的索引
int iWeight;//边的权值
}s_Edge;//图的边
//按边的权值从小到大对图的边向量排序(return < 则从小到大)
bool SortGraphEdgesByWeightAsc( const s_Edge& a, const s_Edge& b)
{
return a.iWeight< b.iWeight;
}
/*查找当前节点所在的连通分量的根节点,并逐一更新,将遍历到的节点的父节点都指向根节点,以便下次更快地查找
return: 父节点的索引,因为是递归,所以最终是根节点的索引
*/
int FindAndUpdateFather( int*& pFather, int iIndexCurr)
{
//pFather默认是pFather[i]=i,表明每个点都是孤立的,没有连通的.
//以后,如果i,j,k连通,且k为根节点,则pFather[i]=pFather[j]=pFather[k]=k.即pFather[x]=x就表明终止了,是根节点
if ( pFather[ iIndexCurr] != iIndexCurr)
{
pFather[ iIndexCurr]= FindAndUpdateFather( pFather, pFather[ iIndexCurr]);
}
return pFather[ iIndexCurr];
}
/*将2个连通分量合并(如果它们是连通的,则返回false,否则将它们合并成一个,并返回true)
参数: pFather:链接的父亲的数组,以便进行路径压缩.
iIndex1:边的起点的下标索引
iIndex2:边的终点的下标索引
return: 如果起点所在的连通分量与起点所在的连通分量是同一个,则表明它们已经连通了,无需再加此边,返回false;
否则表明它们是2个不同的连通分量,应该合并成一个,返回true
*/
bool MergeConnectedCom( int* pFather, int iIndex1, int iIndex2)
{
//找到2个节点的连通分量的值
int a1= FindAndUpdateFather( pFather, iIndex1);
int a2= FindAndUpdateFather( pFather, iIndex2);
if ( a1 == a2)//它们已经连通了,无需再加此边,返回false;
{
return false;
}
else//将它们合并成一个,并返回true
{
pFather[ a1]= a2;//将一个连通分量的根节点(a1)的父亲指向另一个连通分量的根节点(a2)
return true;
}
}
int main()
{
int n;//节点个数(节点下标从1开始)
while ( scanf( "%d", &n) != EOF)
{
vector< s_Edge> vEdgGrahp;//图的原始边的向量,图的最小生成树的边的向量
s_Edge tmp;//临时边变量
int iNumEdges;//边的个数
//cin>> iNumEdges;
scanf( "%d", &iNumEdges);
int iSumMinTree= 0;
int aiFather[ MAX_NUM_VERTICES];//连通分量的数组
//注意memset第3个参数是 元素的个数*每个元素占的字节数,即所设置的字节数
for ( int i= 1; i<= n; ++i)
{
aiFather[ i]= i;//aiFather默认是pFather[i]=i,表明每个点都是孤立的,没有连通的.
}
int iMinTreeLenCurr= 0;//已经加入到最小生成树的边向量中的边的个数
for ( int i= 0; i< iNumEdges; ++i)//输入每条边的信息(起点索引,终点索引,边的权值)
{
//cin>> tmp.iIndexStart>> tmp.iIndexEnd>> tmp.iWeight;
scanf( "%d", &tmp.iIndexStart);
scanf( "%d", &tmp.iIndexEnd);
scanf( "%d", &tmp.iWeight);
vEdgGrahp.push_back( tmp);//将边插入到图的边向量中
}
sort( vEdgGrahp.begin(), vEdgGrahp.end(), SortGraphEdgesByWeightAsc);//按边的权值从小到大对图的边向量排序
//按边的权值从小到大查找
for ( int i= 0; i< ( int) vEdgGrahp.size(); ++i)
{
//看它们是否需要连接起来
if ( MergeConnectedCom( aiFather, vEdgGrahp[ i].iIndexStart, vEdgGrahp[ i].iIndexEnd))
{
//连通起来,将此边加入到最小生成树的边向量中
iSumMinTree += vEdgGrahp[ i].iWeight;
++iMinTreeLenCurr;//满足条件的边的个数加1
if ( iMinTreeLenCurr == n- 1)
{
break;//跳出,已经找到了最小生成树,无需再遍历剩下的边了
}
}
}//for ( int i
//最小生成树的边的个数为n-1,表明已经将n个节点连接起来了,是连通图(即有最小生成树)
if ( iMinTreeLenCurr == n- 1)
{
//cout<< iSumMinTree<< endl;
printf( "%d\n", iSumMinTree);
}
else//无连通图
{
printf( "no\n");//cout<< "no"<< endl;
}
}//while
//system("pause");
return 0;
}