后缀数组模板
我的模板是根据 罗穗骞 和 网上一模板 相结合改编而来,层次更加分明,数组名称的选择是根据用途来定义的,
总的来说应该更好理解一些:
先声明一些概念:
k-后缀数组:我这里用的是 sa[ ] ( k )
k-名次数组:我这里用的是 rank[ ] ( k )
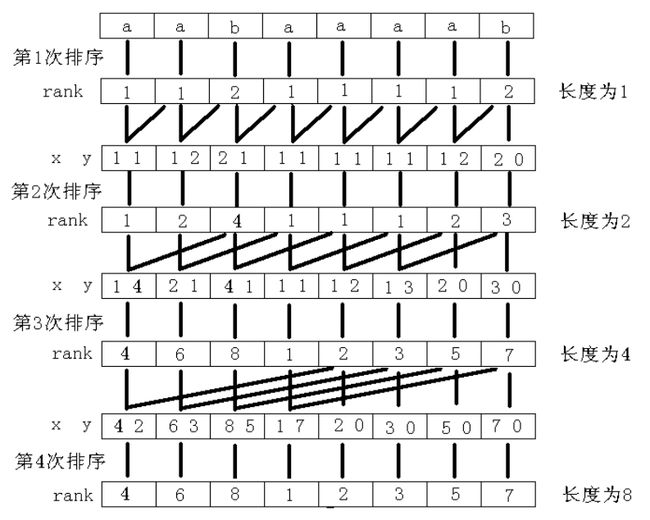
我的思路是知道rank[ ](1) 先求出sa[ ](1),然后根据 sa[ ](1) 和 rank[ ](1) 调用sorting函数求出 sa[ ](2),再求出rank[ ](2)。。。。
总的过程是rank[ ](1)---->sa[ ](1) --->rank[ ](2) ---> sa[ ](2) ---> rank[ ](k) ---->sa[ ](k)
还要注意我的数组小标全是从1开始的,程序运行前一定要初始化函数ini(),
其它该有的东西都在代码里,建议一边看代码下面的图,一边理解!
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
#define N 3000
//处理完成之后下标都是从1开始
char s[N];//存原始数据
int sum[N], rank[2*N], trank[2*N];//sum用来基数排序;trank === temp-rank
int sa[N], tsa[N]; //这里tsa[]用来保存第二关键字排序后的结果
int Top, n; //Top基数排序出现的极大值
void ini() //初始化
{
n=strlen(s);
memset(sum,0,sizeof(sum));
memset(rank,0,sizeof(rank));
memset(sa,0,sizeof(sa));
Top=128;
}
void sorting(int k)
{
int p = 1;
//利用sa排序第二关键字,求出tsa
for(int i = n-k+1; i <= n; i++) tsa[p++]=i; //超出范围的下标按下标顺序置其名次为最低
for(int i = 1; i <= n; i++) if(sa[i]>=k+1) tsa[p++]=sa[i]-k;
//按sa排名从小到大遍历,如果排名为i的某后缀(sa[i])位置在k后面,那么这个后缀肯定会在第二关键字排序
//(tsa[])中出现并且排在比较靠前的位置,这个后缀对应tsa[]中的位置为sa[i]-k
memset(sum,0,sizeof(sum));
for(int i = 1; i <= n; i++)sum[rank[i]]++;
for(int i = 1; i <= Top; i++)sum[i]+=sum[i-1];
for(int i = n; i > 0; i--)sa[sum[rank[tsa[i]]]--]=tsa[i];//这句话应该是关键
//如果把tsa[i]换成i,那么就是对rank[i]按第一关键字排序求sa[],事实上这段程序也是这样,
//不过把i换成tsa[i]后会多一个功能,就是按第一关键字排序rank相同的情况下,会按第二关键字排,
//这也正符合我们最终要求的sa[](2k)。具体方法是从tsa[n]到tsa[1],让在第二关键字排名靠后的优先
//取sum较大的,取一次,sum--,如果后边第二关键字排名靠前的某后缀在第一关键字下rank和它相同,
//那么它的sum就较小,在sa中排名就会靠前,服从排序规律!
}
void get_sa()
{
int p;
for(int i = 0; i < n; i++) rank[i+1]=s[i]; //仔细想一下,其实此时rank就是rank[](1);
for(int i = 1; i <= n; i++) sum[rank[i]]++;
for(int i = 1; i <= Top; i++) sum[i]+=sum[i-1]; //sum[i] means the number of the <= rank[i];
for(int i = n; i > 0; i--) sa[sum[rank[i]]--]=i; //sa[](1)构造完成
for(int k = 1; k <= n; k<<=1)
{
sorting(k); //由sa[](k)和rank[](k) 求 sa[](2k)
//求rank[](2k)
trank[sa[1]]=1; p=1;
for(int i = 2; i <= n; i++)
{
if((rank[sa[i]]!=rank[sa[i-1]])||(rank[sa[i]+k]!=rank[sa[i-1]+k]))p++;
trank[sa[i]]=p;
}
for(int i = 1; i <= n; i++)rank[i]=trank[i];
if(p>=n)break; //rank[1,2……n]已经唯一了,即后缀大小已经唯一确定了,不需要继续执行了
Top=p;//下次基数排序的最大值
}
}
int height[N];
void get_height()
{
for(int i = 1, j = 0; i <= n; i++)
{
if(rank[i]==1)continue;
for(;s[i+j-1]==s[sa[rank[i]-1]+j-1];)j++;//i从1开始,所以在原串中要-1
height[rank[i]]=j;
if(j>0)j--;
}
}
int *RMQ=height;
int mm[N];
int best[20][N];
void initRMQ(int n)
{
int i,j,a,b;
for(mm[0]=-1,i=1; i<=n; i++)
mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
for(i=1; i<=n; i++)best[0][i]=i;
for(i=1; i<=mm[n]; i++)for(j=1; j<=n+1-(1<<i); j++)
{
a=best[i-1][j];
b=best[i-1][j+(1<<(i-1))];
if(RMQ[a]<RMQ[b])best[i][j]=a;
else best[i][j]=b;
}
}
int askRMQ(int a,int b)
{
int t;
t=mm[b-a+1];
b-=(1<<t)-1;
a=best[t][a];
b=best[t][b];
return RMQ[a]<RMQ[b]?a:b;
}
//求sufix(a)与sufix(b)的最长公共前缀长度,用上面的RMQ优化
int lcp(int a,int b) //这里的a,b是字符串当中的位置,注意要从1开始
{
int t;
a=rank[a],b=rank[b];
if(a>b)
{
t=a;
a=b;
b=t;
}
return height[askRMQ(a+1,b)];
}
关于h[i] >= h[i-1]-1的证明:
设suffix(k)是排在suffix(i-1)前一位的后缀,则它们的最长公共前缀显然是h[i-1]。那么,suffix(k+1)显然将排在suffix(i)的前面。并且,suffix(k+1)&suffix(i) 相对于 suffix(k)&suffix(i-1)来说就是同时去掉了第一位,即少了一位的匹配数。所以suffix(i)和前一名次后缀的最长公共前缀至少是h[i-1]-1。
关于 为什么是 至少h[i-1]-1的理解:
根据上面的证明我们可以得到suffix(k+1)&suffix(i) == h[i-1]-1;
又因为suffix(k+1)显然将排在suffix(i)的前面;
所以 LCP(k+1,i) = h[i-1]-1 =min{ LCP(j-1, j) |k+1 ≤j ≤i } (LCP Theorem)<= h[i];
over