usaco training 4.3.3 Street Race 题解
Street Race题解
IOI'95
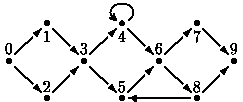
Figure 1 gives an example of a course for a street race. You see some points, labeled from 0 to N (here, N=9), and some arrows connecting them. Point 0 is the start of the race; point N is the finish. The arrows represent one-way streets. The participants of the race move from point to point via the streets, in the direction of the arrows only. At each point, a participant may choose any outgoing arrow.
Figure 1: A street course with 10 points
A well-formed course has the following properties:
- Every point in the course can be reached from the start.
- The finish can be reached from each point in the course.
- The finish has no outgoing arrows.
A participant does not have to visit every point of the course to reach the finish. Some points, however, are unavoidable. In the example, these are points 0, 3, 6, and 9. Given a well-formed course, your program must determine the set of unavoidable points that all participants have to visit, excluding start and finish.
Suppose the race has to be held on two consecutive days. For that purpose the course has to be split into two courses, one for each day. On the first day, the start is at point 0 and the finish at some `splitting point'. On the second day, the start is at this splitting point and the finish is at point N. Given a well-formed course, your program must also determine the set of splitting points. A point S is a splitting point for the well-formed course C if S differs from the star t and the finish of C, and the course can be split into two well-formed courses that (1) have no common arrows and (2) have S as their only common point, with S appearing as the finish of one and the start of the other. In the example, only point 3 is a splitting point.
PROGRAM NAME: race3
INPUT FORMAT
The input file contains a well-formed course with at most 50 points and at most 100 arrows. There are N+2 lines in the file. The first N+1 lines contain the endpoints of the arrows that leave from the points 0 through N respectively. Each of these lines ends with the number -2. The last line contains only the number -1.
SAMPLE INPUT (file race3.in)
1 2 -2 3 -2 3 -2 5 4 -2 6 4 -2 6 -2 7 8 -2 9 -2 5 9 -2 -2 -1
OUTPUT FORMAT
Your program should write two lines. The first line should contain the number of unavoidable points in the input course, followed by the labels of these points, in ascending order. The second line should contain the number of splitting points of the input course, followed by the labels of all these points, in ascending order.SAMPLE OUTPUT (file race3.out)
2 3 6 1 3
描述
图一表示一次街道赛跑的跑道。可以看出有一些路口(用 0 到 N 的整数标号),和连接这些路口的箭头。路口 0 是跑道的起点,路口 N 是跑道的终点。箭头表示单行道。运动员们可以顺着街道从一个路口移动到另一个路口(只能按照箭头所指的方向)。当运动员处于路口位置时,他可以选择任意一条由这个路口引出的街道。
图一:有 10 个路口的街道 一个良好的跑道具有如下几个特点:
- 每一个路口都可以由起点到达。
- 从任意一个路口都可以到达终点。
- 终点不通往任何路口。
- 运动员不必经过所有的路口来完成比赛。有些路口却是选择任意一条路线都必须到达的(称为“不可避免”的)。在上面的例子中,这些路口是 0,3,6,9。对于给出的良好的跑道,你的程序要确定“不可避免”的路口的集合,不包括起点和终点。
假设比赛要分两天进行。为了达到这个目的,原来的跑道必须分为两个跑道,每天使用一个跑道。第一天,起点为路口 0,终点为一个“中间路口”;第二天,起点是那个中间路口,而终点为路口 N。对于给出的良好的跑道,你的程序要确定“中间路口”的集合。如果良好的跑道 C 可以被路口 S 分成两部分,这两部分都是良好的,并且 S 不同于起点也不同于终点,同时被分割的两个部分满足下列条件:(1)它们之间没有共同的街道(2)S 为它们唯一的公共点,并且 S 作为其中一个的终点和另外一个的起点。那么我们称 S 为“中间路口 ”。在例子中只有路口 3 是中间路口。
[编辑]格式
PROGRAM NAME: race3
INPUT FORMAT:
(file race3.in)
输入文件包括一个良好的跑道,最多有 50 个路口,100 条单行道。
一共有 N+2 行,前面 N+1 行中第 i 行表示以编号为(i-1)的路口作为起点的街道,每个数字表示一个终点。行末用 -2 作为结束。最后一行只有一个数字 -1。
OUTPUT FORMAT:
(file race3.out)
你的程序要有两行输出:
第一行包括:跑道中“不可避免的”路口的数量,接着是这些路口的序号,序号按照升序排列。
第二行包括:跑道中“中间路口”的数量,接着是这些路口的序号,序号按照升序排列。
[编辑]SAMPLE INPUT
1 2 -2 3 -2 3 -2 5 4 -2 6 4 -2 6 -2 7 8 -2 9 -2 5 9 -2 -2 -1
[编辑]SAMPLE OUTPUT
2 3 6 1 3
这道图论做得不太爽,因为数据范围太小了。
既然这样,就直接搜索了。第一问太水了,和我上次说的求最小环一样,我们枚举n个点,每次把它删掉并从起点遍历。如果不能到终点,它就是一个“不可避免”的点。
第二问要稍微转一下。首先我们可以知道,第二问的解集一定是属于第一问的。
设某一点P已经是“不可避免”的点。
在刚才遍历时,我已经对从起点0开始可以到达的点全部标记过了。此时我从那个点P开始遍历,开另一个数组来标记已遍历的点。倘若有个点Q同时被遍历到,说明这两个集合有边连接,就不是“中间路口”了。
代码:(输出写得有点麻烦)
/*
PROG:race3
ID:juan1973
LANG:C++
*/
#include<stdio.h>
#include<cstring>
using namespace std;
const int maxn=51;
int num[maxn],sum[maxn],map[maxn][maxn],back[maxn][maxn];
bool that,ok1[maxn],ok2[maxn],flag[maxn],two[maxn],bre;
int n,c,del,j,i,cnt1,cnt2;
bool dfs(int k)
{
bool o=false;
if (k==n) return true;
flag[k]=true;
for (int i=1;(i<=num[k])&&(!o);i++)
{
int go=map[k][i];
if (!flag[go]&&go!=del) o=dfs(go);
}
return o;
}
void find(int k)
{
two[k]=true;
for (int i=1;i<=num[k];i++)
{
int go=map[k][i];
if (!two[go]) find(go);
}
}
int main()
{
freopen("race3.in","r",stdin);
freopen("race3.out","w",stdout);
bre=false;
while (true)
{
while (true)
{
scanf("%ld",&c);
if (c==-1) {bre=true;break;}
if (c==-2) break;
map[n][++num[n]]=c;
back[c][++sum[c]]=n;
}
if (bre) break;
n++;
}
n--;
for (del=1;del<n;del++)
{
memset(flag,0,sizeof(flag));flag[0]=true;
if (!dfs(0))
{
ok1[del]=true;cnt1++;
memset(two,0,sizeof(two));two[n]=true;
find(del);that=true;
for (i=0;i<=n;i++) if (flag[i]&&two[i]) {that=false;break;}
if (that) {ok2[del]=true;cnt2++;}
}
}
if (cnt1==0) printf("0");else printf("%ld ",cnt1);
for (i=1;(i<=n)&&(cnt1>1);i++) if (ok1[i]) {cnt1--;printf("%ld ",i);}
for (j=n;j>0;j--) if (ok1[j]) break;if (ok1[j]) printf("%ld\n",j);else printf("\n");
if (cnt2==0) printf("0");else printf("%ld ",cnt2);
for (i=1;(i<=n)&&(cnt2>1);i++) if (ok2[i]) {cnt2--;printf("%ld ",i);}
for (j=n;j>0;j--) if (ok2[j]) break;if (ok2[j]) printf("%ld\n",j);else printf("\n");
return 0;
}