HLG 2163 方格取数 (最大网络流)
题目链接: 点击打开链接
Description :
给你一个n*n的格子的棋盘,每个格子里面有一个非负数。现在从中取出若干个数,使得任意的两个数所在的格子没有公共边,就是说所取的数所在的2个格子不能相邻,并且取出的数的和最大。
Input :
包括多个测试实例,每个测试实例包括一个整数n 和n*n个非负数x(n<=20, 0 <= x <= 1000)。
Output :
对于每个测试实例,输出可能取得的最大的和。
Sample Input :
3
258 83 905
874 941 662
733 415 890
Sample Output :
3727
解析:
一开始的方法(代码):
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#define MAXN 25
#define RST(N)memset(N, 0, sizeof(N))
using namespace std;
int n, res, Max;
int Map[MAXN][MAXN], vis[MAXN][MAXN];
const int dx[] = {-1, 1, 1, -1};
const int dy[] = {1, 1, -1, -1};
int max(int x, int y) { return x>y ? x:y; }
bool check(int x, int y)
{
return x>=1&&x<=n&&y>=1&&y<=n&&!vis[x][y];
}
void solve(int px, int py)
{
int xx, yy;
vis[px][py] = 1;
//printf("%d(px), %d(py)\n", px, py);
for(int i=0; i<4; i++) {
xx = px+dx[i];
yy = py+dy[i];
if(check(xx, yy)) {
//printf("%d(xx), %d(yy) is usable\n", xx, yy);
solve(xx, yy);
}
//else printf("%d(xx), %d(yy) is XXXXXXX\n", xx, yy);
}
res += Map[px][py];
//printf("res = %d\n", res);
}
int main()
{
while(~scanf("%d", &n)) {
Max = -1;
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++) {
scanf("%d", &Map[i][j]);
}
}
if(n == 1) printf("%d\n", Map[1][1]);
else if(n == 2) {
printf("%d\n", max(Map[1][1]+Map[2][2], Map[1][2]+Map[2][1]));
}else {
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++) {
res = 0;
RST(vis);
solve(i, j);
if(res > Max) Max = res;
}
}
printf("%d\n", Max);
}
}
return 0;
}
一开始想到的方法感觉很对很对,然后过了几天重新做的时候突然想到一个过不去的情况,所以就想到了网络流;
一开始用的是深搜,思路是:
遍历二维数组中的每一个点,然后递归遍历每一个和当前点无重边的点,这种方法能测试到大多数情况;但还是菜鸟思想,因为好久没怎么刷题了,思维有点跟不上了;这种方法对于以下这种情况就测试不对了:
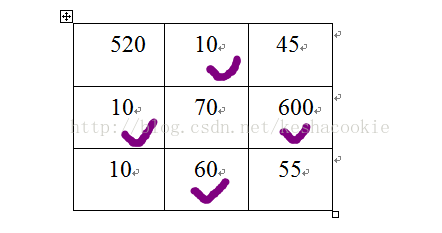
如果输入数据:
3
520 10 45
10 70 600
10 60 55
按上述方法的话会出现以下两种情况:
最后出现两种结果: 520+70+45+55+10 = 700 10+600+60+10=680
这两种答案都是错误的,因为正确的应该是: 520 + 600 + 60 = 1180
这个题由于数据范围较大,所以状态压缩过不去,需要用网络流,我重复一遍建图:
我们知道对于普通二分图来说,最大独立点集 + 最小点覆盖集 = 总点数,类似的,对于有权的二分图来说,有:
最大点权独立集 + 最小点权覆盖集 = 总点权和,
这个题很明显是要求 最大点权独立集 ,现在 总点权 已知,我们只要求出来 最小点权覆盖集 就好了,我们可以这样建图,
1,对矩阵中的点进行黑白着色(相邻的点颜色不同),从源点向黑色的点连一条边,权值为该黑色点的权值,
2,从白色的点向汇点连一条边,权值为该白色点的权值,
3,然后,对于每一对相邻的黑白点,从黑点向白点连一条边,权值为无穷大。
最后求最小割(最大流),即为最小点权覆盖集。
因为我们求出的最小割集一定是从那些相邻的黑白点之间的边(也就是不能用的边,因为相邻的数不能同时选)中选出来的,且是最小代价,也就是说从方格中拿掉的数之和尽量小,那么剩下的数之和一定是最大的。
代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <cstdlib>
#include <algorithm>
#define VM 2520
#define EM 500050
#define INF 0x3f3f3f3f
#define RST(N)memset(N, 0, sizeof(N))
using namespace std;
struct Edge
{
int u, v, nxt;
int flow;
}edge[EM << 1];
int n, m, cnt, head[VM];
int src, des, dep[VM];
void addedge(int cu, int cv, int cf)
{
edge[cnt].u = cu, edge[cnt].v = cv, edge[cnt].flow = cf;
edge[cnt].nxt = head[cu], head[cu] = cnt++;
edge[cnt].u = cv, edge[cnt].v = cu, edge[cnt].flow = 0;
edge[cnt].nxt = head[cv], head[cv] = cnt++;
}
int dir[4][2]= {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int legal(int i, int j, int k)
{
int x = i + dir[k][0];
int y = j + dir[k][1];
return x>=1 && x<=n && y>=1 && y<=m;
}
int BFS() //重新建图(按层数建图)
{
queue <int> q;
while(!q.empty()) q.pop();
memset(dep, -1, sizeof(dep));
dep[src] = 0;
q.push(src);
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i=head[u]; i!=-1; i=edge[i].nxt) {
int v = edge[i].v;
if(edge[i].flow>0 && dep[v]==-1) { // 如果可以到达但还没有访问
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[des] != -1;
}
/*
int DFS(int u,int minx) //查找路径上的最小的流量
{
if(u == des) return minx;
int tmp;
for(int i=head[u]; i!=-1; i=edge[i].nxt) {
int v = edge[i].v;
if(edge[i].flow>0 && dep[v]==dep[u]+1 && (tmp=DFS(v, min(minx, edge[i].flow)))) {
edge[i].flow -= tmp;
edge[i^1].flow += tmp;
return tmp;
}
}
return 0;
}
*/
int DFS(int u,int minx)
{
int ans = 0;
if(u == des) return minx;
for(int i=head[u]; i!=-1 && ans<minx; i=edge[i].nxt) {
int v = edge[i].v;
if(edge[i].flow>0 && dep[v]==dep[u]+1){
int tmp = min(edge[i].flow, minx-ans);
tmp = DFS(v,tmp);
ans += tmp;
edge[i].flow -= tmp;
edge[i^1].flow += tmp;
}
}
if(!ans) dep[u] = -2;
return ans;
}
int Dinic()
{
int ans = 0, tmp;
while(BFS()) {
while(1) {
tmp = DFS(src, INF);
if(tmp == 0) break;
ans += tmp;
}
}
return ans;
}
void Init()
{
m = n;
cnt = src = 0;
des = n * m + 1;
memset(head, -1, sizeof(head));
}
int main(int argc, char **argv)
{
while(~scanf("%d", &n)) {
Init();
int x, sum = 0;
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
scanf("%d", &x);
sum += x;
if((i+j)%2 == 0) {
addedge(src, (i-1)*m+j, x);
for(int k=0; k<4; k++) {
if(legal(i, j, k)) addedge((i-1)*m+j, (i+dir[k][0]-1)*m+(j+dir[k][1]), INF);
}
}else {
addedge((i-1)*m+j, des, x);
for(int k=0; k<4; k++) {
if(legal(i, j, k)) addedge((i+dir[k][0]-1)*m+(j+dir[k][1]), (i-1)*m+j, INF);
}
}
}
}
int maxflow = Dinic();
printf("%d\n", sum-maxflow);
}
return 0;
}