记录点隐马尔科夫模型(Hidden Markov Models)的点滴

因为之前HMM、最大熵、CRF接触比较少，所以最近想弥补一下这方面的知识。

有没有用HMM进行自动谱曲的？自动预测最优美的谱子出来听一听，有空我弄一个看看效果，哈哈。

这两天看完了52NLP上关于马尔科夫模型(Hidden Markov Models)的由浅入深以及coding部分的讲解，还有HMM在习性标注的几篇文章，瞬间把朴素的HMM从不懂到能够掌握90%的样子。十分感谢无私分享的人们，想想人家三四个月的学习心得分享给你，是多么值得赞扬的一件事情。

我也弄了一个List记录一下学习的顺序以及文章。为了不至于不用的时候忘了，我把一些小东西记录一下。

HMM模型的基本要素：三元组（, A, B）。

就是初始向量，t=1时刻的向量，你总得有个出发点吧，他就是了。

A是转移矩阵，转移矩阵是马尔科夫模型的基本元素，表示一个状态到另一个状态变化的可能性的大小，概率。天晴->下雨的概率，名词->动词的概率等。

矩阵就得有节点，节点其实就是隐藏的状态了，因为这些隐藏的状态你在外边看不见的，例如词性、在黑屋子里时外边的天气，这些你都看不出来的，这就是Hiden的意义了。

因为只有隐藏状态，你无法进行判别，所以只能通过观测其他显而易见的东西来间接的判别下一个状态或者序列。例如通过海藻或者咸鱼预测天气，通过了解词形进行词性标注。那怎么样建立起隐藏状态和观测状态之间的联系呢？也就是你怎么知道看到了海藻干了就能预测外边的天气呢？这就得有一个联系了，那么就是：B是混淆矩阵，是指的由隐藏状态生产观测状态的概率。

假设观测状态有M个，隐藏状态有N个，那么A的大小N*N，B的大小N*M。

经典的马尔科夫模型是有着一个不太合理的假设了，当前状态仅仅依赖于前面的状态，依赖于前面n个状态就叫做n阶马尔科夫模型，1阶用的多一点儿。

======

那么HMM能够用来做哪些事情呢？

1、评估：对于一个给定的隐马尔科夫模型其生成一个给定的观察序列的概率是多少。

想一想，毕竟隐藏状态以及转移矩阵A和混淆矩阵B都存在了，那么从初始向量开始，暴力求解一下每一种隐藏状态的组合下的概率，最后求和。这样可以解决问题，但是暴力这个东西实在是难以忍受的，特别是当状态很多，序列很长的时候。所以有了能够在记忆前面结果的基础上，继续求解当前结果的算法-前向算法。其实能够记录中间结果的算法大可以用这个动态规划的思想。
2、解码：什么样的隐藏（底层）状态序列最有可能生成一个给定的观察序列。

意思是有了观测序列，哪种隐藏状态序列的组合生产观测序列的可能性最大。其实感觉跟寻找最短路径差不多，完全可以遍历一遍，路径最短的那个结果就是。这里就是概率最大的结果，但是毕竟还是效率的问题。所以最短路径都会有很多不错的方法。同样这里也有一个-维特比算法。和前向算法差不多，不过这里要留下概率最大max的路径，并且记录来源，而不是前向算法的求和sum了。
3、学习：对于一个给定的观察序列样本，什么样的模型最可能生成该序列——也就是说，该模型的参数是什么。

这里的参数估计还是思想就是EM算法，不断的迭代直到收敛吧，即使到了局部最优解也是可以接受的嘛--前向后向算法。

而且HMM编码也是很简单，比较方便使用。下一步我在看最大熵模型，最后看看CRF。

=============

具体的应用呢，其实很多很多，经典的词性标注。想一想把HMM弄个自动谱曲的小玩意儿，应该也不错吧？改天弄一个玩玩。

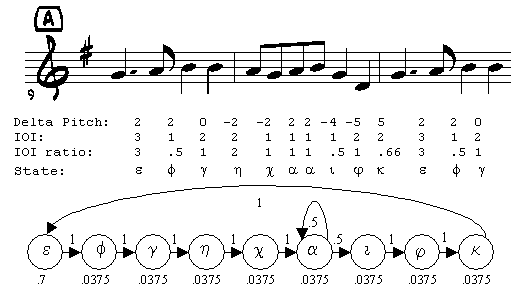
Figure 3A: Markov model for Alouette fragment