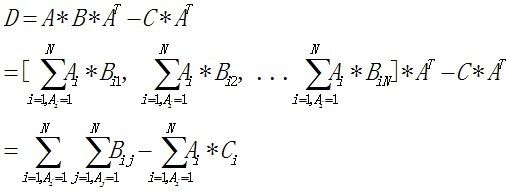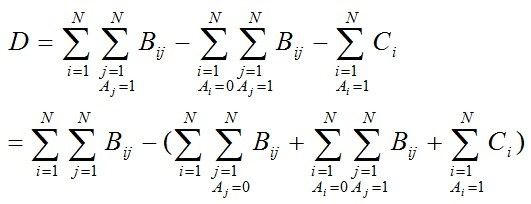2012多校联合(1
Hdu 4302 Holedox Eating
题意:一只动物在吃一根管道上的食物,每次只吃距离自己最近的,如果当前没有食物则不动,入股两侧等距都有食物则运动方向与上次相同。
解法:比赛是用了树状数组lognlogn时间查找距离某数最近的数字,其实用set就可以,每次查找前驱和后继如果前驱和后继与当前点等距则根据上次方向判断;
Hdu 4305 Lightning
一开始看题意以为是计算几何,后来发现就是“一张图去掉如干条边变成一棵树的方法数”,裸的生成树计数,基尔霍夫矩阵树定理搞定;
Hdu 4307 Matrix
题意:一个1*N的01矩阵A,给出N*N的矩阵B和N*1的矩阵C,求D=(A*B-C)*AT的最大值;
解法:
题解说由此可以看出是一个最大权闭合图模型,表示没看出来。。。
求D的最大值即求括号里三项的最小值。抽象成最小割模型(很抽象!)假设一个割将点按A[i]的值分开,设A[i]=0的点与源点在同一集合中,根据割[S,T]的容量为∑(边(u,v)的容量和(其中u∈S,∈T),可以按照如下规则构图:
点i到j有一条容量为B[i][j]的边,同时S到点i有一条容量为C[i]的边,点i到汇点有一条容量为sum [i](B矩阵第i列的和)的边,这样,图的任意一个割就和一个A一一对应,根据最大流-最小割定理便可以确定后三项和的最小值。
Hdu 4308 Saving princess claire
题意:在一个maze中经过某些点需要收费,某些点不可过,某些点之间即使不邻接也两两任意可达,问从s到t最少需要花费多少钱
解法:最短路或者bfs,可以将所有任意可达的点抽象为一个点。
Hdu 4309 Seikimatsu Occult Tonneru
题意:N个城市之间有m条路,路由三种,一种是普通的路,可通过任意数量的人,第二类路是隧道(少于20条),可以容纳若干人,第三种是桥(少于12种)一个人通过后这条路损坏,如果花费w修复后可通过任意数量的人;
解法:如果没有第三种路是一个裸的网络流,第三种路与Kaka Matrix中不同,无法估计修复后每一流量通过的费用,因此不能采用费用流;由于桥最多只有12可以2^12枚举修复哪些桥,不修复的桥没有花费,连接的边流量为1,要修复的桥则计算花费,边的流量为无穷,这样进行2^12次最大流就可以得到最优解。