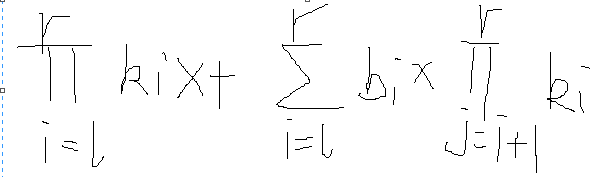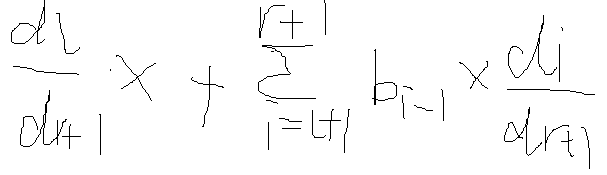bzoj 4499: 线性函数
0没有逆元!
0没有逆元!
0没有逆元!
重要的事情说三遍!
把query的式子展开就是
首先是一个看上去很对的做法:
另d[i]=PI[j=i to n] k[i]
那么答案就是
用线段树维护d,维护b[i-1]*d[i]的区间和就可以了。最后答案*d[r+1]^(-1)
但是,k可以为0,0没有逆元,所以不能这么做。
再仔细一看,第一个式子,之间生用线段树维护不就行了?水题我却做了这么久。
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#define ll long long
#define inf 1e9
#define eps 1e-8
#define md 1000000007
#define N 200010
using namespace std;
struct Tr { ll sum,k;} tr[4*N];
ll b[N],k[N];
Tr update(Tr l,Tr r)
{
return (Tr){(l.sum*r.k+r.sum)%md,l.k*r.k%md};
}
void build(int i,int l,int r)
{
if (l==r) { tr[i]=(Tr){b[l],k[l]}; return;}
int mid=(l+r)>>1;
build(i<<1,l,mid); build(i<<1|1,mid+1,r);
tr[i]=update(tr[i<<1],tr[i<<1|1]);
}
void modify(int i,int l,int r,int x,ll k,ll b)
{
if (l==r) { tr[i]=(Tr){b,k}; return;}
int mid=(l+r)>>1;
if (x<=mid) modify(i<<1,l,mid,x,k,b);
else modify(i<<1|1,mid+1,r,x,k,b);
tr[i]=update(tr[i<<1],tr[i<<1|1]);
}
Tr query(int i,int l,int r,int ql,int qr)
{
if (ql<=l&&r<=qr) return tr[i];
int mid=(l+r)>>1;
if (qr<=mid) return query(i<<1,l,mid,ql,qr);
if (mid+1<=ql) return query(i<<1|1,mid+1,r,ql,qr);
return update(query(i<<1,l,mid,ql,qr),query(i<<1|1,mid+1,r,ql,qr));
}
int main()
{
int n,m; char st[5];
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++) scanf("%lld%lld",&k[i],&b[i]);
build(1,1,n);
for (int i=1;i<=m;i++)
{
scanf("%s",st);
if (st[0]=='M')
{
int x; ll K,B;
scanf("%d%lld%lld",&x,&K,&B);
modify(1,1,n,x,K,B);
}
else
{
int l,r; ll x;
scanf("%d%d%lld",&l,&r,&x);
Tr t=query(1,1,n,l,r);
printf("%lld\n",(t.k*x+t.sum)%md);
}
}
return 0;
}