codeforces round #346 div2
Vasya lives in a round building, whose entrances are numbered sequentially by integers from 1 to n. Entrance n and entrance 1 are adjacent.
Today Vasya got bored and decided to take a walk in the yard. Vasya lives in entrance a and he decided that during his walk he will move around the house b entrances in the direction of increasing numbers (in this order entrance n should be followed by entrance 1). The negative value of b corresponds to moving |b| entrances in the order of decreasing numbers (in this order entrance 1 is followed by entrance n). If b = 0, then Vasya prefers to walk beside his entrance.
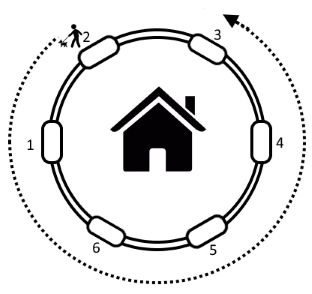Illustration for n = 6, a = 2, b = - 5.
Help Vasya to determine the number of the entrance, near which he will be at the end of his walk.
The single line of the input contains three space-separated integers n, a and b (1 ≤ n ≤ 100, 1 ≤ a ≤ n, - 100 ≤ b ≤ 100) — the number of entrances at Vasya's place, the number of his entrance and the length of his walk, respectively.
Print a single integer k (1 ≤ k ≤ n) — the number of the entrance where Vasya will be at the end of his walk.
6 2 -5
3
5 1 3
4
3 2 7
3
The first example is illustrated by the picture in the statements.
题意是：1-n成一个环，输入n,m,b。意思是m点开始，顺时针走b步走到的点是哪个
因为简单就直接贴代码。。
/*************************************************************************
> File Name: pro1.cpp
> Author: Triose
> Mail: [email protected]
> Created Time: 2016/4/16 星期六 下午 1:17:36
************************************************************************/
#include<stdio.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<iterator>
#include<math.h>
#include<stdlib.h>
#include<map>
#include<set>
using namespace std;
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff
#define inf 0x3f3f3f3f
#define rep(i,a) for((i)=0; i<(a);(i)++)
#define mem(a,b) (memset((a),b,sizeof(a)))
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define sfs(a) scanf("%s",a)
#define pf(a) printf("%d\n",a)
#define pfd(a,b) printf("%d %d\n",a,b)
#define pfs(a) printf("%s\n",a)
#define pfI(a) printf("%I64d\n",a)
#define enter putchar(10)
#define LL __int64
const double PI = acos(-1.0);
const double E = exp(1.0);
template<class T> T gcd(T a, T b) { return b ? gcd(b, a%b) : a; }
template<class T> T lcm(T a, T b) { return a / gcd(a, b)*b; }
template<class T> inline T Min(T a, T b) { return a<b ? a : b; }
template<class T> inline T Max(T a, T b) { return a>b ? a : b; }
int n, m, step;
int main() {
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
// freopen("Out.txt", "w", stdout);
#endif
while(~sft(n, m, step)) {
int ans = (m + step) % n == 0 ? n : (m + step) % n;
while(ans < 0)
ans += n;
pf(ans);
}
return 0;
}
Very soon Berland will hold a School Team Programming Olympiad. From each of the m Berland regions a team of two people is invited to participate in the olympiad. The qualifying contest to form teams was held and it was attended by n Berland students. There were at least two schoolboys participating from each of the m regions of Berland. The result of each of the participants of the qualifying competition is an integer score from 0 to 800 inclusive.
The team of each region is formed from two such members of the qualifying competition of the region, that none of them can be replaced by a schoolboy of the same region, not included in the team and who received a greater number of points. There may be a situation where a team of some region can not be formed uniquely, that is, there is more than one school team that meets the properties described above. In this case, the region needs to undertake an additional contest. The two teams in the region are considered to be different if there is at least one schoolboy who is included in one team and is not included in the other team. It is guaranteed that for each region at least two its representatives participated in the qualifying contest.
Your task is, given the results of the qualifying competition, to identify the team from each region, or to announce that in this region its formation requires additional contests.
The first line of the input contains two integers n and m (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 10 000, n ≥ 2m) — the number of participants of the qualifying contest and the number of regions in Berland.
Next n lines contain the description of the participants of the qualifying contest in the following format: Surname (a string of length from 1to 10 characters and consisting of large and small English letters), region number (integer from 1 to m) and the number of points scored by the participant (integer from 0 to 800, inclusive).
It is guaranteed that all surnames of all the participants are distinct and at least two people participated from each of the m regions. The surnames that only differ in letter cases, should be considered distinct.
Print m lines. On the i-th line print the team of the i-th region — the surnames of the two team members in an arbitrary order, or a single character "?" (without the quotes) if you need to spend further qualifying contests in the region.
5 2 Ivanov 1 763 Andreev 2 800 Petrov 1 595 Sidorov 1 790 Semenov 2 503
Sidorov Ivanov Andreev Semenov
5 2 Ivanov 1 800 Andreev 2 763 Petrov 1 800 Sidorov 1 800 Semenov 2 503
? Andreev Semenov
分析：n的范围是[2, 1e+5], m的范围是[1, 1e+4] ,所以你要开二维数组然后排序肯定不现实。实际上你只用开一个regions[1e+4]的结构体的数组存下当地区1,2,3名就可以了。。。一旦1 + 3 == 1 + 2就输出？,否则输出第一二名的名字。题目倒是不难，意思看了半天。。贴代码：
/*************************************************************************
> File Name: pro2.cpp
> Author: Triose
> Mail: [email protected]
> Created Time: 2016/4/16 星期六 下午 1:29:23
************************************************************************/
#include<stdio.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<iterator>
#include<math.h>
#include<stdlib.h>
#include<map>
#include<set>
using namespace std;
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff
#define inf 0x3f3f3f3f
#define rep(i,a) for((i)=0; i<(a);(i)++)
#define mem(a,b) (memset((a),b,sizeof(a)))
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define sfs(a) scanf("%s",a)
#define pf(a) printf("%d\n",a)
#define pfd(a,b) printf("%d %d\n",a,b)
#define pfs(a) printf("%s\n",a)
#define pfI(a) printf("%I64d\n",a)
#define enter putchar(10)
#define LL __int64
const double PI = acos(-1.0);
const double E = exp(1.0);
template<class T> T gcd(T a, T b) { return b ? gcd(b, a%b) : a; }
template<class T> T lcm(T a, T b) { return a / gcd(a, b)*b; }
template<class T> inline T Min(T a, T b) { return a<b ? a : b; }
template<class T> inline T Max(T a, T b) { return a>b ? a : b; }
int n, m;
#define N 20
struct Person {
char name[N];
int team;
int score;
};
#define M 10010
struct Regions{
Person first;
Person second;
Person third;
};
Regions r[M];
Person tmp;
int main() {
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
// freopen("Out.txt", "w", stdout);
#endif
while(~sfd(n, m)) {
for(int i = 0; i <= m; i++) {
r[i].first.score = -1;
r[i].second.score = -1;
r[i].third.score = -1;
}
for(int i = 0; i < n; i++) {
scanf("%s%d%d", tmp.name, &tmp.team, &tmp.score);
if(tmp.score > r[tmp.team].first.score) {
strcpy(r[tmp.team].third.name, r[tmp.team].second.name);
r[tmp.team].third.score = r[tmp.team].second.score;
strcpy(r[tmp.team].second.name, r[tmp.team].first.name);
r[tmp.team].second.score = r[tmp.team].first.score;
strcpy(r[tmp.team].first.name, tmp.name);
r[tmp.team].first.score = tmp.score;
}
else if(tmp.score > r[tmp.team].second.score) {
strcpy(r[tmp.team].third.name, r[tmp.team].second.name);
r[tmp.team].third.score = r[tmp.team].second.score;
strcpy(r[tmp.team].second.name, tmp.name);
r[tmp.team].second.score = tmp.score;
}
else if(tmp.score > r[tmp.team].third.score) {
strcpy(r[tmp.team].third.name, tmp.name);
r[tmp.team].third.score = tmp.score;
}
}
for(int i = 1; i <= m; i++) {
if(r[i].second.score == r[i].third.score)
pfs("?");
else {
printf("%s %s\n", r[i].first.name, r[i].second.name);
}
}
}
return 0;
}
In Berland recently a new collection of toys went on sale. This collection consists of 109 types of toys, numbered with integers from 1 to109. A toy from the new collection of the i-th type costs i bourles.
Tania has managed to collect n different types of toys a1, a2, ..., an from the new collection. Today is Tanya's birthday, and her mother decided to spend no more than m bourles on the gift to the daughter. Tanya will choose several different types of toys from the new collection as a gift. Of course, she does not want to get a type of toy which she already has.
Tanya wants to have as many distinct types of toys in her collection as possible as the result. The new collection is too diverse, and Tanya is too little, so she asks you to help her in this.
The first line contains two integers n (1 ≤ n ≤ 100 000) and m (1 ≤ m ≤ 109) — the number of types of toys that Tanya already has and the number of bourles that her mom is willing to spend on buying new toys.
The next line contains n distinct integers a1, a2, ..., an (1 ≤ ai ≤ 109) — the types of toys that Tanya already has.
In the first line print a single integer k — the number of different types of toys that Tanya should choose so that the number of different types of toys in her collection is maximum possible. Of course, the total cost of the selected toys should not exceed m.
In the second line print k distinct space-separated integers t1, t2, ..., tk (1 ≤ ti ≤ 109) — the types of toys that Tanya should choose.
If there are multiple answers, you may print any of them. Values of ti can be printed in any order.
3 7 1 3 4
2 2 5
4 14 4 6 12 8
4 7 2 3 1
In the first sample mom should buy two toys: one toy of the 2-nd type and one toy of the 5-th type. At any other purchase for 7 bourles (assuming that the toys of types 1, 3 and 4 have already been bought), it is impossible to buy two and more toys.
分析：先存下小女孩已有的玩具，从小到大排序。买玩具的时候采取贪心的策略从1~m遍历一遍，途中只会出现两种情况，已有的价格最小的玩具的价格比i大，或者等于i。分情况讨论就行了（我不知道已有的玩具有没有重复的所以加了个循环）。贴代码：
/*************************************************************************
> File Name: pro3.cpp
> Author: Triose
> Mail: [email protected]
> Created Time: 2016/4/16 星期六 下午 2:29:16
************************************************************************/
#include<stdio.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<iterator>
#include<math.h>
#include<stdlib.h>
#include<map>
#include<set>
using namespace std;
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff
#define inf 0x3f3f3f3f
#define rep(i,a) for((i)=0; i<(a);(i)++)
#define mem(a,b) (memset((a),b,sizeof(a)))
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define sfs(a) scanf("%s",a)
#define pf(a) printf("%d\n",a)
#define pfd(a,b) printf("%d %d\n",a,b)
#define pfs(a) printf("%s\n",a)
#define pfI(a) printf("%I64d\n",a)
#define enter putchar(10)
#define LL __int64
const double PI = acos(-1.0);
const double E = exp(1.0);
template<class T> T gcd(T a, T b) { return b ? gcd(b, a%b) : a; }
template<class T> T lcm(T a, T b) { return a / gcd(a, b)*b; }
template<class T> inline T Min(T a, T b) { return a<b ? a : b; }
template<class T> inline T Max(T a, T b) { return a>b ? a : b; }
int n, m;
#define N 100010
int has[N];
int buy[N];
int sum;
int main() {
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
// freopen("Out.txt", "w", stdout);
#endif
while(~sfd(n , m)) {
sum = 0;
for(int i = 0; i < n; i++)
sf(has[i]);
has[n] = INF;
sort(has, has + n);
for(int i = 1, j = 0, k = 0; m >= 0; i++) {
if(has[j] > i) {
m -= i;
if(m >= 0) {
sum++;
buy[k++] = i;
}
}
else if(has[j] == i) {
while(j < n && has[j] <= i) {
j++;
}
}
}
pf(sum);
for(int i = 0; i < sum; i++) {
printf("%d%c", buy[i], i == sum - 1 ? '\n' : ' ');
}
}
return 0;
}
Maria participates in a bicycle race.
The speedway takes place on the shores of Lake Lucerne, just repeating its contour. As you know, the lake shore consists only of straight sections, directed to the north, south, east or west.
Let's introduce a system of coordinates, directing the Ox axis from west to east, and the Oy axis from south to north. As a starting position of the race the southernmost point of the track is selected (and if there are several such points, the most western among them). The participants start the race, moving to the north. At all straight sections of the track, the participants travel in one of the four directions (north, south, east or west) and change the direction of movement only in bends between the straight sections. The participants, of course, never turn back, that is, they do not change the direction of movement from north to south or from east to west (or vice versa).
Maria is still young, so she does not feel confident at some turns. Namely, Maria feels insecure if at a failed or untimely turn, she gets into the water. In other words, Maria considers the turn dangerous if she immediately gets into the water if it is ignored.
Help Maria get ready for the competition — determine the number of dangerous turns on the track.
The first line of the input contains an integer n (4 ≤ n ≤ 1000) — the number of straight sections of the track.
The following (n + 1)-th line contains pairs of integers (xi, yi) ( - 10 000 ≤ xi, yi ≤ 10 000). The first of these points is the starting position. The i-th straight section of the track begins at the point (xi, yi) and ends at the point (xi + 1, yi + 1).
It is guaranteed that:
- the first straight section is directed to the north;
- the southernmost (and if there are several, then the most western of among them) point of the track is the first point;
- the last point coincides with the first one (i.e., the start position);
- any pair of straight sections of the track has no shared points (except for the neighboring ones, they share exactly one point);
- no pair of points (except for the first and last one) is the same;
- no two adjacent straight sections are directed in the same direction or in opposite directions.
Print a single integer — the number of dangerous turns on the track.
6 0 0 0 1 1 1 1 2 2 2 2 0 0 0
1
16 1 1 1 5 3 5 3 7 2 7 2 9 6 9 6 7 5 7 5 3 4 3 4 4 3 4 3 2 5 2 5 1 1 1
6
The first sample corresponds to the picture:
The picture shows that you can get in the water under unfortunate circumstances only at turn at the point (1, 1). Thus, the answer is 1.
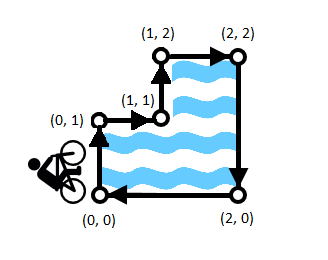
题意：给你一个多边形，问你沿着边方向有多少个顶点能够冲进多边形里面。
分析：这道题有两种做法
第一种：O(n)， 弄一个point结构体存x和y，还有到下一点的方向（0上， 1 右， 2下， 3 左）。如果相邻两个点满足<p[i].dire,p[i + 1].dire> = <1,0><2,1><3,2><0,3>，那么就会冲进去，sum++（为什么的话。。在纸上画一画吧。。。）
第二种：O(1)这个我还没看。。待会补上
第一种方法的代码：
/*************************************************************************
> File Name: pro4.cpp
> Author: Triose
> Mail: [email protected]
> Created Time: 2016/4/16 星期六 下午 3:18:22
************************************************************************/
#include<stdio.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<iterator>
#include<math.h>
#include<stdlib.h>
#include<map>
#include<set>
using namespace std;
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff
#define inf 0x3f3f3f3f
#define rep(i,a) for((i)=0; i<(a);(i)++)
#define mem(a,b) (memset((a),b,sizeof(a)))
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define sfs(a) scanf("%s",a)
#define pf(a) printf("%d\n",a)
#define pfd(a,b) printf("%d %d\n",a,b)
#define pfs(a) printf("%s\n",a)
#define pfI(a) printf("%I64d\n",a)
#define enter putchar(10)
#define LL __int64
const double PI = acos(-1.0);
const double E = exp(1.0);
template<class T> T gcd(T a, T b) { return b ? gcd(b, a%b) : a; }
template<class T> T lcm(T a, T b) { return a / gcd(a, b)*b; }
template<class T> inline T Min(T a, T b) { return a<b ? a : b; }
template<class T> inline T Max(T a, T b) { return a>b ? a : b; }
int n, m;
#define N 1010
struct point {
int x, y;
int dire;
};
point p[N];
int sum;
int main() {
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
// freopen("Out.txt", "w", stdout);
#endif
while(~sf(n)) {
sum = 0;
for(int i = 0; i <= n; i++) {
sfd(p[i].x, p[i].y);
if(i > 0) {
if(p[i].x == p[i - 1].x) {
if(p[i].y > p[i - 1].y)
p[i - 1].dire = 0;
else
p[i - 1].dire = 2;
}
else {
if(p[i].x > p[i - 1].x) {
p[i - 1].dire = 1;
}
else {
p[i - 1].dire = 3;
}
}
}
}
for(int i = 0; i < n; i++) {
if(p[i].dire == 1 && p[i + 1].dire == 0)
sum++;
else if(p[i].dire == 3 && p[i + 1].dire == 2)
sum++;
else if(p[i].dire == 2 && p[i + 1].dire == 1)
sum++;
else if(p[i].dire == 0 && p[i + 1].dire == 3)
sum++;
}
pf(sum);
}
return 0;
}