数据结构与算法1- 单链表 循环链表和跳跃链表(SkipList)
数据结构与算法1- 单链表 循环链表和跳跃链表(SkipList)
写在前面
链表是数据结构中基础数据结构,这里作为实践学习,实现和分析了单链表、循环链表和跳跃链表。
1.为什么引入链表?
传统数组实现的线性表,能够支持随机存取,即以O(1)的复杂度读写元素。传统数组方式实现存在两个弊端。
其一,在删除和插入元素时,除了要定位删除和插入的位置外,还要移动数组中其他元素,导致了很大的开销。
例如在有序表[3 4 5 7 9 13]中,删除3,则3后面的元素都将向前移动一次,共移动5次;如果要添加元素2的话,则3开始的元素都要往后端移动一次,共移动6次。假设线性表长度为n,则:
对于删除情况,假设删除n个节点的概率相同的,令X表示删除节点时元素移动次数这个随机变量,则X的平均值为:
对于插入情况,n个节点有n+1个插入位置,假设n+1个位置插入的概率相同,令Y表示插入时元素移动次数的随机变量,则Y的平均值为:
其二, 顺序数组在元素不断增长超过原先分配的连续内存区大小时,需要动态扩容时,复制元素需较大的额外开销。
基于此,引进链表来作为线性表的一种实现方式。链表在插入和删除方面,只需要找到删除或者插入位置即可,不需要移动元素,比数组开销小;当然链表不支持随机访问,这一点也是一个显著特点。
2.常见链表概念及其实现
典型的存贮无序整型值的,单链表、循环单链表、循环双链表如下图所示:
循环单链表比之于单链表区别在于,循环单链表表尾指针指向了头部,形成一个环,这样能快速找到头结点和尾结点,因此无论头插法还是尾插法,时间复杂度均为O(1);
双链表比之于单链表区别在于,双链表每个节点多了一个前向prev指针,因此一个结点能快速找到他的前驱和后继结点,对于尾部删除来讲,单链表时间复杂度为O(n),而双链表则为O(1)。
这三类表完整的操作可能因不同实现二一,c++标准库里面的链表实现方法众多,这里做出简化。
定义这三个类的的公共操作如下:
template <class T>
class List
{
public:
virtual ~List(){}
//add methods
virtual void addFromHead(const T& data)=0;
virtual void addFromTail(const T& data)=0;
//delete methods
virtual void removeFromHead()=0;
virtual void removeFromTail()=0;
virtual void remove(const T& data)=0;
//check methods
virtual bool containsOf(const T& data)=0;
virtual bool isEmpty()=0;
//get methods
virtual int getSize()=0;
//for testing,print list content
virtual void print()=0;
};
实现单链表结点定义如下:
template <class T>
class SNode
{
public:
SNode()
{
next = 0;
}
SNode(T v,SNode* n=0):data(v),next(n)
{
}
public:
T data;
SNode* next;
};
实现双链表的结点定义如下:
template<class T>
class DNode
{
public:
DNode()
{
prev = next = 0;
}
DNode(T v,DNode* p,DNode* n):data(v),prev(p),next(n)
{
}
public:
T data;
DNode *prev,*next;
};
链表实现的关键点在于: 动态的维护保存链表头结点和尾结点的指针,以及在插入删除时维护相关结点的指针。
例如有一个head和tail的单链表SLL的删除结点方法如下:
template <class T>
void SLL<T>::remove(const T& data)
{
if(head == 0)
return;
if(head->data == data)
{
removeFromHead();//delete head node
}else
{
SNode<T>* prior = head;
while(prior->next != 0 && prior->next->data != data)
prior = prior->next;
if(prior->next != 0)
{
SNode<T>* pRmove = prior->next;
prior->next = pRmove->next;
if(pRmove->next == 0)
tail = prior;//if remove last node,reset the tail
delete pRmove; //delete middle node
}
}
}例如
有一个tail指针的循环单链表CSLL删除结点方法如下:
template<class T>
void CSLL<T>::remove(const T& data)
{
if(tail != 0)
{
SNode<T> *prior=tail,*pRemove = tail->next;
while(pRemove != tail && pRemove->data != data)
{
prior = prior->next;
pRemove = pRemove->next;
}
if(pRemove != tail )
{
prior->next = pRemove->next;
delete pRemove;
}else if(tail->data == data)
{
if(tail->next == tail) //only one node
{
delete tail;
tail = 0;
}else
{
prior->next = tail->next;
delete tail;
tail = prior;
}
}
}
}
例如有一个tail指针的循环双链表CDLL删除结点方法如下:
template<class T>
void CDLL<T>::remove(const T& data)
{
if(tail != 0)
{
DNode<T>* pTmp = tail->next;
while(pTmp != tail && pTmp->data != data)
pTmp = pTmp->next;
if(pTmp != tail) //match 1..tail-1 node
{
pTmp->prev->next = pTmp->next;
pTmp->next->prev = pTmp->prev;
delete pTmp;
}else if(tail->data == data) //match tail node
{
if(tail == tail->next) //only one node
{
delete tail;
tail = 0;
}else
{
tail->prev->next = tail->next;
tail->next->prev = tail->prev;
DNode<T>* pTmp = tail->prev;
delete tail;
tail = pTmp;
}
}
}
}
这里利用C++的模板和多态机制,就可以实现由List基类指向三个链表类的实例,测试例程参见附录1。
3.跳表(SkipList)实现
这里分析并给出跳跃链表的一个实现。对于跳表的完整情况,可以参考课件:http://www.kernelchina.org/algorithm/SL.ppt,这里不再对每种操作的细节作出完整概述,而主要强调实现过程中几个注意点。
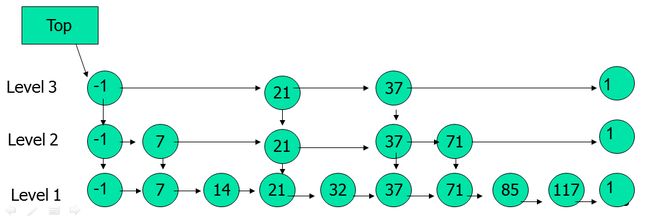
跳表如下图所示(来自课件:http://www.kernelchina.org/algorithm/SL.ppt):
1)为什么需要跳表呢?
如上图所示的跳表,当我们查找37时,top指针指向Level3,首先在第三层查找。与21比较后与37比较,查找成功,立即返回true即可。从这里即可初步看出,跳表查找的优势,如果是从具有相同元素的单链表中查找37则比较次数为5次。实际上,在最好的情况下,跳跃链表查找时间为O(lgn)。最坏情况下,所有节点都在同一级上,跳跃链表变成了正规的单链表,且查找时间为O(n)。但是跳跃链表中这种最坏情况不太可能出现,因为跳跃链表是基于随机算法的。在随机的跳跃链表中,查找时间最坏情况下也为O(lgn)。因此,跳跃链表的查找的时间复杂度即为O(lgn),比前面几种类型的链表都要优秀,因此引入跳跃链表。
2)跳跃链表的结构
如上图所示,跳跃链表的特点如下(来自:跳表(Skip List)的介绍以及查找插入删除等操作):
- 一个跳表应该有几个层(level)组成;
- 跳表的第一层包含所有的元素;
- 每一层都是一个有序的链表;
- 如果元素x出现在第i层,则所有比i小的层都包含x;
- 第i层的元素通过一个down指针指向下一层拥有相同值的元素;
- 在每一层中,-1和1两个元素都出现(分别表示INT_MIN和INT_MAX);
- Top指针指向最高层的第一个元素。
实际上在实际实现时,与上图有区别,主要在于:
1)作为泛型链表来讲,每层里面不应该设置最大和最小值来作为界限,例如上图所指的-1和1,或者是INT_MAX和INT_MIN都有可能成为实际中的值;
2)上图中,每一层都各自成为一个链表,实际上在内存结构上会被所有的层共享结点这种方式取代。
实现中的跳跃链表的内存结构如下图所示:
每个结点定义为:
#define MAX_LEVEL 16
template<class T>
class SkipNode
{
public:
SkipNode()
{
for(int i = 0;i < MAX_LEVEL ;i++)
next[i] = 0;
}
SkipNode(T k):key(k)
{
for(int i = 0;i < MAX_LEVEL ;i++)
next[i] = 0;
}
public:
T key;
SkipNode* next[MAX_LEVEL];
};
当然,每个结点里面使用MAX_LEVEL个指针,其实也需要改进,可以使用指向保存了多个指针的指针数组来解决。不过这样实现的代码,比使用数组困难些,在这里就不做讨论了。
3)跳跃链表的操作
跳跃链表要支持查找、删除和插入三种基本操作,其实现方式与普通链表存在较大的差异。
跳表定义为:
template<class T>
class SkipList
{
public:
SkipList();
~SkipList();
T* find(const T& key);
bool insert(const T& key);
bool remove(const T& key);
bool isEmpty();
void print();
private:
int getRandomLevel();
private:
int maxLevel;
typedef SkipNode<T>* SkipNodePtr;
SkipNodePtr head;
};
实现关键点在于: 维护保存跳表各层结点信息的top或者head指针,以及在插入和删除时动态维护各个节点的next指针。
课件:http://www.kernelchina.org/algorithm/SL.ppt对此作了比较好的介绍,可以参考里面的详细介绍。
基于上面的跳跃链表的内存结构给出的实现时,着重强调两点:
1)在如下图所示的有序表中查找时,有三种情况时停止:
第一种 p->next != 0 && p->next->key == key,这种情况,即找到了所查找元素的前驱;
第二种 p->next != 0 && p->next->key > key,这种情况,即找到了比所查找元素大的元素中最小的那个元素的前驱,也即所查找元素要插入位置的前驱;
第三种 p->next == 0,这种情况,表为空或者已经找到了表尾,但是所有元素都小于所要查找的元素,此时等价于找到了所查找元素要插入的位置的前驱。
这几种情况是很重要的,需要明确。
2)插入和删除结点是,都只是针对一个结点操作,在所有层上维护指针。不要以为同一个结点有多个备份链接在表中的不同层上。
另外对于同一个结点而言,要指向同一层的next结点,需要使用层号作为next指针数组的索引,例如p->next[level-1],代表的就是p结点在第level层的下一个结点;同时在向下一层展开搜索时,只需改变层的索引即可,例如: level--;p->next[level-1]即代表从当前结点p的下一层的开始比较。
跳表的查找、删除和插入三种基本操作的实现如下:
template<class T>
SkipList<T>::SkipList():maxLevel(1)
{
head = new SkipNode<T>();
}
template<class T>
T* SkipList<T>::find(const T& key)
{
int curLevel = maxLevel;
SkipNodePtr pCur = head;
while(curLevel > 0)
{
while(pCur->next[curLevel-1] != 0 && pCur->next[curLevel-1]->key < key)
pCur = pCur->next[curLevel-1];
if(pCur->next[curLevel-1] != 0 && pCur->next[curLevel-1]->key == key)
return &pCur->next[curLevel-1]->key;//if match ,return immediately
curLevel--;//search down layer
}
return 0;
}
template<class T>
bool SkipList<T>::insert(const T& key)
{
SkipNodePtr priorInsertPos[MAX_LEVEL];
int curLevel = maxLevel;
SkipNodePtr pCur = head;
while(curLevel > 0)
{
while(pCur->next[curLevel-1] != 0
&& pCur->next[curLevel-1]->key < key)
pCur = pCur->next[curLevel-1];
if(pCur->next[curLevel-1] != 0
&& pCur->next[curLevel-1]->key == key)
return false;//if already exsit ,return false
priorInsertPos[curLevel-1] = pCur;//store insert position
curLevel--;//search down layer
}
int levelCnt = getRandomLevel();//get random level count
SkipNodePtr pInsert = new SkipNode<T>(key);
//insert new node from level 1 to levelCnt
for(int i = 1;i <= levelCnt;i++)
{
if(i > maxLevel)
{
head->next[i-1] = pInsert;
}else
{
pInsert->next[i-1] = priorInsertPos[i-1]->next[i-1];
priorInsertPos[i-1]->next[i-1] = pInsert;
}
}
if(levelCnt > maxLevel)
maxLevel = levelCnt; //update max level
return true;
}
template<class T>
bool SkipList<T>::remove(const T& key)
{
SkipNodePtr priorRemovePos[MAX_LEVEL];
SkipNodePtr pRemove = 0;
int curLevel = maxLevel;
int startFindLevel = -1; //-1 represent not find
//search all levels,record position prior to remove
SkipNodePtr pCur = head;
while(curLevel > 0)
{
while(pCur->next[curLevel-1] != 0 && pCur->next[curLevel-1]->key < key)
pCur = pCur->next[curLevel-1];
if(pCur->next[curLevel-1] != 0 && pCur->next[curLevel-1]->key == key)
{
if(startFindLevel == -1)
{
startFindLevel = curLevel;
pRemove = pCur->next[curLevel-1];
}
priorRemovePos[curLevel-1] = pCur;//store pos prior to remove
}
curLevel--;//search down layer
}
if(startFindLevel == -1)
return false;
//update the reference pointer
for(int i = startFindLevel;i > 0;i--)
{
priorRemovePos[i-1]->next[i-1] = pRemove->next[i-1];
if(pRemove->next[i-1] == 0)
maxLevel--; // reduce one level,update maxLevel
}
//delete the node only onece
delete pRemove;
return true;
}
跳跃链表的测试结果参见 附录2。
参考资料:
[1] 数据结构与算法 c++版 第三版 Adam Drozdek编著 清华大学出版社
[2] 数据结构 严蔚敏 吴伟明 清华大学出版社
[3] 跳表(Skip List)的介绍以及查找插入删除等操作[4] 课件:http://www.kernelchina.org/algorithm/SL.ppt
[5] Skip List(跳跃表)原理详解与实现
附录1:链表测试结果
单链表测试: init content: SLL [3 7 4 5 9 ] remove 3: SLL [7 4 5 9 ] remove 9: SLL [7 4 5 ] contain -1?: no contain 4?: yes remove head: SLL [4 5 ] add tail 12: SLL [4 5 12 ] list size: 3 remove 5: SLL [4 12 ] remove tail: SLL [4 ] delete list: Free SLL space 循环单链表测试: init content: CSLL [3 7 4 5 9] remove 3: CSLL [7 4 5 9] remove 9: CSLL [7 4 5] contain -1?: no contain 4?: yes remove head: CSLL [4 5] add tail 12: CSLL [4 5 12] list size: 3 remove 5: CSLL [4 12] remove tail: CSLL [4] delete list: Free CSLL space 循环双链表测试: init content: CDLL [3 7 4 5 9] inverse print: CDLL [9 5 4 7 3] remove 3: CDLL [7 4 5 9] remove 9: CDLL [7 4 5] contain -1?: no contain 4?: yes remove head: CDLL [4 5] add tail 12: CDLL [4 5 12] list size: 3 remove 5: CDLL [4 12] remove tail: CDLL [4] delete list: Free CDLL space
附录2: 跳跃链表测试结果
跳跃链表测试一: SkipList [] find 12 : no insert 7: ----------------------------------- SkipList [ 3 : 7 | | 2 : 7 | | 1 : 7 ] ----------------------------------- remove 7: SkipList [] insert 12: insert 45: insert 32: ----------------------------------- SkipList [ 2 : 45 | | 1 : 12 32 45 ] ----------------------------------- remove 12: ----------------------------------- SkipList [ 2 : 45 | | 1 : 32 45 ] ----------------------------------- insert 27: insert 88: find 88 : yes ----------------------------------- SkipList [ 2 : 45 | | 1 : 27 32 45 88 ] ----------------------------------- remove 45: ----------------------------------- SkipList [ 1 : 27 32 88 ] ----------------------------------- modify element 88 to 119: ----------------------------------- SkipList [ 1 : 27 32 119 ] ----------------------------------- Free SkipList space 请按任意键继续. . . 测试结果2: insert a: insert f: insert b: insert k: insert e: insert d: ----------------------------------- SkipList [ 3 : a | | 2 : a b | | 1 : a b d e f k ] ----------------------------------- remove f: ----------------------------------- SkipList [ 3 : a | | 2 : a b | | 1 : a b d e k ] ----------------------------------- Free SkipList space 请按任意键继续. . .