POJ2195 Going Home

一.原题链接：http://poj.org/problem?id=2195

二.题目大意：给一个由H(代表房子)、m(代表人)、和 .(代表空的) 构成的矩阵。要把每个人送进房子里面，一个人只能进一个房子，人只能横着或竖着走，每个人每走一格消耗1美元，求把所有人送进房子里最少花费多少。

三.思路：把所有人和所有房子的距离先表示出来，于是这变成了一个多源多汇的求最小费用流问题，当然每条边的容量是1，因为每个人只能进去一个房子里面，然后我们当然不会傻傻地计算多源多汇，我们添加一个超级源点，跟每个人相连，容量为1，费用为0，添加一个超级汇点，每个房子跟它相连，容量为1，费用为0。求一下最小费用流。

最大流最小费用流求法：

1.把费用看做权，求一下从源点到汇点最短路（当然这条路上面要有容量）。

2.增广这条最短路，并加上费用。

3.重复1、2直到没有最短路。

证明其正确性？不会！

注意：

在构图的时候，添加费用流的时候，每条弧要分为2条方向相反，大小相反的弧，也就是要构造反向弧。为什么呢？

我们在求网络流的时候，要增加一条容量为0的反向弧，当时说目的是为了给它后悔的机会，举个例子：

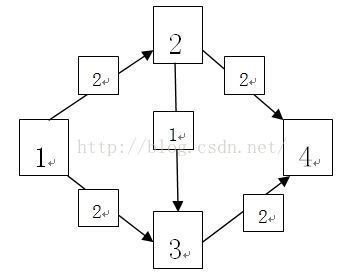
对于以下边集构成的图（第一个数和第二个数是节点，第3个数是容量， 1为源点，4为汇点）

1 2 2

1 3 2

2 3 1

2 4 2

3 4 2

没有反向弧：增广如果先增广1 2 3 4 的话，接下来只能增广1 3 4，结果只能是3。

而如果有反向弧：增广先增广1 2 3 4，接下来可以增广1 3 2 4，当然3->2有容量1，这样什么意思呢？相当于增广的是1 2 4 和 1 3 4。

而对于最小费用流来说，在进行3->2这一步的时候，相当于给其节省了花费，如果没有反向弧，就没法节省花费了。

曾经看到过，没有反向弧的网络流，就其实仅仅只是贪心。而随着本弱学习的深入，我发现其实网络流是一种DP，因为它有全局观，而且它求的是最优解。

四.代码：

#include <iostream>
#include <queue>
#include <cstring>
#include <cstdio>
#include <cmath>

using namespace std;

const int MAX_SIZE = 10000,
          INF = 0x3f3f3f3f;

struct Edge
{
    int cost, cap;
};

struct Man
{
    int i, j;
};

struct House
{
    int i, j;
};

Man men[MAX_SIZE];
House houses[MAX_SIZE];
Edge G[250][250];
int row, col, manNum, s, t, dist[MAX_SIZE],
    houseNum, nodeNum, pre[MAX_SIZE], minCost;
char mp[250][250];

void buildGraph()
{
    int i, j, w;
    manNum = houseNum = 0;
    for(i = 0; i < row; i++)
        for(j = 0; j < col; j++)
            if('m' == mp[i][j]){
                men[++manNum].i = i;
                men[manNum].j = j;
             }
             else if('H' == mp[i][j]){
                houses[++houseNum].i = i;
                houses[houseNum].j = j;
             }

    s = houseNum + manNum + 1, t = s + 1;
    nodeNum = t;

    memset(G, 0, sizeof(G));

    for(i = 1; i <= manNum; i++){
        G[s][i].cap = 1;
        for(j = 1; j <= houseNum; j++){
            w = abs(men[i].i - houses[j].i) +
                abs(men[i].j - houses[j].j);
            G[i][j+manNum].cap = 1;
            G[i][j+manNum].cost = w;
            G[j+manNum][i].cost = -w;
        }
    }

    for(j = 1; j <= houseNum; j++)
        G[j+manNum][t].cap = 1;
}

bool SPFA(int s)
{
    int i, j, cur, cnt[MAX_SIZE];
    bool inQue[MAX_SIZE];
    queue <int> que;
    memset(dist, INF, sizeof(dist));
    memset(cnt, 0, sizeof(cnt));
    memset(pre, -1, sizeof(pre));
    memset(inQue, 0, sizeof(inQue));
    dist[s] = 0;
    que.push(s);
    inQue[s] = true;
    cnt[s]++;
    while(!que.empty()){
        cur = que.front();
        que.pop();
        inQue[cur] = false;
        for(i = 1; i <= nodeNum; i++){
            if(G[cur][i].cap &&
               dist[i] > dist[cur] + G[cur][i].cost){
                dist[i] = dist[cur] + G[cur][i].cost;
                pre[i] = cur;
                if(!inQue[i]){
                    que.push(i);
                    inQue[i] = true;
                    cnt[i]++;
                    if(cnt[i] > nodeNum)
                        break;
                }
            }
        }
    }

    return pre[t] != -1;
}

void ford_fulkerson(int s,int t)
{
    int i, j, u, v, minFlow;
    while(SPFA(s)){
        minCost += dist[t];
        minFlow = INF;
        for(u = pre[t], v = t; u != -1; v = u, u = pre[u])
            minFlow = min(G[u][v].cap, minFlow);

        for(u = pre[t], v = t; u != -1; v = u, u = pre[u]){
            G[u][v].cap -= minFlow;
            G[v][u].cap += minFlow;
        }
    }
}

int main()
{
    //freopen("in.txt", "r", stdin);
    int i, j;
    while(~scanf("%d%d", &row, &col)){
        if(!row && !col)
            break;
        for(i = 0; i < row; i++)
            scanf("%s", mp[i]);
        minCost = 0;
        buildGraph();
        ford_fulkerson(s, t);
        printf("%d\n", minCost);
    }
}