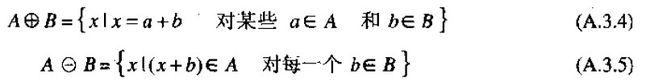二值形态学(膨胀,腐蚀,开启,关闭)的数学概念介绍
1.引言
形态学一般指生物学中研究动物和植物结构的分支。数学形态学(也称图像代数)表示以形态为基础对图像进行分析的数学工具。他的基本思想是用具有一定形态的结构元素去量度和提取图像中的对应形状以达到对图像分析和识别的目的。数学形态学的数学基础和所用的语言是集合论。数学形态学的应用可以简化图像数据,保持他们基本的形状特征,并出去不相干的结构。数学形态学的算法有天然的并行实现的结构。
在图像处理方面,二值形态学经常应用到对图像进行分割,细化,抽取骨架,边缘提取,形状分析,角点检测,分水岭算法等等。由于其算法简单,算法能够并行运算所以经常应用到硬件中。
2.数学形态学
数学形态学的基本运算有4个:膨胀/扩张(erode)、腐蚀/侵蚀(dilate)、开启(open)和关闭(close)。
2.1 膨胀,腐蚀,开启,关闭的概念和作用
膨胀是将与物体接触的所有背景点合并到该物体中,使边界向外部扩张的过程。可以用来填补物体中的空洞。
腐蚀是一种消除边界点,使边界向内部收缩的过程。可以用来消除小且无意义的物体。
开启是先腐蚀后膨胀的过程。用来消除小物体、在纤细点处分离物体、平滑较大物体的边界的同时并不明显改变其面积。
关闭是先膨胀后腐蚀的过程。用来填充物体内细小空洞、连接邻近物体、平滑其边界的同时并不明显改变其面积。
表达式是![]()
2.2 膨胀,腐蚀的数学运算
膨胀运算举例,(a)是背景图片,(b)结构元素,(c)是结构元素的对偶,(d)是(a)和(b)膨胀之后的结果。
膨胀运算是将(a)分别沿结构元素(b)的对偶(c)移动,然后将3次移动后的位置并起来,就得到膨胀的结果(d)。
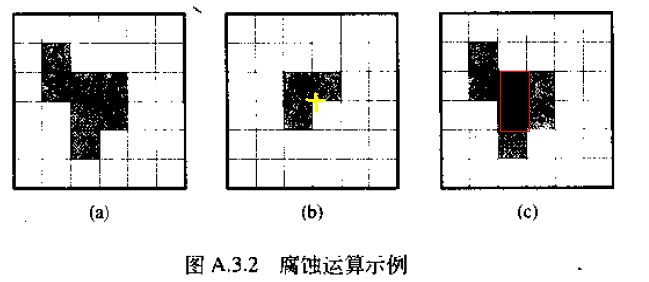
腐蚀运算举例,(a)是背景图片,(b)是结构元素,(c)中深黑色是腐蚀运算的结果。
腐蚀运算是(a)分别沿着(b)中3个元素的向量移动,然后将3次移动的部分的交集就是腐蚀结果(c)。
用向量表示膨胀和腐蚀运算的过程:
膨胀就是A和B的元素分别相加,然后去去重,并集。
腐蚀就是A中元素分别加上B所有的元素,结果还属于A,则这样的元素就是A和B膨胀的结果。
2.3 开启和闭合的数学运算
背景图片(a)和结构元素(b):
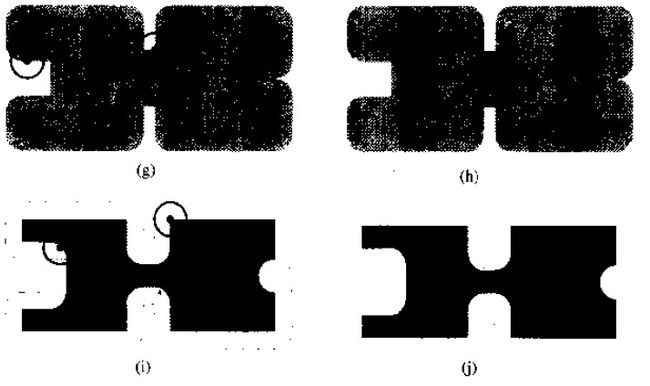
开启运算:
关闭运算:
参考资料:
图像工程(上册),章毓晋,清华大学出版社