UVALive - 3305 Tour 双调欧几里得旅行商问题

题意：真心想不出好的动态转移方程，看了题解原来是双调欧几里得旅行问题

思路【转】：

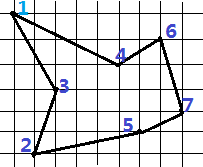
  欧几里得旅行商问题是对平面上给定的n个点确定一条连接各点的最短闭合旅程的问题。如图（a）给出了一个7个点问题的解。这个问题的一般形式是NP完全的，故其解需要多于多项式的时间。

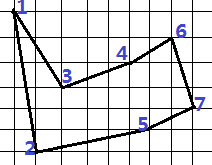
J.L. Bentley 建议通过只考虑双调旅程(bitonic tour)来简化问题,这种旅程即为从最左点开始，严格地从左到右直至最右点，然后严格地从右到左直至出发点。下图(b)显示了同样的7个点的最短双调路线。在这种情况下，多项式的算法是可能的。事实上，存在确定的最优双调路线的O(n*n)时间的算法。

 图a            图b

注:在一个单位栅格上显示的平面上的七个点。 a)最短闭合路线,长度大约是24.89。这个路线不是双调的。b)相同点的集合上的最短双调闭合路线。长度大约是25.58。

这是一个算导上的思考题15-1。

首先将给出的点排序，关键字x，重新编号，从左至右1，2，3，…，n。

定义p[i][j]，表示结点i到结点j之间的距离。

定义d[i][j]，表示从i连到1，再从1连到j，（注意，i>j，且并没有相连。）

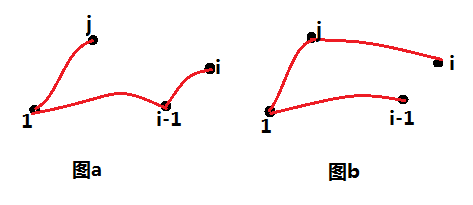
对于任意一个点i来说，有两种连接方法，一种是如图（a）所示，i与i-1相连，另一种呢是如图（b），i与i-1不相连。

根据双调旅程，我们知道结点n一定与n相连，那么，如果我们求的d[n][n-1]，只需将其加上p[n-1][n]就是最短双调闭合路线。

根据上图，很容易写出方程式：

dp[i][j]=dp[i-1][j]+dist[i][i-1];

dp[i][i-1]=min(dp[i][i-1],dp[i-1][j]+dist[j][i]);

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int MAXN = 101;

struct point{
    int x,y;
}p[MAXN];
int n;
double dp[MAXN][MAXN],a[MAXN][MAXN];
double dis(point p1,point p2){
    return sqrt((double)(p1.x-p2.x)*(p1.x-p2.x)+(double)(p1.y-p2.y)*(p1.y-p2.y));
}

int main(){
    while (scanf("%d",&n) != EOF){
        for (int i = 0; i < n; i++)
            scanf("%d%d",&p[i].x,&p[i].y);
        if (n == 1){
            printf("0.00\n");
            continue;
        }
        for (int i = 0; i < n; i++){
            a[i][i] = 0;
            for (int j = i+1; j < n; j++)
                a[i][j] = a[j][i] = dis(p[i],p[j]);
        }
        dp[0][0] = 0;
        for (int i = 1; i < n; i++)
            dp[i][0] = a[i][0];
        for (int i = 1; i < n-1; i++){
            dp[i+1][i] = 0x3f3f3f3f;
            for (int j = 0; j <= i-1; j++){
                dp[i+1][j] = dp[i][j] + a[i][i+1];
                dp[i+1][i] = min(dp[i+1][i],dp[i][j]+a[j][i+1]);
            }
        }
        printf("%.2lf\n",dp[n-1][n-2]+a[n-1][n-2]);
    }
    return 0;

}