数据结构之图- 图的表示方法(6)
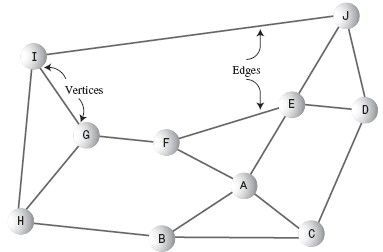
Graphs is composed by vertices and edges. We can look at Internet as a graph, which webpage are vertices and hyperlinks are edges.
Why doesn't the Java Collections API include a Graph implementation?
I don’t know why there is no graph library within the JDK , but I guess Sun decided to leave this to developers, since most applications that require graphs also require very unique implementations. Also as graphs can have so many different forms and flavours with wildly different characteristics, a general Graph might not turn out to be very useful. But we can use Graph libraries like:JGraphT
0 Graph Types
1) Unconnected graph and connected graph(非连通图和连通图)
2) undirected graph and directed graph(无向图和有向图)
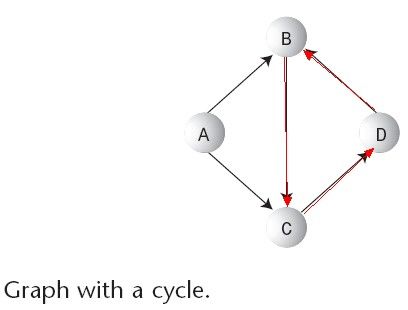
3) graph with cycles and graph without cycles(有环图和无环图)
graph with cycles: a path that ends up where it started. Like the following figure, the path B-C-D-B forms a cycle. (Notice that A-B-C-A is not a cycle because you can’t go from C to A.). It’s easy to figure out if a non-directed graph has cycles. If a graph with N nodes has more than N-1 edges, it must have cycles.
A graph with no cycles is called a tree. The binary and multiway trees we saw earlier in this book are trees in this sense. However, the trees that arise in graphs are more general than binary and multiway trees, which have a fixed maximum number of child nodes.
A tree is a graph with no cycles.
Somtimes DAG is shorted for a directed acyclic graph(有向无环图)
4) Unweighted graph and weighted graph(非加权图和加权图)
1 Vertices
It is usually convenient to represent a vertex by an object of a vertex class. For instance:
/**
* Fuction:
*
* @author zhonghua
* @version 2013-3-9 下午3:15:44
* @since 1.0
*/
public class Vertex {
public char label;
//mark a vertex is visited or not; true:visited,false:unvisited
public boolean wasVisited;
public Vertex(char lab){
label=lab;
wasVisited=false;
}
@Override
public int hashCode() {
final int prime = 31;
int result = 1;
result = prime * result + label;
result = prime * result + (wasVisited ? 1231 : 1237);
return result;
}
@Override
public boolean equals(Object obj) {
if (this == obj)
return true;
if (obj == null)
return false;
if (getClass() != obj.getClass())
return false;
Vertex other = (Vertex) obj;
if (label != other.label)
return false;
if (wasVisited != other.wasVisited)
return false;
return true;
}
@Override
public String toString() {
return "Vertex [label=" + label + ", wasVisited=" + wasVisited + "]";
}
} //end class Vertex
2 Edges
Two methods are commonly used for graphs: the adjacent matrix andthe adjacent list. Remember that one vertex is said to be adjacent to another if they're connected by a single edge.
2.1 The Adjacent Matrix
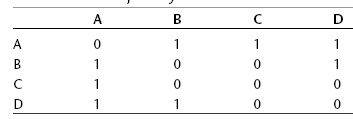
An adjacency matrix is a two-dimensional array in which the elements indicate whether an edge is present between two vertices. If a graph has N vertices, the adjacency
matrix is an NxN array. Table below shows the adjacency matrix for the graph in Figure a.
The vertices are used as headings for both rows and columns. An edge between two vertices is indicated by a 1; the absence of an edge is a 0. (You could also use Boolean
true/false values.)
Note that the triangular-shaped part of the matrix above the identity diagonal is a mirror image of the part below; both triangles contain the same information. This redundancy may seem inefficient, but there’s no convenient way to create a triangular array in most computer languages, so it’s simpler to accept the redundancy. Consequently, when you add an edge to the graph, you must make two entries in the adjacency matrix rather than one.
2.2 The Adjacency List
The other way to represent edges is with an adjacency list. The list in adjacency list refers to a linked list. Actually, an adjacency list is an array of lists (or sometimes a list of lists). Each individual list shows what vertices a given vertex is adjacent to. Table below shows the adjacency lists for the graph of Figure a.
In this table, the —> symbol indicates a link in a linked list. Each link in the list is a vertex. Here the vertices are arranged in alphabetical order in each list, although that’s not really necessary. Don’t confuse the contents of adjacency lists with paths. The adjacency list shows which vertices are adjacent to—that is, one edge away from—a given vertex, not paths from vertex to vertex.
3 Representing a Graph in a Program
The Graph Class
/**
* Fuction:
* Representing a Graph in a Program
* @author zhonghua
* @version 2013-3-9 下午3:53:27
* @since 1.0
*/
public class Graph {
private final int MAX_VERTS=20;
private Vertex arrVertex[]; //array of vertices
private int adjMat[][]; //adjacency matrix
private int nVerts; //current number of vertices
// ------------------------------------------------------------
public Graph(){
arrVertex=new Vertex[MAX_VERTS];
adjMat=new int[MAX_VERTS][MAX_VERTS];
nVerts=0;
//set adjacency
for(int i=0;i<MAX_VERTS;i++){
for(int j=0;j<MAX_VERTS;j++)
adjMat[i][j]=0;
} //end for
}
// ------------------------------------------------------------
public void addVertex(Vertex vertex){
arrVertex[nVerts++]=vertex;
}
// ------------------------------------------------------------
public void addEdge(int start,int end){
adjMat[start][end]=1;
adjMat[end][start]=1;
}
// ------------------------------------------------------------
public void display(int v){
System.out.println(arrVertex[v].toString());
}
// ------------------------------------------------------------
} //end class Graph