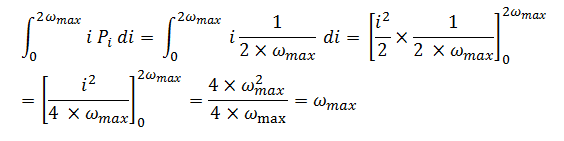A brief explanation about the resampling wheel in CS373 PROGRAMMING A ROBOTIC CAR
At this week's Programming a robotic car class, there is a slightly difficult concept about how to implement resampling particles procedure.
And according to Prof. Sebastian Thrun. We have a magical wheel to resample the particles in terms of their important weight.
But this approach contains many magic steps. As for me, there are two questions:
- Why we add the beta by a uniform distributed random number in [0, 2*Wmax]
- What the purpose of the if else pseudo code
And there is my explanation of this algorithm.
First of all, let's consider what we actually do by adding the random number to beta. With the definition of expectation, we know the expectation of U{0...2*Wmax} is
hence, we know we add Wmax to beta in each iteration.
Then, let's look an example:
This is an pie diagram that contains 3 slice. And consider we start at index_1, and we add Wmax, that is 50% to beta, then we comes to the position of index_2. Therefore, by adding up the beta with Wmax, we can reach any point in the pie. That means we can pick up any slice to which the arrow pointed by the probability/area. Thus, the first question got its answer
As for question 2, it's actually a while loop instead of the if test, and we just treat the beta as the location to which the arrow pointed in the pie diagram I posted. And you will find that it's just find the index of the slice of this location located in, and then return this index.
==========================================================================================================================
While this is a simple approach, there are a bunch of solution for particle filter resampling. You can find the information of some comparison in this paper and A simple explanation about some of them at here
Again, we have many talented student in this class and they have find some even more powerful solution to this problem, you can follow this thread