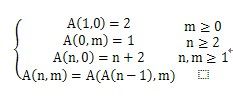递归

一个直接或间接地调用自身的算法称为递归算法。一个使用函数自身给出定义的函数称为递归函数。在计算机算法设计与分析中，使用递归技术往往使函数的定义和算法的描述简捷且易于理解。有些数据结构如二叉树等，由于其本身固有的递归特性，特别适合用递归的形式来描述。还有一些问题，虽然其本身并没有明显的递归结构，但用递归技术来求解使设计出的算法简洁易懂且易于分析。
关于递归的例子

1 阶乘函数

2 Fibonacci数列

3 Ackerman函数

4 排列问题

设R={r1,r2,...,rn}是要进行排列的n个元素，Ri=R-{ri}。集合X中元素的全排列记为Perm(X)。(ri)Perm(X)表示在全排列Perm(X)的每一个排列前加上前缀ri得到的排列

5 整数划分问题

将一个正整数n表示成一系列正整数之和

n=n1+n2+...+nk(其中，n1>=n2>=...>=nk>=1，k>=1)

正整数n的一个这种表示称为正整数n的一划分。正整数n的不同划分个数称为正整数n的划分数，记作p(n)

在正整数n的所有不同的划分中，将最大加数n1不大于m的划分个数记作q(n,m)。我们可以建立如下递归关系。

(1) n>=1，则q(n1,1)=1

由定义知n1<=1

又n>=1且n1是整数

所以n1=1

所以只有一种划分

(2)m>=n则 q(n1,m)=q(n,n)

由定义知n1<=m

又m>=n

所以n1=n

所以只有一种划分

(3) q(n1,n)=1+q(n1,n-1)

由定义知n1<=n

当n1=n时,由(2)知q(n,n)=1

当n1<n时，又n1属于整数

所以n1<=n-1

所以等价于q(n1,n-1)

综上所述

q(n1,n)=1+q(n1,n-1)

(4)n>m>1,q(n1,m)=q(n1,m-1)+q(n1-m,m)

...

参考http://www.cnblogs.com/dolphin0520/archive/2011/04/04/2005098.html

    整数划分问题是算法中的一个经典命题之一，有关这个问题的讲述在讲解到递归时基本都将涉及。所谓整数划分，是指把一个正整数n写成如下形式：

    n=m1+m2+...+mi; （其中mi为正整数，并且1 <= mi <= n），则{m1,m2,...,mi}为n的一个划分。

如果{m1,m2,...,mi}中的最大值不超过m，即max(m1,m2,...,mi)<=m，则称它属于n的一个m划分。这里我们记n的m划分的个数为f(n,m);

例如但n=4时，他有5个划分，{4},{3,1},{2,2},{2,1,1},{1,1,1,1};

注意4=1+3 和 4=3+1被认为是同一个划分。

该问题是求出n的所有划分个数，即f(n, n)。下面我们考虑求f(n,m)的方法;

1.递归法：

   根据n和m的关系，考虑以下几种情况：

   (1)当n=1时，不论m的值为多少（m>0)，只有一种划分即{1};

   (2)当m=1时，不论n的值为多少，只有一种划分即n个1，{1,1,1,...,1};

   (3)当n=m时，根据划分中是否包含n，可以分为两种情况：

      (a)划分中包含n的情况，只有一个即{n}；

      (b)划分中不包含n的情况，这时划分中最大的数字也一定比n小，即n的所有(n-1)划分。

      因此 f(n,n) =1 + f(n,n-1);

   (4)当n<m时，由于划分中不可能出现负数，因此就相当于f(n,n);

   (5)但n>m时，根据划分中是否包含最大值m，可以分为两种情况：

       (a)划分中包含m的情况，即{m, {x1,x2,...xi}}, 其中{x1,x2,... xi} 的和为n-m，因此这情况下

          为f(n-m,m)

       (b)划分中不包含m的情况，则划分中所有值都比m小，即n的(m-1)划分，个数为f(n,m-1);

      因此 f(n, m) = f(n-m, m)+f(n,m-1);

      综上所述：

                             f(n, m)=   1;              (n=1 or m=1)

               f(n,m)   =    f(n, n);                   (n<m)

                             1+ f(n, m-1);              (n=m)

                             f(n-m,m)+f(n,m-1);         (n>m)