POI 2006 Met-Subway

 

Subway

Memory limit: 128 MB

A certain city has been coping with subway construction for a long time. The finances have been mismanaged and the costs have been underestimated to such extent that no funds were foreseen for the purchase of trains. As a result, too many stations and only some of the planned tunnels have been built - barely enough to allow a connection between any two stations to exist. The number of tunnels (each of them is bidirectional) is one less than the number of stations built. From the remaining funds only a handful of trains have been acquired.

To save their face the board of directors have asked you to plan subway routes in such a way as to allow maximal number of stations to be connected. Each train travels on a specified route. The routes cannot branch (no three tunnels starting at a single station may belong to the same route). Distinct routes may comprise the same station or tunnel.

Task

Write a programme which:

• reads a description of the tunnel system and the number of subway lines, which are to be planned from the standard input,
• calculates the maximal number of stations which can be covered by the specified number of subway lines,
• writes the outcome to the standard output.

Input

The first line of the standard input contains two integers and ( , ) separated by a single space. The number denotes the number of stations and the number denotes the number of subway lines, which are to be planned. The stations are numbered from 1 to .

Each of the following lines contains two distinct integers separated by a single space. The numbers in the -th line denote the numbers of stations connected by -th tunnel.

Output

The first and only line of the standard output should contain a single integer denoting the maximal number of stations which can be covered by train routes.

For the input data:

17 3



1 2



3 2



2 4



5 2



5 6



5 8



7 8



9 8



5 10



10 13



13 14



10 12



12 11



15 17



15 16



15 10

the correct outcome is:

13

The figure represents the tunnel system (with subway routes marked) in one of the optimal configurations.

 

(from: http://www.oi.edu.pl/php/show.php?ac=e180602&module=show&file=zadania/oi13/met&print=yes )

 

首先证明，存在最优解，使得所有路径形成一棵树：

 

假设路径由两部分组成，则可以找到两个点V1、V2，使得X1-V1-Y1、X2-V2-Y2均为一条路径，那么连接V1、V2，并把X1-V1-V2-X2、Y1-V1-V2-Y2作为两条新路经，路径总数不变，解不会变差。

 

 

其次，对于原树上的一条最长链， 一定存在一个最优解，包含这条链：

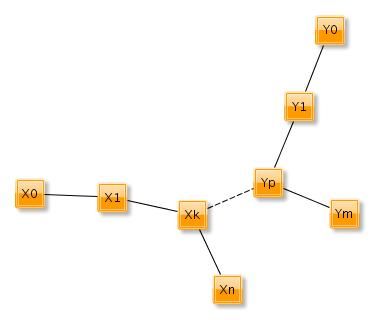
如图，设X0,X1,...,Xn是当前解中的一条链，Y0,Y1,..Ym是原树的最长链（m>n 且 X0、Xn、Y0、Ym为叶结点），Xk是一个度不小于3的节点。

不妨设在X0..Xk，Xk..Xn中较短链为X0..Xk，Y0..Yp，Yp..Ym中较长链为Y0..Yp，那么沿Xn向父节点删除节点直到一个度不小于3的节点，再把Xk-Yp-...-Y0加入，得到的新解不比原来的差。

 

 

 

如果要用k条路径覆盖一棵树，叶结点最多2k个；而如果有2k个叶结点，通过归纳法可以证明，一定存在一个用k条路径覆盖所有节点的方案。因此可以把最长链的一个端点作为根建立有根树，原问题转化为从根出发寻找2l-1条路径使得覆盖的点最多，可以贪心解决。我的实现是O(n + l log n)的，其实还存在O(n)的实现。

 

 

附上源代码：

/* * $File: p1517.cpp * $Date: Wed Jun 09 20:11:30 2010 +0800 * * Source: POI 2006 Met-subway * */ #define INPUT "p1517.in" #define OUTPUT "p1517.out" #include <cstdio> namespace Solve { const int NVTX_MAX = 1000005, NARC_MAX = NVTX_MAX * 2; struct Arc { int tvtx, usable, next; }; Arc arc[NARC_MAX]; int graph[NVTX_MAX], nvtx, narc; int get_maxchain(); struct Node { int par, child, sibling, ml_dep, ml_vtx; // max leaf }; Node tree[NVTX_MAX]; void dfs_mktree(int v0); int work(int tnleaf); void insert_arc(int u, int v); namespace Heap { struct Node { int key, id; }; Node heap[NVTX_MAX]; int size; void insert(int key, int id); void extract_min(); } void solve(FILE *fin, FILE *fout); } void Solve::solve(FILE *fin, FILE *fout) { const int BUFFER_LEN = 1024 * 1024 * 5; static char buffer[BUFFER_LEN]; char *ptr = buffer, *buf_end = ptr + 1; #define PTR_NEXT() / { / ptr ++; / if (ptr == buf_end) / { / ptr = buffer; / buf_end = buffer + fread(buffer, 1, BUFFER_LEN, fin); / } / } #define READ_INT(_x_) / { / while ((*ptr < '0' || *ptr > '9') && *ptr != '-') / PTR_NEXT(); / bool _nega_ = false; / if (*ptr == '-') / { / _nega_ = true; / PTR_NEXT(); / } / int register _n_ = 0; / while (*ptr >= '0' && *ptr <= '9') / { / _n_ = _n_ * 10 + *ptr - '0'; / PTR_NEXT(); / } / if (_nega_) / _n_ = - _n_; / (_x_) = (_n_); / } #define READ_UP_CHAR(_c_) / { / while (*ptr < 'A' || *ptr > 'Z') / PTR_NEXT(); / (_c_) = *ptr; / PTR_NEXT(); / } PTR_NEXT(); narc = 1; int l; READ_INT(nvtx); READ_INT(l); for (int i = 1; i < nvtx; i ++) { int a, b; READ_INT(a); READ_INT(b); insert_arc(a, b); insert_arc(b, a); } fprintf(fout, "%d/n", work(l << 1)); #undef PTR_NEXT #undef READ_INT #undef READ_UP_CHAR } void Solve::insert_arc(int u, int v) { narc ++; arc[narc].tvtx = v; arc[narc].usable = 1; arc[narc].next = graph[u]; graph[u] = narc; } int Solve::work(int tnleaf) { if (tnleaf == 0) return 0; if (nvtx == 1) return 1; int root = get_maxchain(); dfs_mktree(root); int ans = 1; for (int i = tree[root].child; i; i = tree[i].sibling) Heap::insert(-tree[i].ml_dep, tree[i].ml_vtx); while ((-- tnleaf) && Heap::size) { int v = Heap::heap[0].id; Heap::extract_min(); for (int i = v; i != root; i = tree[i].par) { ans ++; if (tree[i].par != root) { for (int j = tree[tree[i].par].child; j; j = tree[j].sibling) if (i != j) { Heap::insert(-tree[j].ml_dep, tree[j].ml_vtx); tree[j].par = root; } } } } return ans; } void Solve::Heap::insert(int key, int id) { Node n0; n0.key = key; n0.id = id; int register root = size ++; while (root) { int register par = (root - 1) >> 1; if (n0.key < heap[par].key) { heap[root] = heap[par]; root = par; } else break; } heap[root] = n0; } void Solve::Heap::extract_min() { Node n0 = heap[-- size]; int register root = 0; while (1) { int register ch = (root << 1) + 1, ch1 = (root + 1) << 1; if (ch1 < size && heap[ch1].key < heap[ch].key) ch = ch1; if (ch < size && heap[ch].key < n0.key) { heap[root] = heap[ch]; root = ch; } else { heap[root] = n0; return; } } } void Solve::dfs_mktree(int v0) { struct Var { int i, v0, ml_dep, ml_vtx, child; }; static Var stack[NVTX_MAX]; int nstack = 0; #define CALL(_v_) / do / { / static Var *s; / s = &stack[nstack ++]; / s->i = graph[(_v_)]; / s->v0 = (_v_); / s->ml_dep = 0; / s->ml_vtx = (_v_); / s->child = 0; / goto FUNC_INIT; / } while (0) #define RET() / do / { / static const Var *s; / s = &stack[-- nstack]; / static Node *t; / t = &tree[s->v0]; / t->ml_dep = s->ml_dep; / t->ml_vtx = s->ml_vtx; / t->child = s->child; / if (!nstack) / goto FUNC_OUT; / goto FUNC_RET; / } while (0) CALL(v0); while (1) { int t; Var *v; FUNC_INIT: v = &stack[nstack - 1]; for (; v->i; v->i = arc[v->i].next) if (arc[v->i].usable) { arc[v->i ^ 1].usable = 0; t = arc[v->i].tvtx; tree[t].par = v->v0; tree[t].sibling = v->child; v->child = t; CALL(t); FUNC_RET: v = &stack[nstack - 1]; t = arc[v->i].tvtx; if (tree[t].ml_dep > v->ml_dep) { v->ml_dep = tree[t].ml_dep; v->ml_vtx = tree[t].ml_vtx; } } v->ml_dep ++; RET(); } FUNC_OUT: ; /* Node &n0 = tree[v0]; n0.ml_dep = 0; n0.ml_vtx = v0; for (int i = graph[v0]; i; i = arc[i].next) if (arc[i].usable) { arc[i ^ 1].usable = 0; int t = arc[i].tvtx; tree[t].par = v0; tree[t].sibling = n0.child; n0.child = t; dfs_mktree(t); if (tree[t].ml_dep > n0.ml_dep) { n0.ml_dep = tree[t].ml_dep; n0.ml_vtx = tree[t].ml_vtx; } } n0.ml_dep ++; */ } int Solve::get_maxchain() { static int queue[NVTX_MAX], depth[NVTX_MAX]; int qh = 0, qt = 1; queue[0] = 1; depth[1] = 1; int ans = 0, ansd = 1; while (qh < qt) { int v0 = queue[qh ++], d1 = depth[v0] + 1; for (int register t, i = graph[v0]; i; i = arc[i].next) if (!depth[t = arc[i].tvtx]) { queue[qt ++] = t; depth[t] = d1; if (d1 > ansd) { ansd = d1; ans = t; } } } return ans; } int main() { #ifdef STDIO Solve::solve(stdin, stdout); #else FILE *fin = fopen(INPUT, "r"), *fout = fopen(OUTPUT, "w"); Solve::solve(fin, fout); fclose(fin); fclose(fout); #endif }